本图文是Datawhale组队学习Pytorch的学习笔记，主要内容包括张量的概念（0维、1维、2维、3维、4维张量等等），自动求导的原理（通过动态图进行理解），以及对并行的理解。

第02章 Pytorch基础知识

2.1 张量

本章我们开始介绍Pytorch基础知识，我们从张量说起，建立起对数据的描述，再介绍张量的运算，最后再讲 PyTorch 中所有神经网络的核心包 autograd，也就是自动微分，了解完这些内容我们就可以较好地理解 PyTorch 代码了。下面我们开始吧～

简介

几何代数中定义的张量是基于标量、向量和矩阵的推广，比如我们可以将标量视为0维张量，向量可以视为1维张量，矩阵就是2维张量。

• 0 维张量/标量：标量是一个数字。如 1。
• 1 维张量/向量：如[1,2,3]。
• 2 维张量/矩阵：如[[1,2,3],[4,5,6]]。
• 3 维张量：如[[[1, 4, 7], [2, 5, 8]],[[1, 2, 3], [4, 5, 6]]]。

张量是现代机器学习的基础。它的核心是一个数据容器，多数情况下，它包含数字，有时候它也包含字符串，但这种情况比较少。因此可以把它想象成一个数字的水桶。

机器学习（深度学习） 中用到的数据，包括结构性数据 (数据表、序列) 和非结构性数据（图片、视屏）都是张量，总结如下：

• 数据表：2 维，形状 = (样本数，特征数)
• 序列类：3 维，形状 = (样本数，步长，特征数)
• 图像类：4 维，形状 = (样本数，宽，高，通道数)
• 视屏类：5 维，形状 = (样本数，帧数，宽，高，通道数)

机器学习，尤其深度学习，需要大量的数据，因此样本数肯定占一个维度，惯例我们把它称为维度 1。这样机器学习要处理的张量至少从 2 维开始。

2 维张量就是矩阵，也叫数据表，一般用 csv 存储。

这套表格 21,000 个数据，包括：其价格 (y)，平方英尺，卧室数，楼层，日期，翻新年份等等 21 栏。该数据形状为 (21000, 21)。传统机器学习的线性回归可以来预测房价。

2 维张量的数据表示图如下：

3 维序列数据

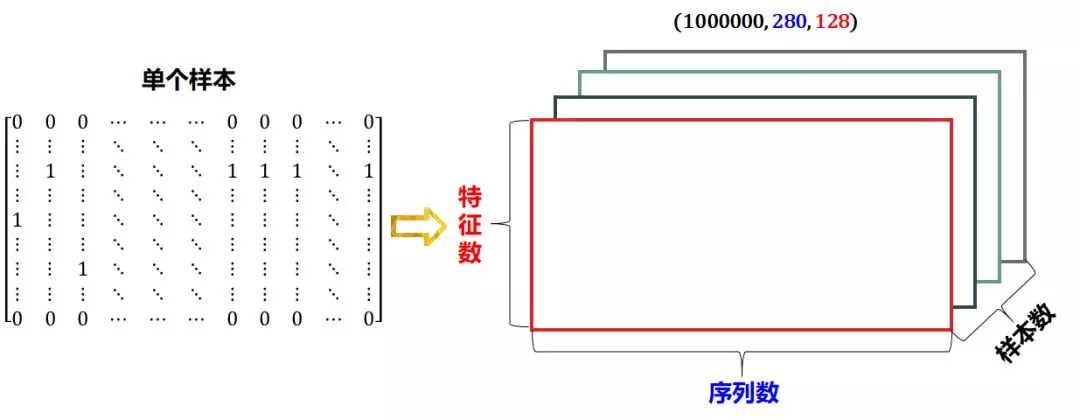
推特 (twitter) 的每条推文 (tweet) 规定只能发 280 个字符。在编码推文时，将 280 个字符的序列用独热编码 (one-hot encoding) 到包含 128 个字符的 ASCII 表，如下所示。

这样，每条推文都可以编码为 2 维张量，形状 (280, 128)，比如一条 tweet 是 “I love python 😃”，这句话映射到 ASCII 表变成：

如果收集到 1 百万条推文，那么整个数据集的形状为 (1000000, 280, 128)。传统机器学习的对率回归可以来做情感分析。

3 维张量的数据表示图如下：

?- 3维=时间序列公用数据存储在张量 时间序列数据 股价 文本数据

4维 图像数据

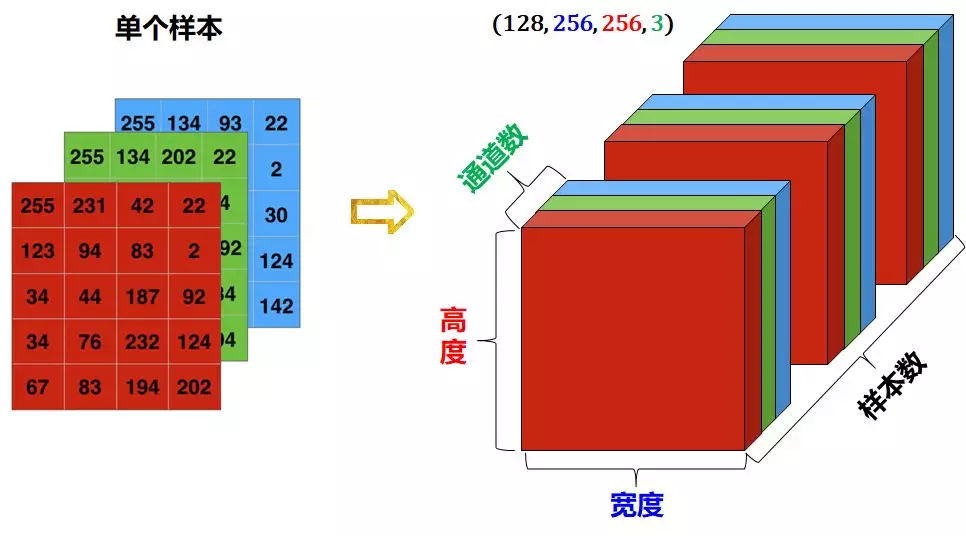
图像通常具有3个维度：宽度，高度和颜色通道。虽然是黑白图像 (如 MNIST 数字) 只有一个颜色通道，按照惯例，我们还是把它当成 3 维，即颜色通道只有一维。

• 一组黑白照片可存成形状为 (样本数，宽，高，1) 的 4 维张量
• 一组彩色照片可存成形状为 (样本数，宽，高，3) 的 4 维张量

通常 0 代表黑色，255 代表白色。

4 维张量的数据表示图如下：

5维 视频数据

视频可以被分解成一幅幅帧 (frame)。

• 每幅帧就是彩色图像，可以存储在形状是 (宽度，高度，通道) 的 3D 张量中
• 视屏 (一个序列的帧) 可以存储在形状是 (帧数，宽度，高度，通道) 的 4D 张量中
• 一批不同的视频可以存储在形状是 (样本数，帧数，宽度，高度，通道) 的 5D 张量中

下面一个 9:42 秒的 1280x720 YouTube 视频 (哈登三分绝杀勇士)，被分解成 40 个样本数据，每个样本包括 240 帧。这样的视频剪辑将存储在形状为 (40, 240, 1280, 720, 3) 的张量中。

5 维张量的数据表示图如下：

张量可以看成多维数组，下面用 Python 的numpy来定义张量。

import numpy as np# 0维张量 ()
x0 = np.array(28)# 1维张量 (3,)
x1 = np.array([1,2,3])# 2维张量 (2, 3)
x2=np.array([[1,2,3],[4,5,6]])# 3维张量 (3, 3, 4)
x3 = np.array([[[1, 4, 7, 3], [2, 5, 8, 5], [3, 6, 9, 4]],[[1, 2, 3, 4], [4, 5, 6, 3], [7, 8, 9, 5]],[[9, 8, 7, 5], [6, 5, 4, 4], [3, 2, 1, 3]]])# 4维张量 (2, 5, 4, 3)
x4 = np.ones((2,5,4,3))

不难看出：

• x0, x1, x2, x3 都是用 np.array 直接设定张量里的元素来定义张量。
• X4 用 np.ones 和张量的形状 (2,5,4,3) 来定义一个所有元素都是 1 的张量

在 PyTorch中，torch.Tensor是存储和变换数据的主要工具。如果你之前用过NumPy，你会发现Tensor和NumPy的多维数组非常类似。然而，Tensor提供GPU计算和自动求梯度等更多功能，这些使 Tensor 这一数据类型更加适合深度学习。

from __future__ import print_function
import torch

张量的操作主要包括张量的结构操作和张量的数学运算操作。

• Tensor的结构操作包括：创建张量，查看属性，修改形状，指定设备，数据转换， 索引切片，广播机制，元素操作，归并操作；
• Tensor的数学运算包括：标量运算，向量运算，矩阵操作，比较操作；

创建tensor

# （0维张量）x = torch.tensor(2)
print(x, x.shape, x.type())
# tensor(2) torch.Size([]) torch.LongTensory = torch.Tensor(2)
print(y, y.shape, y.type())
# tensor([0., 0.]) torch.Size([2]) torch.FloatTensor

注意到了torch.tensor与torch.Tensor的区别没？一字之差，结果差别却很大。

• torch.tensor(2) 返回常量2，数据类型从数据推断而来，其中的2表示的是数据值。
• torch.Tensor(2) 使用全局默认 dtype（FloatTensor），返回一个size为2的向量，初值为 0；

直接使用数据，构造一个张量：

# 1维度张量x = torch.tensor([5.5, 3])
print(x, x.shape, x.type())# tensor([5.5000, 3.0000]) torch.Size([2]) torch.FloatTensor

构造一个随机初始化的矩阵：

# 2维向量torch.manual_seed(20211013)
x = torch.rand([4, 3])
print(x, x.shape, x.type())# tensor([[0.4786, 0.4584, 0.2201],
#         [0.5064, 0.5879, 0.9110],
#         [0.8603, 0.5285, 0.0871],
#         [0.8849, 0.4521, 0.3099]]) torch.Size([4, 3]) torch.FloatTensor

构造一个矩阵全为 0，而且数据类型是 long。

# 2维向量x = torch.zeros([4,3],dtype=torch.long)
print(x)# tensor([[0, 0, 0],
#         [0, 0, 0],
#         [0, 0, 0],
#         [0, 0, 0]])

基于已经存在的 tensor，创建一个 tensor ：

x = torch.tensor([5.5, 3])
x = x.new_ones([4,3])
print(x,x.type())# tensor([[1., 1., 1.],
#         [1., 1., 1.],
#         [1., 1., 1.],
#         [1., 1., 1.]], dtype=torch.float64)# 创建一个新的tensor，返回的tensor默认具有相同的 torch.dtype和torch.device
# 也可以像之前的写法 x = torch.ones(4, 3, dtype=torch.double)x = torch.ones([4,3],dtype=torch.double)
print(x)# tensor([[1., 1., 1.],
#         [1., 1., 1.],
#         [1., 1., 1.],
#         [1., 1., 1.]], dtype=torch.float64)x = torch.rand_like(x,dtype=torch.float)
# 重置数据类型print(x)
# 结果会有一样的size
# tensor([[0.5162, 0.1575, 0.3045],
#         [0.8349, 0.5412, 0.5001],
#         [0.8255, 0.7037, 0.3061],
#         [0.4699, 0.6661, 0.0216]])

获取它的维度等属性信息：

• tensor.shape，tensor.size(): 返回张量的形状；
• tensor.ndim：查看张量的维度；
• tensor.dtype，tensor.type()：查看张量的数据类型；
• tensor.is_cuda：查看张量是否在GPU上；
• tensor.grad：查看张量的梯度；
• tensor.requires_grad：查看张量是否可微。

torch.manual_seed(20211013)
x = torch.rand([4, 3])
print("形状: ", x.shape, x.size())
print("维度: ", x.ndim)
print("类型: ", x.dtype, x.type())
print("cuda: ", x.is_cuda)
print("梯度: ", x.grad)
print("是否可微: ", x.requires_grad)# 形状:  torch.Size([4, 3]) torch.Size([4, 3])
# 维度:  2
# 类型:  torch.float32 torch.FloatTensor
# cuda:  False
# 梯度:  None
# 是否可微:  False

还有一些常见的构造Tensor的函数：

函数	功能
Tensor(*sizes)	基础构造函数。 直接从参数构建一个张量，支持List，Numpy数组。
tensor(data)	类似于np.array
ones(*sizes)	指定shape，生成元素全1的数据。
zeros(*sizes)	指定shape，生成元素全0的数据。
eye(*sizes)	对角为1，其余为0。 指定（行列）数，创建二维单位Tensor。
arange(s,e,step)	从s到e，步长为step生成一个序列张量。
linspace(s,e,steps)	从s到e，均匀分成step份。
logspace(s,e,steps)	从10^s 到 10^e，均匀分成steps份。
rand/randn(*sizes)	生成[0,1]均匀分布和标准正态分布数据。
normal(mean,std)/uniform(from,to)	正态分布/均匀分布
randperm(m)	随机排列

操作

一些加法操作：

torch.manual_seed(20211013)
x = torch.rand([4, 3])
y = torch.ones([4, 3])
print(x)
# tensor([[0.4786, 0.4584, 0.2201],
#         [0.5064, 0.5879, 0.9110],
#         [0.8603, 0.5285, 0.0871],
#         [0.8849, 0.4521, 0.3099]])# 方式1
print(x + y)
# tensor([[1.4786, 1.4584, 1.2201],
#         [1.5064, 1.5879, 1.9110],
#         [1.8603, 1.5285, 1.0871],
#         [1.8849, 1.4521, 1.3099]])# 方式2
print(torch.add(x, y))
# tensor([[1.4786, 1.4584, 1.2201],
#         [1.5064, 1.5879, 1.9110],
#         [1.8603, 1.5285, 1.0871],
#         [1.8849, 1.4521, 1.3099]])# 方式3 提供一个输出 tensor 作为参数
result = torch.empty([4, 3])
torch.add(x, y, out=result)
print(result)
# tensor([[1.4786, 1.4584, 1.2201],
#         [1.5064, 1.5879, 1.9110],
#         [1.8603, 1.5285, 1.0871],
#         [1.8849, 1.4521, 1.3099]])# 方式4 in-place
y.add_(x)
print(y)
# tensor([[1.4786, 1.4584, 1.2201],
#         [1.5064, 1.5879, 1.9110],
#         [1.8603, 1.5285, 1.0871],
#         [1.8849, 1.4521, 1.3099]])

索引操作：（类似于numpy）

需要注意的是：索引出来的结果与原数据共享内存，也即修改一个，另一个会跟着修改。

torch.manual_seed(20211013)
x = torch.rand([4, 3])
print(x)
# tensor([[0.4786, 0.4584, 0.2201],
#         [0.5064, 0.5879, 0.9110],
#         [0.8603, 0.5285, 0.0871],
#         [0.8849, 0.4521, 0.3099]])# 取第二列
print(x[:, 1])
# tensor([0.4584, 0.5879, 0.5285, 0.4521])

y = x[0, :]
y += 1
print(y)
# tensor([1.4786, 1.4584, 1.2201])print(x[0, :])
# tensor([1.4786, 1.4584, 1.2201]) # 源tensor也被改了了

改变大小：如果你想改变一个 tensor 的大小或者形状，你可以使用 torch.view：

torch.manual_seed(20211013)
x = torch.randn([4, 4])
print(x)
# tensor([[ 0.9747,  0.8300, -0.6734, -0.4365],
#         [ 0.1867,  0.9543,  0.3457, -0.1776],
#         [ 0.5936, -0.7330,  0.2092,  1.1053],
#         [ 1.3183, -1.9817,  1.9537, -1.2133]])y = x.view(16)
z = x.view(-1, 8) # -1是指这一维的维数由其他维度决定
print(x.size(), y.size(), z.size())
# torch.Size([4, 4]) torch.Size([16]) torch.Size([2, 8])print(y)
# tensor([ 0.9747,  0.8300, -0.6734, -0.4365,  0.1867,  0.9543,  0.3457, -0.1776,
#          0.5936, -0.7330,  0.2092,  1.1053,  1.3183, -1.9817,  1.9537, -1.2133])print(z)
# tensor([[ 0.9747,  0.8300, -0.6734, -0.4365,  0.1867,  0.9543,  0.3457, -0.1776],
#         [ 0.5936, -0.7330,  0.2092,  1.1053,  1.3183, -1.9817,  1.9537, -1.2133]])

注意 view() 返回的新tensor与源tensor共享内存（其实是同一个tensor），也即更改其中的一个，另外一个也会跟着改变。（顾名思义，view仅仅是改变了对这个张量的观察⻆度）。

x += 1
print(x)
# tensor([[ 1.9747,  1.8300,  0.3266,  0.5635],
#         [ 1.1867,  1.9543,  1.3457,  0.8224],
#         [ 1.5936,  0.2670,  1.2092,  2.1053],
#         [ 2.3183, -0.9817,  2.9537, -0.2133]])print(y) # 也加了了1
# tensor([ 1.9747,  1.8300,  0.3266,  0.5635,  1.1867,  1.9543,  1.3457,  0.8224,
#          1.5936,  0.2670,  1.2092,  2.1053,  2.3183, -0.9817,  2.9537, -0.2133])

所以如果我们想返回一个真正新的副本（即不共享内存）该怎么办呢？

Pytorch还提供了一 个reshape()可以改变形状，但是此函数并不能保证返回的是其拷贝，所以不推荐使用。推荐先用clone创造一个副本然后再使用view。

注意：使用clone还有一个好处是会被记录在计算图中，即梯度回传到副本时也会传到源 Tensor 。

如果你有一个元素 tensor ，使用 .item() 来获得这个 value，即得到Python的标量：

x = torch.randn(1)
print(x)
# tensor([0.1032])
print(x.item())
# 0.10324124991893768

PyTorch中的 Tensor 支持超过一百种操作，包括转置、索引、切片、数学运算、线性代数、随机数等等，可参考官方文档。

广播机制

当对两个形状不同的 Tensor 按元素运算时，可能会触发广播（broadcasting）机制：先适当复制元素使这两个 Tensor 形状相同后再按元素运算。

import torchx = torch.arange(1, 3).view(1, 2)
print(x)
# tensor([1, 2])y = torch.arange(1, 4).view(3, 1)
print(y)
# tensor([[1],
#         [2],
#         [3]])print(x + y)
# tensor([[2, 3],
#         [3, 4],
#         [4, 5]])

由于 x 和 y 分别是1行2列和3行1列的矩阵，如果要计算 x + y ，那么 x 中第一行的2个元素被广播（复制）到了第二行和第三行，y中第1列的3个元素被广播（复制）到了第二列。如此，就可以对2 个3行2列的矩阵按元素相加。

2.2 自动求导

PyTorch 中，所有神经网络的核心是autograd包。autograd包为张量上的所有操作提供了自动求导机制。它是一个在运行时定义（define-by-run）的框架，这意味着反向传播是根据代码如何运行来决定的，并且每次迭代可以是不同的。

torch.Tensor是这个包的核心类。如果设置它的属性.requires_grad为True，那么它将会追踪对于该张量的所有操作。当完成计算后可以通过调用.backward()，来自动计算所有的梯度。这个张量的所有梯度将会自动累加到.grad属性。

注意：在y.backward()时，如果 y 是标量，则不需要为backward()传入任何参数；否则，需要传入一个与 y 同形的Tensor。

要阻止一个张量被跟踪历史，可以调用.detach()方法将其与计算历史分离，并阻止它未来的计算记录被跟踪。为了防止跟踪历史记录（和使用内存），可以将代码块包装在 with torch.no_grad():中。在评估模型时特别有用，因为模型可能具有requires_grad = True 的可训练的参数，但是我们不需要在此过程中对他们进行梯度计算。

还有一个类对于autograd的实现非常重要：Function。Tensor和Function互相连接生成了一个无环图（acyclic graph），它编码了完整的计算历史。每个张量都有一个.grad_fn属性，该属性引用了创建 Tensor自身的Function（除非这个张量是用户手动创建的，即这个张量的grad_fn是None）。

如果需要计算导数，可以在 Tensor 上调用 .backward()。如果Tensor 是一个标量（即它包含一个元素的数据），则不需要为backward()指定任何参数，但是如果它有更多的元素，则需要指定一个gradient参数，该参数是形状匹配的张量。

import torch

创建一个张量并设置requires_grad=True用来追踪其计算历史。

x = torch.ones([2, 2], requires_grad=True)
print(x)
# tensor([[1., 1.],
#         [1., 1.]], requires_grad=True)

对这个张量做一次运算：

y = x ** 2
print(y)
# tensor([[1., 1.],
#         [1., 1.]], grad_fn=<PowBackward0>)

y是计算的结果，所以它有grad_fn属性。

print(y.grad_fn)
# <PowBackward0 object at 0x000000600D5E1D30>

对y进行更多操作

z = y * y * 3
print(z)
# tensor([[3., 3.],
#         [3., 3.]], grad_fn=<MulBackward0>)out = z.mean()
print(out)
# tensor(3., grad_fn=<MeanBackward0>)

.requires_grad_(...)原地改变了现有张量的requires_grad标志。如果没有指定的话，默认输入的这个标志是False。

torch.manual_seed(20211013)
a = torch.rand(2, 2)  # 缺失情况下默认 requires_grad = False
a = ((a * 3) / (a - 1))
print(a.requires_grad)  # Falsea.requires_grad_(True)
print(a.requires_grad)  # Trueb = (a * a).sum()
print(b.grad_fn)
# <SumBackward0 object at 0x000000A46BEC1D30>

梯度

现在开始进行反向传播，因为out是一个标量，因此out.backward()和out.backward(torch.tensor(1.))等价。

输出导数d(out)/dx

x = torch.ones([2, 2], requires_grad=True)
y = x ** 2
z = y * y * 3
out = z.mean()
out.backward()print(x.grad)
# tensor([[3., 3.],
#         [3., 3.]])

数学上，若有向量函数$\vec{y}=f(\vec{x})$，那么 $\vec{y}$ 关于 $\vec{x}$
的梯度就是一个雅可比矩阵：

J=\left(\begin{array}{ccc}\frac{\partial y_{1}}{\partial x_{1}} & \cdots & \frac{\partial y_{1}}{\partial x_{n}} \\ \vdots & \ddots & \vdots \\ \frac{\partial y_{m}}{\partial x_{1}} & \cdots & \frac{\partial y_{m}}{\partial x_{n}}\end{array}\right)

而 torch.autograd 这个包就是用来计算一些雅可比矩阵的乘积的。例如，如果$v$是一个标量函数$l = g(\vec{y})$的梯度：

v=\left(\begin{array}{lll}\frac{\partial l}{\partial y_{1}} & \cdots & \frac{\partial l}{\partial y_{m}}\end{array}\right)

由链式法则，我们可以得到：

v J=\left(\begin{array}{lll}\frac{\partial l}{\partial y_{1}} & \cdots & \frac{\partial l}{\partial y_{m}}\end{array}\right)\left(\begin{array}{ccc}\frac{\partial y_{1}}{\partial x_{1}} & \cdots & \frac{\partial y_{1}}{\partial x_{n}} \\ \vdots & \ddots & \vdots \\ \frac{\partial y_{m}}{\partial x_{1}} & \cdots & \frac{\partial y_{m}}{\partial x_{n}}\end{array}\right)=\left(\begin{array}{lll}\frac{\partial l}{\partial x_{1}} & \cdots & \frac{\partial l}{\partial x_{n}}\end{array}\right)

注意：grad在反向传播过程中是累加的（accumulated），这意味着每一次运行反向传播，梯度都会累加之前的梯度，所以一般在反向传播之前需把梯度清零。

# 再来反向传播一次，注意grad是累加的 2 out2 = x.sum()
out2 = x.sum()
out2.backward()
print(x.grad)
# tensor([[4., 4.],
#         [4., 4.]])out3 = x.sum()
x.grad.data.zero_()
out3.backward()
print(x.grad)
# tensor([[1., 1.],
#         [1., 1.]])

现在我们来看一个雅可比向量积的例子：

torch.manual_seed(20211013)
x = torch.randn(3, requires_grad=True)
print(x)
# tensor([ 0.8004, -1.4908, -0.6038], requires_grad=True)y = x * 2
i = 0
while y.data.norm() < 1000:y = y * 2i = i + 1
print(y)
# tensor([  819.6005, -1526.5718,  -618.2654], grad_fn=<MulBackward0>)
print(i)
# 9

在这种情况下，y不再是标量。torch.autograd不能直接计算完整的雅可比矩阵，但是如果我们只想要雅可比向量积，只需将这个向量作为参数传给backward：

torch.manual_seed(20211013)
x = torch.randn(3, requires_grad=True)
print(x)
# tensor([ 0.8004, -1.4908, -0.6038], requires_grad=True)
y = x * 2
print(y)
# tensor([ 1.6008, -2.9816, -1.2075], grad_fn=<MulBackward0>)
y.backward()
# RuntimeError: grad can be implicitly created only for scalar outputs
print(x.grad)

v = torch.tensor([0.1, 1.0, 0.0001], dtype=torch.float)
y.backward(v)
print(x.grad)
# tensor([1.0240e+02, 1.0240e+03, 1.0240e-01])

也可以通过将代码块包装在with torch.no_grad(): 中，来阻止autograd跟踪设置了.requires_grad=True的张量的历史记录。

torch.manual_seed(20211013)
x = torch.randn(3, requires_grad=True)
print(x.requires_grad)  # True
print((x ** 2).requires_grad)  # Truewith torch.no_grad():print((x ** 2).requires_grad)  # False

如果我们想要修改 tensor 的数值，但是又不希望被 autograd 记录（即不会影响反向传播）， 那么我么可以对 tensor.data 进行操作。

x = torch.ones(1,requires_grad=True)print(x.data) # 还是一个tensor
# tensor([1.])print(x.data.requires_grad) # 但是已经是独立于计算图之外
# Falsey = 2 * x
x.data *= 100 # 只改变了值，不会记录在计算图，所以不会影响梯度传播
y.backward()
print(x) # 更改data的值也会影响tensor的值 
# tensor([100.], requires_grad=True)print(x.grad)
# tensor([2.])

2.3 并行计算简介

在利用PyTorch做深度学习的过程中，可能会遇到数据量较大无法在单块GPU上完成，或者需要提升计算速度的场景，这时就需要用到并行计算。本节让我们来简单地了解一下并行计算的基本概念和主要实现方式，具体的内容会在课程的第二部分详细介绍。

2.3.1 为什么要做并行计算

我们学习PyTorch的目的就是可以编写我们自己的框架，来完成特定的任务。可以说，在深度学习时代，GPU的出现让我们可以训练的更快，更好。所以，如何充分利用GPU的性能来提高我们模型学习的效果，这一技能是我们必须要学习的。这一节，我们主要讲的就是PyTorch的并行计算。PyTorch可以在编写完模型之后，让多个GPU来参与训练。

2.3.2 CUDA是个啥

CUDA是我们使用GPU的提供商——NVIDIA提供的GPU并行计算框架。对于GPU本身的编程，使用的是CUDA语言来实现的。但是，在我们使用PyTorch编写深度学习代码时，使用的CUDA又是另一个意思。在PyTorch使用 CUDA表示要开始要求我们的模型或者数据开始使用GPU了。

在编写程序中，当我们使用了 cuda() 时，其功能是让我们的模型或者数据迁移到GPU当中，通过GPU开始计算。

2.3.3 做并行的方法

• 网络结构分布到不同的设备中(Network partitioning)

在刚开始做模型并行的时候，这个方案使用的比较多。其中主要的思路是，将一个模型的各个部分拆分，然后将不同的部分放入到GPU来做不同任务的计算。其架构如下：

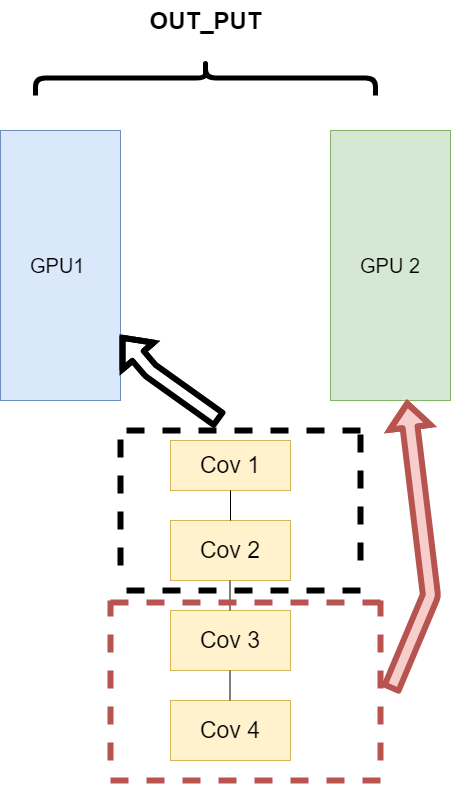
这里遇到的问题就是，不同模型组件在不同的GPU上时，GPU之间的传输就很重要，对于GPU之间的通信是一个考验。但是GPU的通信在这种密集任务中很难办到。所有这个方式慢慢淡出了视野，

• 同一层的任务分布到不同数据中(Layer-wise partitioning)

第二种方式就是，同一层的模型做一个拆分，让不同的GPU去训练同一层模型的部分任务。其架构如下：

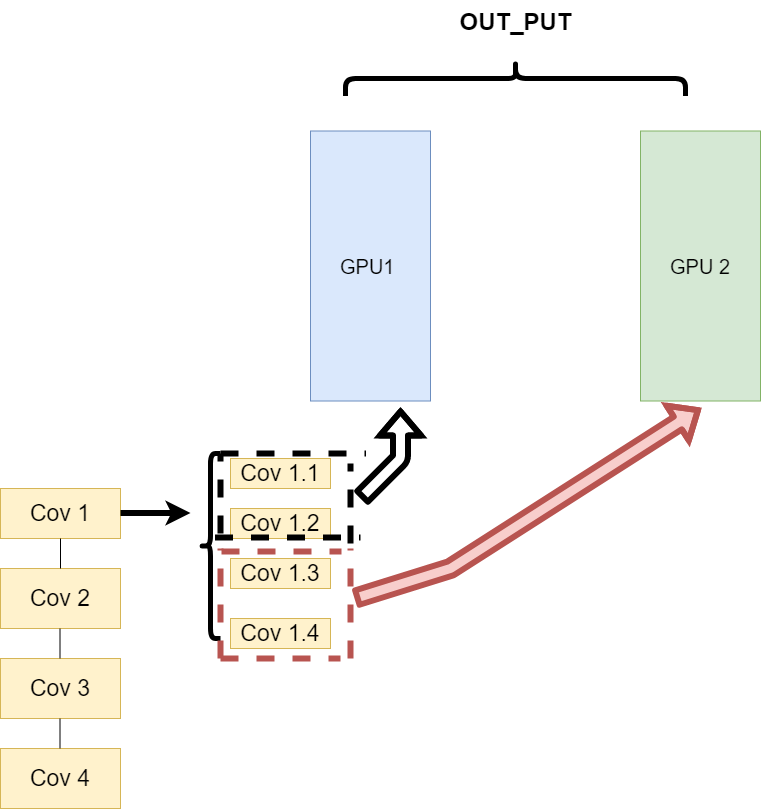
这样可以保证在不同组件之间传输的问题，但是在我们需要大量的训练，同步任务加重的情况下，会出现和第一种方式一样的问题。

• 不同的数据分布到不同的设备中，执行相同的任务(Data parallelism)

第三种方式有点不一样，它的逻辑是，我不再拆分模型，我训练的时候模型都是一整个模型。但是我将输入的数据拆分。所谓的拆分数据就是，同一个模型在不同GPU中训练一部分数据，然后再分别计算一部分数据之后，只需要将输出的数据做一个汇总，然后再反传。其架构如下：

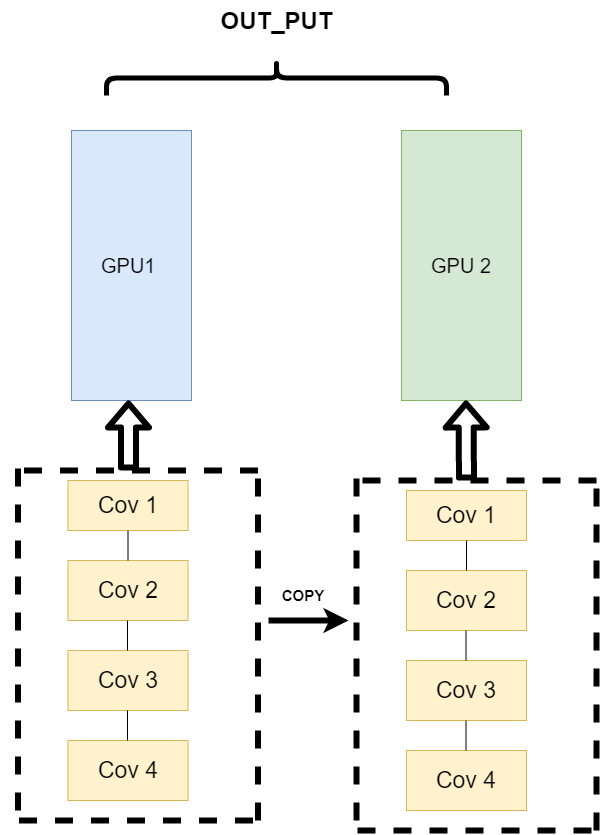
这种方式可以解决之前模式遇到的通讯问题。

PS:现在的主流方式是数据并行的方式（Data parallelism）

---

补充：通过股票数据感受张量概念。

在量化金融中，我们用股票数据举例来说明不同维度的张量。

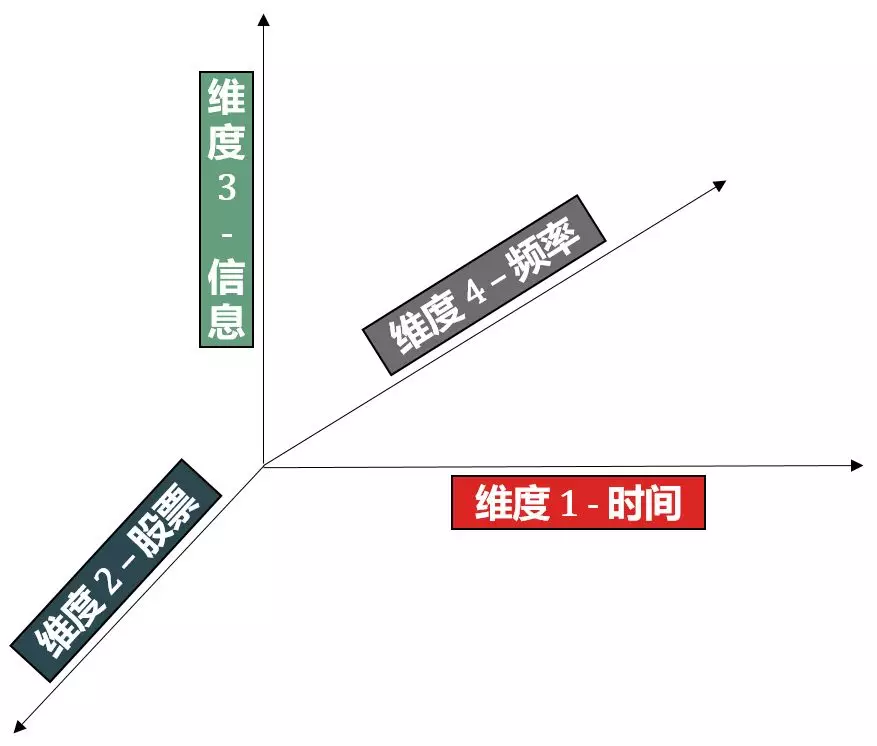
阶段一：一个收盘价

斯蒂文查了查 2019 年 1 月 3 日平安银行 (000001.XSHE) 的收盘价，发现是 9.28，他默默将这个单数字存到 X0 里。

X0 又称为标量 (scalar)，或更严谨的称为 0 维张量 (0D tensor)。

阶段二：加入时间维度

单天股票价格太少，至少要算一些均值、标准差这些统计量吧。

斯蒂文从一天的数据扩展到一年，下载了从 2019 年 1 月 3 日起过去一年的平安银行历史收盘价，存到 X1 里。

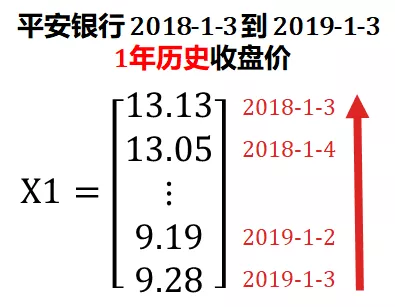
X1 在 X0 基础上添加了时间维度 （红色箭头），从标量扩展成向量 (vector)，又称为 1 维张量 (1D tensor)。

阶段三：加入股票维度

单个股票太少，分散原则告诉我们需要投资相关性系数为负的两支股票。

斯蒂文增加了茅台股票 (600519.XSHG)，下载了从 2019年 1 月 3 日起过去一年的平安银行和茅台历史收盘价，存到 X2 里。

X2 在 X1 基础上添加了横截维度（蓝色箭头），从向量扩展成矩阵（matrix），又称为 2 维张量（2D tensor）。

阶段四：加入信息维度

收盘价一个信息不够，在趋势追踪模型中，价格和交易量是在股票走势中相当重要的因素。

斯蒂文增加了交易量，下载了从 2019 年 1 月 3 日起过去一年的平安银行和茅台历史收盘价和交易量，存到 X3 里。

X3 在 X2 基础上添加了信息维度（绿色箭头），从矩阵扩展成 3 维张量（3D tensor）。

阶段五：加入频率维度

收盘信息太过于少，如果要日内交易怎么办？

斯蒂文又增加了 tick 数据，下载了从 2019 年 1 月 3 日起过去一年的平安银行和茅台历史 tick 价格和交易量，存到 X4 里。

国外和国内对于 tick 数据定义有些不同：

• 国外：任何委托单（order）使委托账本（order book）变化而得到的表格。
• 国内：对委托账本的按一定切片时间（500 毫秒，3 秒，6 秒等）抽样的信息。

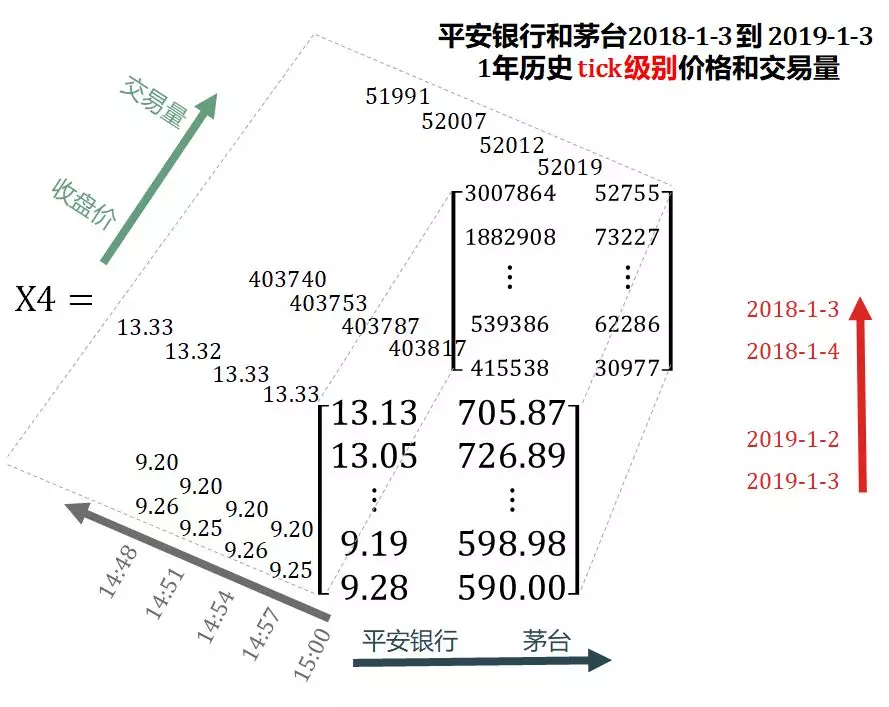
X4 在 X3 基础上添加了频率维度(灰色箭头)，从 3 维张量扩展成 4 维张量 (4D tensor)。