论文阅读报告

0 2022/6/23-2022/6/25

1. FLAME: Taming Backdoors in Federated Learning

1.1 本文的贡献

我们提出了FLAME，这是一种针对FL中后门攻击的防御框架，能够消除后门而不影响聚合模型的良性性能。与早期的后门防御相反，FLAME适用于一般对手模型，即它不依赖于对手攻击策略的有力假设，也不依赖于良性和敌对数据集的底层数据分布。
我们表明，通过以下方法可以从根本上减少所需的高斯噪声：a）应用我们的聚类方法来删除潜在的恶意模型更新，b）将局部模型的权重裁剪到适当的水平，以限制单个（尤其是恶意）模型对聚合模型的影响。
我们为噪声注入（受DP启发）所需的高斯噪声量提供了噪声边界证明，以消除后门贡献。
我们对来自三个非常不同的应用领域的真实世界数据集的防御框架进行了广泛的评估。我们表明，FLAME减少了所需的噪声量，因此聚合模型的良性性能不会显著降低，与直接注入基于DP的噪声的最先进防御相比，它具有重要的优势。

1.2 问题设置和目标

后门特征描述：
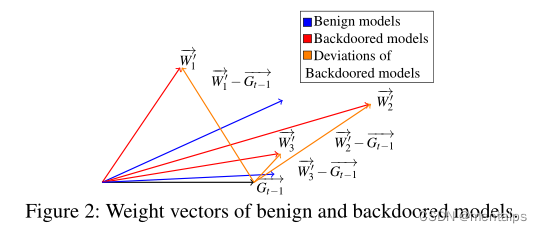
在这里插入图片描述
Benign models:良性模型；
Backdoored models:后门攻击模型；
Deviations of Backdoored models：后门模型的偏差；
$G_{t-1}$ :上一轮局部模型；
$W_{1}^{,},W_{2}^{,},W_{3}^{,},$ :分别代表三种不同的后门攻击；
防御目标：
在FL环境下，能够有效缓解后门攻击的通用防御需要实现以下目标：（i）有效性：为了防止对手实现其攻击目标，必须消除后门模型更新的影响，以便聚合的全局模型不会显示后门行为。（ii）性能：必须保持全局模型的良性性能，以保持其效用。（iii）独立于数据分布和攻击策略：防御方法必须适用于一般对手模型，即不得要求事先了解后门攻击方法，或对本地客户端的特定数据分布作出假设，例如，数据是iid还是非iid。

1.2 FLAME概述和设计

动机：
早期的工作使用聚合模型的差异隐私启发噪声消除后门。它们确定了根据经验使用的足够数量的噪声。然而，在FL设置中，这是一个挑战，因为通常不能假设聚合器可以访问训练数据，尤其是有毒数据集。因此，需要一种通用方法来确定多少噪声足以有效地移除后门。另一方面，模型中注入的噪声越多，对其良性性能的影响就越大。
FLAME概述：
FLAME估计了在FL环境中后门拆除所需的噪声级，无需进行广泛的经验评估，也无需获取培训数据。此外，为了有效限制所需的噪声量，FLAME使用一种新的基于聚类的方法来识别和删除影响较大的对手模型更新，并应用动态权重裁剪方法来限制对手为提高性能而扩大的模型的影响。如§3所述，我们无法保证所有后门模型都能被检测到，因为对手可以完全控制角度和幅度偏差，使模型任意难以检测。因此，我们的聚类方法旨在删除具有高攻击影响（角度偏差较大）的模型，而不是所有恶意模型。图3说明了由上述三个组件组成的FLAME的高级概念：过滤、剪裁和噪声。然而，我们强调，这些组件中的每一个都需要非常小心地应用，因为噪声与聚类和剪裁的天真结合会导致不良结果，因为它很容易无法缓解后门和/或恶化模型的良性性能。
FLAME设计：
在这里插入图片描述

FLAME使用成对余弦距离来测量所有模型更新之间的角度差，并应用HDBSCAN聚类算法。这里的优点是，即使对手放大模型更新以增强其影响，余弦距离也不会受到影响，因为这不会改变更新权重向量之间的角度。由于HDBSCAN算法根据余弦距离分布的密度对模型进行聚类，并动态确定所需的聚类数。
步骤：
1.服务器获取n个用户的模型。
2.计算 $n$ 个模型两两之间的余弦相似度。
3.使用动态聚类算法HDBSCAN对两两之间的余弦相似度进行聚类，超过50 % 的类为良性更新。其他类均视为离群值，将其剔除，得到剩余的 $L$ 个良性模型。
4.对 $n$ 个模型中的每个模型计算和当前全局模型的欧式距离 $e_{1},e_{2},...,e_{n})$ ，并令其中值为 $S_{t}$ 。
5.对于每一轮的 $L$ 个用聚类算法筛选出来的模型，令其动态自适应剪裁阈值为 $\gamma=S_{t}/e_{l}$ 。
6.计算剪裁后的局部模型 $W_{l}=G_{t-1}+(W_{l}-G_{t-1})*MIN(1,\gamma)$ 。
7.对剪裁后的局部模型赋予相同的权重进行聚合得到全局模型 $G_{t}$ 。
8.基于局部模型之间的差异（距离）得到动态自适应噪声量 $\sigma=\lambda*S_{t}$ ，其中超参数 $\lambda$ 是根据经验设置的噪声水平因子。
9.得到加噪后的全局模型 $G_{t}=G_{t}+N(0,\sigma^{2})$ 。