Dropout技术之随机神经元与随机深度

1. 写在前面

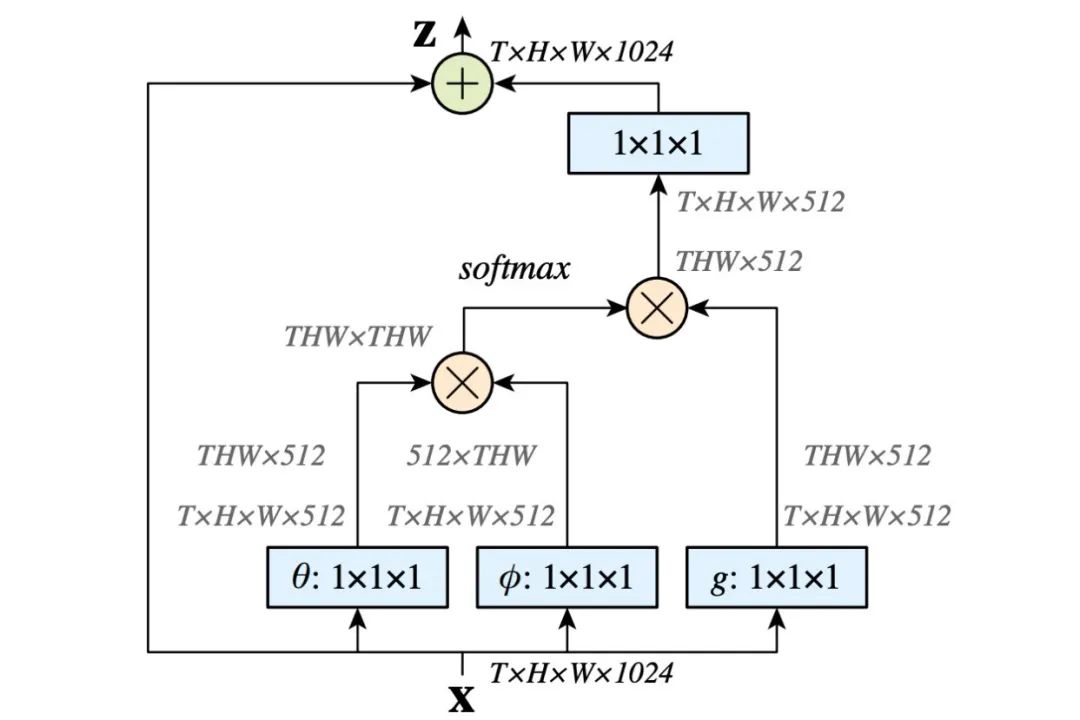
在学习复现EfficientNet网络的时候，里面有一个MBConv模块长下面这个样子：

在这里插入图片描述
当然，这个结构本身并不是很新奇，从resNet开始，几乎后面很多网络，比如DenseNet， MobileNet系列，ShuffleNet系列以及EfficientNet系列都会发现这样的残差结构。但这次探索里面发现了Dropout这个点，之前在实现残差结构的时候，如果碰到Dropout，我一直以为是之前学习到的随机失活神经元的Dropout，但直到在这里看到源码才发现，不是我想象的那么简单！

这种残差结构里面使用的Dropout，是一种叫做随机深度的Dropout技术。这个是2016年ECCV上发表的一篇paper，论文叫做《Deep Network with Stochastic depth》，说的是训练过程中，不是随机失活每一层的神经元了，而是随机去掉很多层，这样能减少冗余，还能加速训练。

出于好奇，我读了下这篇paper，又学习到了一种训练带有残差网络的骚操作，所以，这篇文章想统一把这两种Dropout放一块整理下。

2. Dropout之随机神经元

这个技术就是普通的Dropout技术了，Dropout随机失活神经元，就是我们给出一个概率，让神经网络层的某个神经元权重为0(失活)

就是每一层，让某些神经元不起作用，这样就就相当于把网络进行简化了(左边和右边可以对比），我们有时候之所以会出现过拟合现象，就是因为我们的网络太复杂了，参数太多了，并且我们后面层的网络也可能太过于依赖前层的某个神经元。

加入Dropout之后，首先网络会变得简单，减少一些参数，并且由于不知道浅层的哪些神经元会失活，导致后面的网络不敢放太多的权重在前层的某个神经元，这样就减轻了一个过渡依赖的现象，对特征少了依赖，从而有利于缓解过拟合。

这个类似于我们期末考试的时候有没有，老师总是会给我们画出一个重点，但是由于我们不知道这些重点哪些会真的出现在试卷上，所以就得把精力分的均匀一些，都得看看，这样保险一些，也能泛化一点，至少只要是这些类型的题都会做。而如果我们不把精力分的均匀一些，只关注某种题型，那么准糊一波

所以这种Dropout技术可以帮助网络缓解过拟合。不太难理解，但使用的时候有几个注意问题：

数据尺度变化
我们用Dropout的时候是这样用的： 只在训练的时候开启Dropout，而测试的时候是不用Dropout的，也就是说模型训练的时候会随机失活一部分神经元，而测试的时候我们用所有的神经元，那么这时候就会出现这个数据尺度的问题，所以测试的时候，所有权重都乘以1-drop_prob，以保证训练和测试时尺度变化一致。怎么理解？依然拿上面的图来说：

假设我们的输入是100个特征，那么第一层的第一个神经元的表达式应该是这样，这里先假设不失活：
$Z_{1}^{1}=\sum_{i=1}^{100} w_{i} x_{i}$
假设我们这里的 $w_ix_i=1$ ，那么第一层第1个神经元 $Z_1^1=100$ ，注意这是不失活的情况，那么如果失活呢？假设失活率drop_prob=0.3，也就是我们的输入大约有30%是不起作用的，也就是会有30个不起作用，当然这里是大约哈，因为失活率%30指的是每个神经元的失活率。换在整体上差不多可以理解成30个不起作用，那么我们的 $Z_1^1$ 相当于
${Z_1^1}_{train} = \sum_{i=1}^{70} w_ix_i = 70$
我们发现，如果使用Dropout之后，我们的 $Z_1^1$ 成了70，比起不失活来少了30，这就是一个尺度的变化，所以我们就发现如果训练的时候用Dropout，我们每个神经元取值的一个尺度是会缩小的，比如这里的70，而测试的时候我们用的是全部的神经元，尺度会变成100，这就导致了模型在数值上有了一个差异。因此，我们在测试的时候，需要所有的权重乘以1-drop_prob这一项，这时候我们在测试的时候就相当于：
${Z_1^1}_{test} = \sum_{i=1}^{100}(0.7\times w_i)x_i = 0.7 \times100 = 70$

这样采用Dropout的训练集和不采用Dropout的测试集的尺度就变成一致了。 Pytorch在实现Dropout的时候，是权重乘以 $\frac{1}{1-p}$ 的，也就是除以1-p, 这样就不用再测试的时候权重乘以1-p了，也没有改变原来数据的尺度。 也就是上面公式中的
${Z_1^1}_{train} = \sum_{i=1}^{70} (\frac{70}{0.7}w_i)x_i = 100 \\ {Z_1^1}_{test} = \sum_{i=1}^{100} w_ix_i = 100$
这个细节要注意下。

Dropout层放置的位置
比如，我们写下面这段代码

class MLP(nn.Module):def __init__(self, neural_num, d_prob=0.5):super(MLP, self).__init__()self.linears = nn.Sequential(nn.Linear(1, neural_num),nn.ReLU(inplace=True),nn.Dropout(d_prob),             # 注意这里用上了Dropout， 我们看到这个Dropout是接在第二个Linear之前，Dropout通常放在需要Dropout网络的前一层nn.Linear(neural_num, neural_num),nn.ReLU(inplace=True),nn.Dropout(d_prob),nn.Linear(neural_num, neural_num),nn.ReLU(inplace=True),nn.Dropout(d_prob),  # 通常输出层的Dropout是不加的，这里由于数据太简单了才加上nn.Linear(neural_num, 1),)def forward(self, x):return self.linears(x)net_prob_05 = MLP(neural_num=n_hidden, d_prob=0.5)# ============================ step 3/5 优化器 ============================
optim_reglar = torch.optim.SGD(net_prob_05.parameters(), lr=lr_init, momentum=0.9)# ============================ step 4/5 损失函数 ============================
loss_func = torch.nn.MSELoss()# ============================ step 5/5 迭代训练 ============================for epoch in range(max_iter):pred_wdecay = net_prob_05(train_x)loss_wdecay = loss_func(pred_wdecay, train_y)optim_reglar.zero_grad(）loss_wdecay.backward()optim_reglar.step()if (epoch+1) % disp_interval == 0:# 这里要注意一下，Dropout在训练和测试阶段不一样，这时候需要对网络设置一个状态net_prob_05.eval() # 这个.eval()函数表示我们的网络即将使用测试状态， 设置了这个测试状态之后，才能用测试数据去测试网络， 否则网络怎么知道啥时候测试啥时候训练？test_pred_prob_05 = net_prob_05(test_x)

这里注意看MLP网络里面Dropout层的位置，一般是放在需要Dropout的层的前面。输入层不需要dropout，最后一个输出层一般也不需要。就是由于Dropout操作，模型训练和测试是不一样的，上面我们说了，训练的时候采用Dropout而测试的时候不用Dropout，那么我们在迭代的时候，就得告诉网络目前是什么状态，如果要测试，就得先用.eval()函数告诉网络一下子，训练的时候就用.train()函数告诉网络一下子。

这就是我们之前熟知的Dropout随机神经元技术了，之前我的学习认知也停留在这里为止，直到又见识到了随机深度技术，所以下面重点整理下这个是怎么玩的。

3. Dropout之随机深度

随机深度是黄高博士在2016年提出来的一种针对网络高效训练的技术，谈到黄高博士，可能大家更熟悉他提出的DenseNet网络，这个网络要比随机深度晚一些，但也受到随机深度的一些启发。

3.1 背景

深的网络在现在表现出了十分强大的能力，但是也存在许多问题。即使在现代计算机上，梯度会消散、前向传播中信息的不断衰减、训练时间也会非常缓慢等问题。

ResNet的强大性能在很多应用中已经得到了证实，尽管如此，ResNet还是有一个不可忽视的缺陷——更深层的网络通常需要进行数周的训练——因此，把它应用在实际场景下的成本非常高。为了解决这个问题，作者们引入了一个“反直觉”的方法，即在我们可以在训练过程中任意地丢弃一些层，并在测试过程中使用完整的网络。

在EfficientNet中也逐渐发现了这个现象，之前的一些研究，主要是关注网络的准确率和参数数量，比如设计更加复杂的网络结构，更深，更宽，分辨率更大等，去提高网络的准确率，但后来逐渐发现，这些网络在实际场景中可能不太好落地。所以后续的一些研究，又开始关注与网络的训练速度，推理速度等，所以一些轻量级的网络慢慢诞生。比如MobileNet系列，ShuffleNet系列以及EfficientNet系列。当然也有可能是精度慢慢的到了瓶颈了。

这篇paper也是想提高网络的训练速度或者效率，所以思路就是提出随机深度，在训练时使用较浅的深度(随机在resnet的基础上pass掉一些层)，在测试时使用较深的深度，较少训练时间，提高训练性能，最终在四个数据集上都超过了resnet原有的性能(cifar-10, cifar-100, SVHN, imageNet)。其训练过程中采用随机dropout一些中间层的方法改进ResNet，发现可以显著提高ResNet的泛化能力。

那么怎么做到呢？

3.2 网络基本思想

作者用了残差块作为他们网络的构件，因此，在训练中，如果一个特定的残差块被启用了，那么它的输入就会同时流经恒等表换shortcut（identity shortcut）和权重层；否则输入就只会流经恒等变换shortcut。

在训练的过程中，每一个层都有一个“生存概率”，并且都会被任意丢弃。在测试过程中，所有的block都将保持被激活状态，而且block都将根据其在训练中的生存概率进行调整。

在这里插入图片描述
假设 $H_l$ 是第 $l$ 个残差块的输出结果， $f_l$ 是由第 $l$ 个残差块的主分支输出。 $b_l$ 是一个随机变量(只有1或者0，反映一个block是否是被激活的，或者是否启用当前主分支)。那么加了随机深度的Dropout之后的残差块输出公式计算如下：
$H_{\ell}=\operatorname{ReLU}\left(b_{\ell} f_{\ell}\left(H_{\ell-1}\right)+\operatorname{id}\left(H_{\ell-1}\right)\right)$
这个其实也非常好理解，原先的残差结构，就是跳远连接+主分支然后非线性激活，只不过这里多了一个 $b_l$ 来控制主分支是否有效。如果 $b_l=0$ ，那么
$H_{l}=\operatorname{ReLU}\left(i d\left(H_{l-1}\right)\right)$
直走跳远连接，而这个是恒等映射，相当于当前的残差块不起作用，否则当前的残差块就被启用。

那么这个 $b_l$ 是怎么得到的呢？这个和普通Dropout差不多，我们对于每个残差块，都指定一个是主分支激活的概率 $p$ ，即每个残差块都有 $1 - p$ 可能性被dropout掉，即 $b_l=0$ 。

当然，在实际操作的时候，作者是将“线性衰减规律”应用到了每一层的生存概率，因为他们觉得较早的层会提取低级特征，而这些基础特征对后面的层很重要，所以这些层不应该频繁的丢弃主分支。而随着后面层提取的特征越来越抽象，冗余度可能更高，所以越到后面，这个丢弃主分支的概率就增加，具体计算公式如下：
$p_{\ell}=1-\frac{\ell}{L}\left(1-p_{L}\right)$
这里的 $p_l$ 表示 $l$ 层训练中主分支的保留概率， $L$ 是block块的总数量， $p_L$ 是我们给出的dropout_rate。 $l$ 是表示 $l$ 层的残差块。

实验表明，同样是训练一个110层的ResNet，以任意深度进行训练的性能，比以固定深度进行训练的性能要好。这就意味着ResNet中的一些层（路径）可能是冗余的。

所以这种训练方式的优点：

成果解决深度网络训练时间难题
大大减少训练时间，并显著改善网络的精度
可以使得网络更深

当然，这里的原理不是很难，下面主要是从代码层面看看具体是怎么实现的。

这里拿EfficientNet网络里面的代码进行说明，其他的也都类似：

# kernel_size, in_channel, out_channel, exp_ratio, strides, use_SE, drop_connect_rate, repeats
default_cnf = [[3, 32, 16, 1, 1, True, drop_connect_rate, 1],[3, 16, 24, 6, 2, True, drop_connect_rate, 2],[5, 24, 40, 6, 2, True, drop_connect_rate, 2],[3, 40, 80, 6, 2, True, drop_connect_rate, 3],[5, 80, 112, 6, 1, True, drop_connect_rate, 3],[5, 112, 192, 6, 2, True, drop_connect_rate, 4],[3, 192, 320, 6, 1, True, drop_connect_rate, 1]]

这里给出每个stage的配置，这个具体不用管，这个看EfficientNet的网络结构就知道。
在这里插入图片描述
这里是修改配置的代码，也就是会遍历上面的每个stage，然后根据重复次数建立残差块，这里的残差块是倒残差模块，开头的那个图里面的结构。主要是框出来的这句话，就是“线性衰减规律”的那个公式，这里的cnf[-1]表示的当前残差块的dropout_rate，而args[-2]是我们指定的dropout_rate， $b$ 表示当前 $l$ 层， num_blocks就是总的blocks数，和上面公式一一对应。

这里就会发现，搭建网络的时候，每个残差块都会指定一个dropout_rate，那么在每个残差块里面，我们搭建的dropout层如下，这里直接拿EfficientNetV1来看，重点关注self.dropout即可，上面的那些是主分支上的扩张卷积，dw卷积以及降维卷积，不是这篇文章的重点：

class InvertedResidualEfficientNetV1(nn.Module):def __init__(self,cnf: InvertedResidualConfigEfficientNet,norm_layer: Callable[..., nn.Module]):super(InvertedResidualEfficientNetV1, self).__init__()self.use_res_connect = (cnf.stride == 1 and cnf.input_c == cnf.out_c)layers = OrderedDict()activation_layer = nn.SiLU  # alias Swish# expandif cnf.expanded_c != cnf.input_c:layers.update({"expand_conv": ConvBNActivation(cnf.input_c,cnf.expanded_c,kernel_size=1,norm_layer=norm_layer,activation_layer=activation_layer)})# depthwiselayers.update({"dwconv": ConvBNActivation(cnf.expanded_c,cnf.expanded_c,kernel_size=cnf.kernel,stride=cnf.stride,groups=cnf.expanded_c,norm_layer=norm_layer,activation_layer=activation_layer)})if cnf.use_se:layers.update({"se": SqueezeExcitationV2(cnf.input_c,cnf.expanded_c)})# projectlayers.update({"project_conv": ConvBNActivation(cnf.expanded_c,cnf.out_c,kernel_size=1,norm_layer=norm_layer,activation_layer=nn.Identity)})self.block = nn.Sequential(layers)self.out_channels = cnf.out_cself.is_strided = cnf.stride > 1# 只有在使用shortcut连接时才使用dropout层if self.use_res_connect and cnf.drop_rate > 0:self.dropout = DropPath(cnf.drop_rate)else:self.dropout = nn.Identity()def forward(self, x: Tensor) -> Tensor:result = self.block(x)result = self.dropout(result)if self.use_res_connect:result += x

这里的代码细节不用多说，其实就是开头的那个残差网络结构，我们主要看看啥时候使用Dropout，只有使用跳远连接，以及当前的dropout_rate大于0的时候，我们的Dropout层会走一个DropPath，否则不是残差结构，或者没有dropout_rate，那么我们就恒等过去，所以DropoutPath只用于残差结构。

那么DropPath是怎么实现呢？

class DropPath(nn.Module):def __init__(self, drop_prob=None):super(DropPath, self).__init__()self.drop_prob = drop_probdef forward(self, x):return drop_path(x, self.drop_prob, self.training)

这里是建了一个DropPath层，这里的核心实现是drop_path函数，在这里面，实现的就是根据给定的dropout_rate概率随机失活主分支。所以重点看看这个的实现逻辑：

def drop_path(x, drop_prob: float = 0, training: bool = False):if drop_prob == 0. or not training:return xkeep_prob = 1 - drop_prob# ndim是维度个数  x.shape[0] 是样本个数， shape: (x.shape[0], 1, 1, 1)  维度可以用+拼接shape = (x.shape[0], ) + (1, ) * (x.ndim - 1)# 为每个样本生成一个随机数 torch.rand[0, 1), keep_prob (0, 1]， 两者之和是[0, 2)  形状是(x.shape[0], 1, 1, 1)random_tensor = keep_prob + torch.rand(shape, dtype=x.dtype, device=x.device)  # torch.rand 均匀分布抽取的随机数([0,1))# 下取整，即random_tensor非0即1  形状(x.shape[0], 1, 1, 1)random_tensor.floor_()    # 下取整# 这里随机失活主分支， 除以keep_prob是为了保持训练和测试的尺度一致，普通dropout思路output = x.div(keep_prob) * random_tensorreturn output

这里为了弄明白，我每一行代码就加了注释。其实逻辑很简单，对于我们一个batch里面的样本，比如 $n$ 个，那么输入x的形状就是 $n, channel_{size}, h, w)$ ，我们首先会每个样本，都会生成一个[0,2)之间的随机数，然后下取整，就得到了非0即1的random_tensor，这个其实就是我们的 $b_l$ ，每个样本对应一个，所以每个样本训练的时候，都会看看是否激活主分支。然后具体是否激活，就是最后一行代码做的事情，这里除以keep_prob是为了保证训练集和测试集的尺度范围一致，和普通的dropout一样。