TOPSIS法简称优劣解距离法,是一种常用的综合评价法,其能充分利用原始数据的信息,其结果能精确地反映各评价方案之间的差距。
层次分析法的一些局限性
(1)评价的决策层不能太多,太多的话n会很大,判断矩阵和一致矩阵差异可能会很大
(2)如果决策层指标的数据是已知的,那么我们如何利用这些数据来使得评价的更加准确呢?
例如:
| 学生 | 加权成绩 | 工时数 | 课外竞赛得分 |
| A | 89.7 | 32 | 5 |
| B | 86.5 | 20 | 4 |
| C | 87 | 14 | 6 |
| D | 88 | 38 | 9 |
| ... | ... | ... | ... |
如何利用已知的数据来推举出优秀学生?(显然不能使用层次分析法,这时应使用TOPSIS法)
TOPSIS法三点解释
(1)比较的对象一般要远大于两个。(例如比较一个班级的成绩)
(2)比较的指标也往往不只是一个方面的,例如成绩、工时数、课外竞赛得分等。
(3)有很多指标不存在理论上的最大值和最小值,例如衡量经济增长水平的指标:GDP增速。
构造计算评分的公式:
![]()
成绩是越高(大)越好,这样的指标称为极大型指标(效益型指标)。
与他人争吵的次数越少(越小)越好,这样的指标称为极小型指标(成本型指标)。
这种时候应统一指标类型:将所有的指标转化为极大型称为指标正向化(最常用)
极小型指标转换为极大型指标的公式: max-x
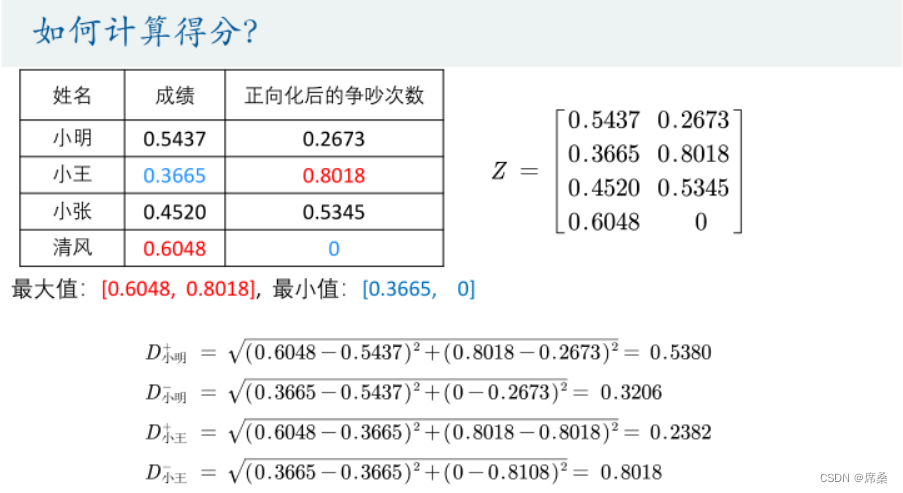
姓名 成绩(分) 与他人争吵的次数(次) 正向化后的争吵次数
小明 89 2 1
小王 60 0 3
小张 74 1 2
清风 99 3 0
指标类型 极大型 极小型 极大型
为了消去不同指标量纲的影响,需要对已经正向化的矩阵进行标准化处理。

标准化不会影响相对大小。
如何计算得分?
只有一个指标的时候:
构造计算评分的公式:
![]()
变形:

可看作:
𝒙与最小值的距离 / 𝒙与最大值的距离 + 𝒙与最小值的距离

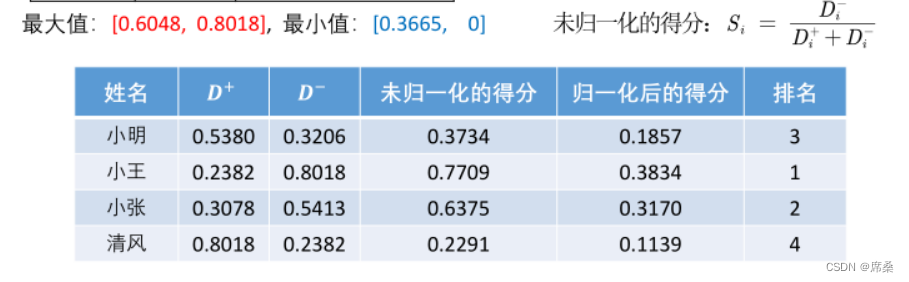
归一化得出得分后进行排序。
基本过程
1.将原始数据矩阵统一指标类型(一般正向化处理)得到正向化的矩阵,
2.对正向化的矩阵进行标准化处理以消除各指标量纲的影响,并找到有限方案中的最优方案和最劣方案,
3.分别计算各评价对象与最优方案和最劣方案间的距离,获得各评价对象与最优方案的相对接近程度,以此作为评价优劣的依据。
该方法对数据分布及样本含量没有严格限制,数据计算简单易行。
第一步:将原始矩阵正向化
| 指标名称 | 指标特点 | 例子 |
| 极大型(效益型)指标 | 越大(多)越好 | 成绩、GDP增速、企业利润 |
| 极小型(成本型)指标 | 越小(少)越好 | 费用、坏品率、污染程度 |
| 中间型指标 | 越接近某个值越好 | 水质量评估时的PH值 |
| 区间型指标 | 落在某个区间最好 | 体温、水中植物性营养物量 |
所谓的将原始矩阵正向化,就是要将所有的指标类型统一转化为极大型指标。(转换的函数形式可以不唯一 )
极小型指标 极大型指标:
极大型指标:
极小型指标转换为极大型指标的公式:max-x(如果所有的元素均为正数,那么也可以使用 )
中间型指标 极大型指标:
极大型指标:
中间型指标:指标值既不要太大也不要太小,取某特定值最好(如水质量评估 PH 值)

注意:正向化的公式不唯一,大家也可以结合自己的数据进行适当的修改。
区间型指标 极大型指标
极大型指标
区间型指标:指标值落在某个区间内最好,例如人的体温在36°~37°这个区间比较好。

第二步:正向化矩阵标准化
标准化的目的是消除不同指标量纲的影响。

第三步:计算得分并归一化

模型拓展:
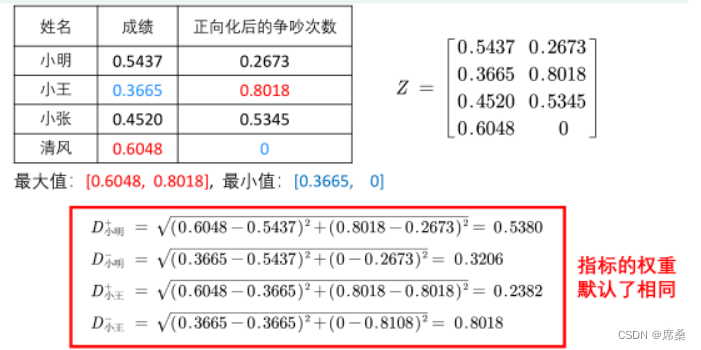
问题:计算得分时指标的权重默认为相同的
改进方法:计算得分时乘以权重

带权重的TOPSIS法:

缺点:层次分析法的主观性太强了,更推荐大家使用熵权法来进行客观赋值。
代码优化:
请你改编代码,使用户能选择是否加入指标的权重计算。
提示:用if函数判断用户的输入
感谢观看!