目录
问题分析
模型建立
Logistic模型
Leslie模型
模型求解
问题一
问题二
问题三
问题分析
问题
基本假设
(1)不考虑移民对人口总数的影响
(2)超过90岁按照90岁计算
(3)在较短时间内,平均年龄变化较小,可认为不变
(4)社会稳定,不会发生重大灾害和战争,出生率和死亡率基本不变
模型建立
Logistic模型

Leslie模型

模型求解
inline
f = inline(expr)按照expr中包含的 MATLAB® 表达式构造一个内联函数对象。内联函数的输入参数是通过在expr中搜索孤立的小写字母字符(i或j除外)自动确定的,该小写字母字符不属于通过多个字母字符构成的字词的一部分。如果不存在此类字符,则使用x。如果该字符不是唯一的,则使用最接近x的字符。如果找到两个字符,则选择在字母表中靠后的字符。
f = inline(expr,arg1,arg2,…,argN)构造一个由arg1,arg2,…,argN指定输入参数的内联函数。可以使用多字符符号名称。
f = inline(expr,N)(其中N是标量)构造一个其输入参数为x和P1,P2,…,PN的内联函数
sqr = @(x) x.^2
(比起inline,更加推荐使用匿名函数)
变量
sqr是一个函数句柄。@运算符创建句柄,@运算符后面的圆括号()包括函数的输入参数。该匿名函数接受单个输入x,并显式返回单个输出,即大小与包含平方值的x相同的数组。通过将特定值 (
5) 传递到函数句柄来计算该值的平方,与您将输入参数传递到标准函数一样。
nlinfit 非线性回归
beta = nlinfit(X,Y,modelfun,beta0)使用modelfun指定的模型,返回一个向量,其中包含Y中的响应对X中的预测变量的非线性回归的估计系数。它使用迭代最小二乘估计来估计系数,初始值由beta0指定。
beta = nlinfit(X,Y,modelfun,beta0,options)使用结构体options中的算法控制参数来拟合非线性回归。您可以返回上述语法中的任何输出参数。
beta = nlinfit(___,Name,Value)使用由一个或多个名称-值对组参数指定的附加选项。例如,您可以指定观测值权重或非常量误差模型。您可以使用上述语法中的任何输入参数。
[beta,R,J,CovB,MSE,ErrorModelInfo] = nlinfit(___)还返回残差R、modelfun的 Jacobian 矩阵J、估计系数的估计方差-协方差矩阵CovB、误差项的方差估计MSE以及包含误差模型细节的结构体ErrorModelInfo。
问题一
Logistic模型根据经济发展水平、政策情况,分为三个时间段(三种情况)对问题进行求解。
①将1954年看成初始年t=0;1955年为t=1;2005年为t=51,作为终止时刻。
clear all
clc
t=0:51; %令1954年为初始年
x=[60.2 61.5 62.8 64.6 66 67.2 66.2 65.9 67.3 69.1 70.4 72.5 74.5 76.3 78.5 80.7 83 85.2 87.1 89.2 90.9 92.4 93.7 95 96.259 97.5 98.705 100.1 101.654 103.008 104.357 105.851 107.5 109.3 111.026 112.704 114.333 115.823 117.171 118.517 119.85 121.121 122.389 123.626 124.761 125.786 126.743 127.627 128.453 129.227 129.988 130.756]; syms c d
c/(1+(c/60.2-1)*exp(-5*d))==67.2
c/(1+(c/60.2-1)*exp(-20*d))==90.9
%求初始参数
solve(c,d)b0=[ 241.9598, 0.02985]; %初始参数值
fun=inline('b(1)./(1+(b(1)/60.2-1).*exp(-b(2).*t))','b','t');
[b1,r1,j1]=nlinfit(t,x,fun,b0)
y=180.9871./(1+( 180.9871/60.2-1).*exp( -0.0336.*t)); %非线性拟合的方程
figure(1)
plot(t,x,'*',t,y,'-or') %对原始数据与曲线拟合后的值作图
title('原始数据与曲线拟合后曲线')
xlabel('时间')
ylabel('人口数量(单位:千万)')
R1=r1.^2;
R2=(x-mean(x)).^2;
R=1-R1/R2'; %可决系数
W=sum(abs(r1)) %残差绝对值之和
% t=56;
% y56=180.9871./(1+( 180.9871/60.2-1).*exp( -0.0336.*t)) %非线性拟合的方程
% t=66;
% y66=180.9871./(1+( 180.9871/60.2-1).*exp( -0.0336.*t)) %非线性拟合的方程
% t=79;
% y79=180.9871./(1+( 180.9871/60.2-1).*exp( -0.0336.*t)) %非线性拟合的方程
% %1954年到2005年的总人口数进行拟合产生的残差散点图
% figure(2)
% t=1954:2005;
% plot(t,r1,'.-')
②将1963年看为t=0;2005年为终止年,t=42。
clear all
clc
t=46:3:94
y= 180.9871./(1+( 180.9871/60.2-1).*exp( -0.0336.*t))%对总人口进行预测
t=0:42; %令1963年为初始年
x=[69.1 70.4 72.5 74.5 76.3 78.5 80.7 83 85.2 87.1 89.2 90.9 92.4 93.7 95 96.259 97.5 98.705 100.1 101.654 103.008 104.357 105.851 107.5 109.3 111.026 112.704 114.333 115.823 117.171 118.517 119.85 121.121 122.389 123.626 124.761 125.786 126.743 127.627 128.453 129.227 129.988 130.756]; syms c d
c/(1+(c/69.1-1)*exp(-5*d))==78.5
c/(1+(c/69.1-1)*exp(-20*d))==103.008 %求初始参数
solve(c,d)b0=[ 134.368,0.056610]; %初始参数值
fun=inline('b(1)./(1+(b(1)/69.1-1).*exp(-b(2).*t))','b','t');
[b1,r1,j1]=nlinfit(t,x,fun,b0)
y=151.4513./(1+(151.4513/69.1-1).*exp( -0.0484.*t)); %非线性拟合的方程
figure(1)
plot(t,x,'*',t,y,'-or') %对原始数据与曲线拟合后的值作图
title('原始数据与曲线拟合后曲线')
xlabel('时间')
ylabel('人口数量(单位:千万)')
R1=r1.^2;
R2=(x-mean(x)).^2;
R=1-R1/R2'; %可决系数
W=sum(abs(r1)) %残差绝对值之和
% t=47;
% y47=151.4513./(1+(151.4513/69.1-1).*exp( -0.0484.*t)) %非线性拟合的方程
% t=57;
% y57=151.4513./(1+(151.4513/69.1-1).*exp( -0.0484.*t)) %非线性拟合的方程
% t=70;
% y70=151.4513./(1+(151.4513/69.1-1).*exp( -0.0484.*t)) %非线性拟合的方程
% %1963年到2005年的总人口数进行拟合产生的残差散点图
% figure(2)
% t=1963:2005;
% plot(t,r1,'.-')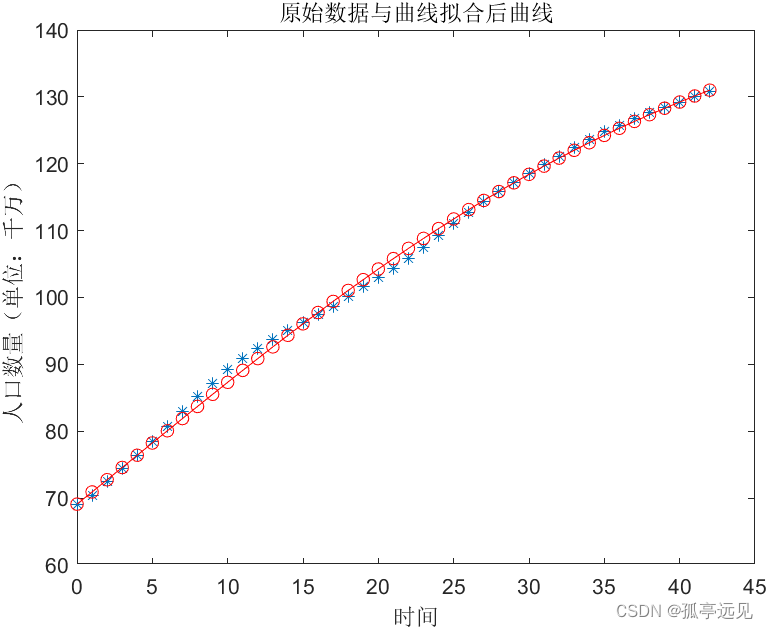
③将1980年看为起始年,2005年视为终止年
clear all
clc
t=37:3:85
y=151.4513./(1+(151.4513/69.1-1).*exp( -0.0484.*t))%对总人口进行预测
t=0:25; %令1980年为初始年
x=[98.705 100.1 101.654 103.008 104.357 105.851 107.5 109.3 111.026 112.704 114.333 115.823 117.171 118.517 119.85 121.121 122.389 123.626 124.761 125.786 126.743 127.627 128.453 129.227 129.988 130.756]; syms c d
c/(1+(c/98.705-1)*exp(-5*d))==105.851
c/(1+(c/98.705-1)*exp(-8*d))==111.026
solve(c,d)%求初始参数
b0=[ 109.8216, - 0.19157]; %初始参数值
fun=inline('b(1)./(1+(b(1)/98.705-1).*exp(-b(2).*t))','b','t');
[b1,r1,j1]=nlinfit(t,x,fun,b0)
y= 153.5351./(1+(153.5351/98.705-1).*exp( -0.0477.*t)); %非线性拟合的方程
figure(1)
plot(t,x,'*',t,y,'-or') %对原始数据与曲线拟合后的值作图
title('原始数据与曲线拟合后曲线')
xlabel('时间')
ylabel('人口数量(单位:千万)')
R1=r1.^2;
R2=(x-mean(x)).^2;
R=1-R1/R2'; %可决系数W=sum(abs(r1)) %残差绝对值之和
% t=20:3:53;
% y= 153.5351./(1+(153.5351/98.705-1).*exp( -0.0477.*t))%对总人口进行预测
% %1954年到2005年的总人口数进行拟合产生的残差散点图
% figure(2)
% t=1980:2005;
% plot(t,r1,'.-')
% grid on
问题二
采用考虑种群结构的Leslie离散模型。
clear all
clc
%计算2001到2051年的人口总数程序
p=0.464429182; %女性占总人口的比例
N=[0.680891272 0.58459172 0.584558207 0.692220217 0.72411021 0.775536041 0.847368918 0.834418703 0.917922042 0.951466819 1.070015717 1.249256063 1.199263988 1.202198525 1.274218917 1.111050839 0.992314425 0.893797544 0.874657347 0.984356877 0.859576778 0.85215346 0.90864418 0.897944807 0.880539323 1.019086724 1.04218667 1.114823731 1.192867199 1.203566572 1.272973995 1.328513576 1.254992403 1.333819445 1.103186123 1.22470307 1.220643442 1.236736319 1.390726415 0.980765111 0.646684069 0.785660623 0.701627592 0.910420112 0.960157646 0.914258713 0.953980568 0.927429956 0.851007759 0.825482359 0.807942823 0.736552002 0.69043204 0.60580295 0.615510624 0.554785663 0.50370135 0.480051762 0.468722817 0.455364059 0.484386541 0.447344681 0.420164498 0.44238033 0.426529091 0.428183875 0.39132953 0.380409129 0.385339967 0.327924574 0.334697711 0.307330012 0.262864834 0.270663183 0.235872165 0.208725495 0.212001549 0.178456772 0.164260316 0.149842833 0.138734916 0.109899949 0.097358277 0.0765762 0.0638135 0.055794123 0.049396016 0.0382881 0.033544777 0.023870616 0.070211606];
N0=N'/10; %第0年(2001年)的女性各个年龄段的人口数(千万)
N00=N0/10 %把单位化成亿(人)
A=eye(90);
b=[0.974906966 0.999321231 0.99772433 0.999247616 0.999567418 0.999180663 0.999887948 0.999387596 0.999618586 0.999985672 0.999389434 0.999724354 0.999801796 0.999627626 0.999704795 0.999639686 0.999728462 0.999974533 0.999173327 0.998954118 0.999441067 0.999357392 0.999290675 0.998999176 0.999881604 0.998896347 0.998355939 0.999135339 0.999074527 0.998872652 0.999180794 0.998918159 0.999046112 0.999042354 0.999396027 0.998624972 0.998252716 0.999597855 0.998710945 0.999003274 0.999443444 0.999141415 0.998772101 0.998940505 0.997905005 0.998374562 0.997783774 0.997596666 0.997344906 0.996954499 0.996669784 0.996030759 0.995006639 0.996157488 0.994647744 0.995779435 0.995652313 0.99577713 0.992477806 0.994969564 0.988130537 0.989284868 0.988703961 0.988302563 0.98420824 0.984495416 0.985298735 0.980062089 0.978928307 0.977358446 0.971126989 0.969303899 0.969979818 0.96405059 0.961740312 0.96729706 0.948302346 0.946571559 0.949641387 0.935949391 0.912489482 0.9261805 0.923757863 0.928757906 0.918230333 0.887761389 0.885306858 0.875178086 0.882495752 0.824428701];
for i=1:90A(i,:)=A(i,:)*b(1,i);
end
A;
c=[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 4.478E-05 0.000322169 0.000358246 0.001004604 0.004683367 0.011011165 0.033616492 0.057875394 0.074871727 0.069182006 0.076039141 0.06724895 0.052429406 0.043732464 0.034350502 0.024632733 0.023252532 0.018343847 0.014701275 0.011039961 0.007117557 0.005094843 0.00359291 0.002514858 0.002484781 0.001764709 0.001471644 0.000676953 0.000265476 0.000401474 0.000408779 0.000110447 0.000192401 0.000389421 0.000224069 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]; %由2001年原始数据得到的生育率
c1=1.295274487*c; %修正后的生育率
M=sum(c1'); %总合生育率
d=zeros(91,1);
B=[c1;A];
L=[B,d]; %构造的lestie矩阵
for i=0:1:50
X=L^i*N0; %第i年后女性各个年龄段的人口数(千万)
Z=X./p; %第i年在各个年龄段的人口总数预测
K(i+1,1)=sum(Z);
S1=sum(Z([1:15],:)); %第i年0-14岁的总人数
D(1,i+1)=S1;
S2=sum(Z([16:65],:)); %第i年15-64岁的总人数
S3=sum(Z([61:91],:)); %第i年60-90岁人数
G(1,i+1)=S3;
E(1,i+1)=S2;
S4=sum(Z([66:91],:)); %第i年65-90岁人数
F(1,i+1)=S4;
end
K %2001-2051的人口总数
D %年龄在0-14岁总人数(包括男女)
E %年龄在15-64岁总人数(包括男女)
F %年龄在65岁及65岁以上总人数(包括男女)
G %年龄在60岁及60岁以上总人数(包括男女)
%我国全国总人口与劳动年龄人口
x=2001:2051;
y1=K;
y2=E';
figure(1)
plot(x,y1,'*',x,y2,'-or')
title('我国全国总人口与劳动年龄人口变化趋势');
xlabel('时间');
ylabel('人口变化趋势')
%我国60岁以上与65岁以上的老龄人口数
x=2001:2051;
y1=G';
y2=F';
figure(2)
plot(x,y1,'*',x,y2,'-or')
title('我国60岁以上与65岁以上的老龄人口数');
xlabel('时间');
ylabel('老龄人口数')
%我国老龄人口占总人口预测比例
x=2001:2051;
y1=G'/K;
y2=F'/K;
figure(3)
plot(x,y1(:,23),'*',x,y2(:,23),'-or')
title('我国老龄人口占总人口预测比例');
xlabel('时间');
ylabel('老龄人口比重')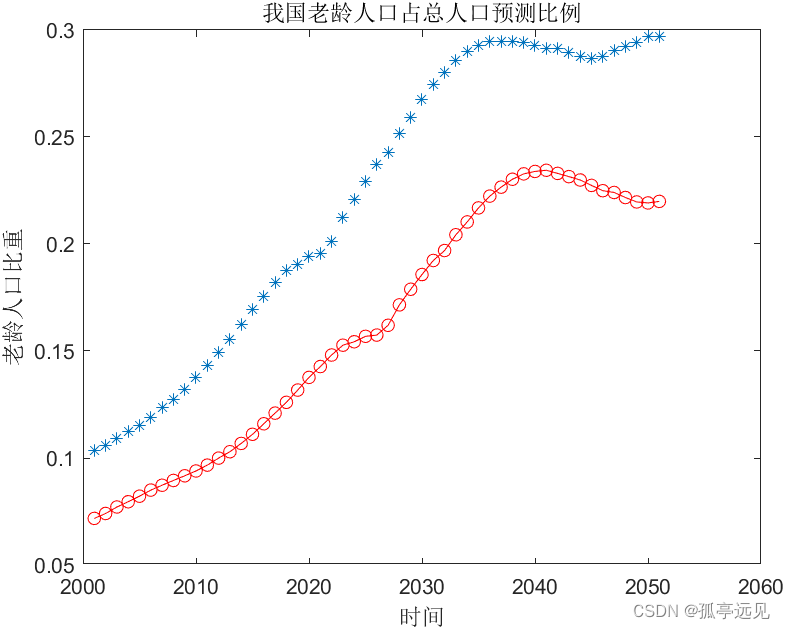
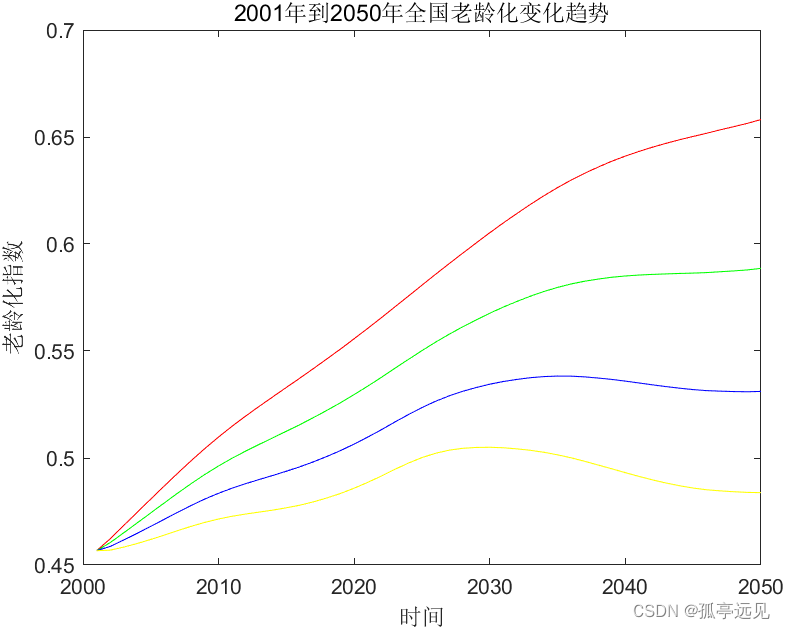
问题三
在不同的总生育率k下预测全国老龄化变化趋势。
function W=compare(x)
p=0.464429182; %女性占总人口的比例
N=[0.680891272 0.58459172 0.584558207 0.692220217 0.72411021 0.775536041 0.847368918 0.834418703 0.917922042 0.951466819 1.070015717 1.249256063 1.199263988 1.202198525 1.274218917 1.111050839 0.992314425 0.893797544 0.874657347 0.984356877 0.859576778 0.85215346 0.90864418 0.897944807 0.880539323 1.019086724 1.04218667 1.114823731 1.192867199 1.203566572 1.272973995 1.328513576 1.254992403 1.333819445 1.103186123 1.22470307 1.220643442 1.236736319 1.390726415 0.980765111 0.646684069 0.785660623 0.701627592 0.910420112 0.960157646 0.914258713 0.953980568 0.927429956 0.851007759 0.825482359 0.807942823 0.736552002 0.69043204 0.60580295 0.615510624 0.554785663 0.50370135 0.480051762 0.468722817 0.455364059 0.484386541 0.447344681 0.420164498 0.44238033 0.426529091 0.428183875 0.39132953 0.380409129 0.385339967 0.327924574 0.334697711 0.307330012 0.262864834 0.270663183 0.235872165 0.208725495 0.212001549 0.178456772 0.164260316 0.149842833 0.138734916 0.109899949 0.097358277 0.0765762 0.0638135 0.055794123 0.049396016 0.0382881 0.033544777 0.023870616 0.070211606];
N0=N';
A=eye(90);
b=[0.974906966 0.999321231 0.99772433 0.999247616 0.999567418 0.999180663 0.999887948 0.999387596 0.999618586 0.999985672 0.999389434 0.999724354 0.999801796 0.999627626 0.999704795 0.999639686 0.999728462 0.999974533 0.999173327 0.998954118 0.999441067 0.999357392 0.999290675 0.998999176 0.999881604 0.998896347 0.998355939 0.999135339 0.999074527 0.998872652 0.999180794 0.998918159 0.999046112 0.999042354 0.999396027 0.998624972 0.998252716 0.999597855 0.998710945 0.999003274 0.999443444 0.999141415 0.998772101 0.998940505 0.997905005 0.998374562 0.997783774 0.997596666 0.997344906 0.996954499 0.996669784 0.996030759 0.995006639 0.996157488 0.994647744 0.995779435 0.995652313 0.99577713 0.992477806 0.994969564 0.988130537 0.989284868 0.988703961 0.988302563 0.98420824 0.984495416 0.985298735 0.980062089 0.978928307 0.977358446 0.971126989 0.969303899 0.969979818 0.96405059 0.961740312 0.96729706 0.948302346 0.946571559 0.949641387 0.935949391 0.912489482 0.9261805 0.923757863 0.928757906 0.918230333 0.887761389 0.885306858 0.875178086 0.882495752 0.824428701];
b1=[0.974906966 0.999321231 0.99772433 0.999247616 0.999567418 0.999180663 0.999887948 0.999387596 0.999618586 0.999985672 0.999389434 0.999724354 0.999801796 0.999627626 0.999704795 0.999639686 0.999728462 0.999974533 0.999173327 0.998954118 0.999441067 0.999357392 0.999290675 0.998999176 0.999881604 0.998896347 0.998355939 0.999135339 0.999074527 0.998872652 0.999180794 0.998918159 0.999046112 0.999042354 0.999396027 0.998624972 0.998252716 0.999597855 0.998710945 0.999003274 0.999443444 0.999141415 0.998772101 0.998940505 0.997905005 0.998374562 0.997783774 0.997596666 0.997344906 0.996954499 0.996669784 0.996030759 0.995006639 0.996157488 0.994647744 0.995779435 0.995652313 0.99577713 0.992477806 0.994969564 0.988130537 0.989284868 0.988703961 0.988302563 0.98420824 0.984495416 0.985298735 0.980062089 0.978928307 0.977358446 0.971126989 0.969303899 0.969979818 0.96405059 0.961740312 0.96729706 0.948302346 0.946571559 0.949641387 0.935949391 0.912489482 0.9261805 0.923757863 0.928757906 0.918230333 0.887761389 0.885306858 0.875178086 0.882495752 0.824428701 0.7717624];
for i=1:90A(i,:)=A(i,:)*b(1,i);
end
A;
c1=[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 4.478E-05 0.000322169 0.000358246 0.001004604 0.004683367 0.011011165 0.033616492 0.057875394 0.074871727 0.069182006 0.076039141 0.06724895 0.052429406 0.043732464 0.034350502 0.024632733 0.023252532 0.018343847 0.014701275 0.011039961 0.007117557 0.005094843 0.00359291 0.002514858 0.002484781 0.001764709 0.001471644 0.000676953 0.000265476 0.000401474 0.000408779 0.000110447 0.000192401 0.000389421 0.000224069 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]; %由2001年原始数据得到的生育率
t=sum(c1);
c=((x*p-t)/t+1)*c1 %修正后的生育率
M=sum(c'); %总合生育率
d=zeros(91,1);
B=[c;A];
L=[B,d]; %构造的lestie矩阵
[V,d]=eig(L); %求特征根与特征向量
p=d(42,42); %特征根
Q=-V(:,42); %对应的正特征向量
for i=0:49D=L^i*N0; %第i年女性人口分布E(i+1,1)=sum(D)/p %第i年总人口(2001为第0年)for j=0:90 %大于90岁的按90岁算F(j+1,1)=j*D(j+1,1)/p;T(j+1,1)=exp(-b1(1,j+1)); endY(i+1)=sum(F)/E(i+1,1); %平均年龄
end
Y %输出01-50年平均年龄矩阵
T=0;
s=0;for i=0:90 %大于90岁的按90岁算T=T+exp(b1(1,j+1)-1); %求平均寿命,不随年份而变化endTW=Y/T; %社会老龄化指数
% x=2001:2050;
% W1=compare(1.6);
% W2=compare(1.8);
% W3=compare(2.0);
% W4=compare(2.2);
% plot(x,W1,'-r')
% hold on
% plot(x,W2,'-G')
% plot(x,W3,'-B')
% plot(x,W4,'-Y')
% title('2001年到2050年全国老龄化变化趋势')
% xlabel('时间')
% ylabel('全国总人口')对函数进行调用:
x=2001:2050;
W1=compare(1.5);
W2=compare(2.0);
W3=compare(2.5);
W4=compare(3.0);
plot(x,W1,'-r');
hold on
plot(x,W2,'-G');
plot(x,W3,'-B');
plot(x,W4,'-Y');
title('2001年到2050年全国老龄化变化趋势');
xlabel('时间');
ylabel('老龄化指数');