一、理论基础

在进行数据采集的过程中，需要根据实际情况选择合适的采集设备，现有的采集设备一般都是由多个传感器模块、显示模块、电源模块以及通信模块构成。在本课题中，我们选择了BWT61CL无线蓝牙版带电池陀螺仪姿态传感器作为本文的数据采集设备。该设备的主要参数指标如下表所示：

表1陀螺仪姿态传感器参数指标

	参数名称	参数值
1	电压	3.3V~5V
2	电流	<10mA
3	尺寸	51.3mm36mm15mm
4	测量精度	0.05
5	量程	加速度16g，角速度2000度/s，角度180度
6	分辨率	加速度6.1e-5g，角速度7.6e-3度/s
7	测量维度	三维
8	输出频率	100Hz

BWT61CL姿态传感器其主要构架包括了传感器模块、信号处理单元、信号收发接口等模块，其具有低功耗、低成本、轻便等优势[19]。该设备广泛应用于手机，GPS导航、计步器以及智能儿童手表等电子产品中，下面对该IMU设备的各个模块进行介绍。

3.2.1加速度计

加速度计是BWT61CL姿态传感器的一个重要组成部分，其属于惯性传感器的一种，通过加速度计可以采集人体的加速度信息，包括x轴加速度，y轴加速度以及z轴加速度。当人体在行走或者奔跑过程中，其加速度将表现为周期性的波动，那么通过加速度计则可以实时监测这种周期性变化，并根据这种周期特征来计算人体的步态和步伐数量。当人体处于静止状态或者匀速状态，此时加速度计只有垂直方向有数据，且近似为重力加速度。

3.2.2陀螺仪

陀螺仪同样是BWT61CL姿态传感器的一个重要组成部分，通过陀螺仪可以实时监测出人体在行走过程中的角速度。BWT61CL中的陀螺仪，其转轴方向将不随着支架的转动而变化，当设备收到外部角度变化的时候，其上下金属之间的电容会发生变化，根据电压值的改变大小来判断角度的变化大小。

3.3基于IMU设备的人体步态数据的采集

数据采集环节是人体步行识别和步伐统计研究的第一环节，在本课题中，我们主要通过BWT61CL姿态传感器进行采集行人的xyz三个方向的加速度，xyz三个方向的角速度以及xyz三个方向的角度（如图3.1所示），为课题的研究提供最原始的分析数据。

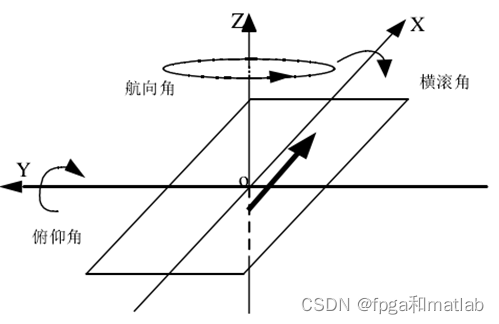
图1数据采集示意图

通过采集得到的数据主要包括人体沿着x轴、y轴、z轴的加速度，即ax，ay，az；沿着x轴、y轴、z轴的姿态角，即横滚角anglex，俯仰角angley，偏航角anglez，沿着x轴、y轴、z轴的角速度，即wx，wy，wz；一共九组特征数据。由图3.1可知，横滚角以x轴作为旋转轴，俯仰角以y轴作为旋转轴，航偏角以z轴为旋转轴。通过IMU设备对数据进行实时的采集，可以记录行人不同的行走状态。最终采集的数据结构如下所示：

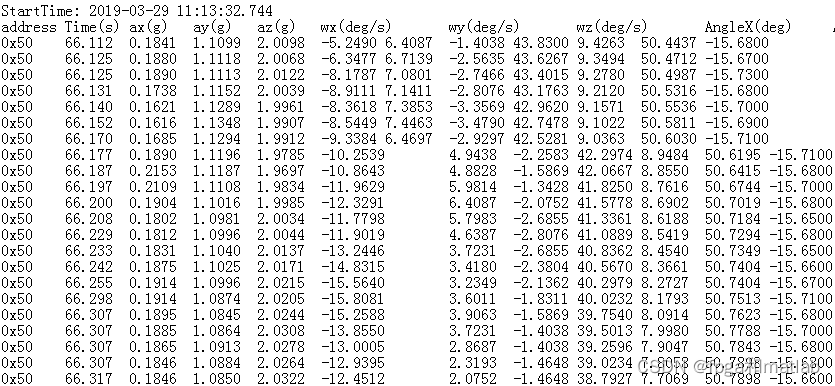
图2数据样本图

二、MATLAB仿真程序

clc;
clear;
close all;
warning off;sel = 2;    load R1.mat[locsy1,indxy1]=func_peak(ay1);
[locsz1,indxz1]=func_peak(az1);[locsy2,indxy2]=func_peak(ay2);
[locsz2,indxz2]=func_peak(az2);[locsy3,indxy3]=func_peak(ay3);
[locsz3,indxz3]=func_peak(az3);if sel == 1figure;
subplot(211);
plot(Timesa,ay1,'b');
hold on
plot(Timesa(locsy1),ay1(locsy1),'ro'); 
hold on
plot(Timesa(indxy1),ay1(indxy1),'k*'); 
hold on
stem(Timesa(locsy1),ay1(locsy1),'ro')
xlabel('time');
ylabel('ay');
subplot(212);
plot(Timesa,az1,'b');;
hold on
plot(Timesa(locsz1),az1(locsz1),'ro');
hold on
plot(Timesa(indxz1),az1(indxz1),'k*');
hold on
stem(Timesa(locsz1),az1(locsz1),'ro')
xlabel('time');
ylabel('az');Tay1  =[Timesa(locsy1)]';
Tby1  =[Timesa(indxy1)]';
Ay1  =[ay1(locsy1)]'; Taz1  =[Timesa(locsz1)]';
Tbz1  =[Timesa(indxz1)]';
Az1  =[az1(locsz1)]'; ptime1 = [67.574,68.031,68.602,69.235,69.775,70.352,70.922,71.636,72.201,72.66,73.212];
ptime2 = [67.407,68.12,68.762,69.347,69.881,70.448,70.998,71.567,72.20,72.755,73.307];for i = 1:length(ptime1)-1diff1(1,i)=ptime1(i+1)-ptime1(i);diff2(1,i)=ptime2(i+1)-ptime2(i);
end
2*mean(diff1)
2*mean(diff2)
figure;
plot(ptime1-ptime2);p1=[66.2,66.402,66.519,66.746,66.951,67.05,67.198,67.343,67.499,67.615,67.913,68.201,68.531,68.868,69.155,69.393,69.698,69.991,70.235,70.559,70.802,71.145,71.381,71.687,71.972,72.288,72.53,72.844,73.104,73.431,73.707,73.858];
p2=[66.936,67.170,67.360,67.499,68.021,68.333,68.531,	68.554,68.629,68.951,69.222,69.56,69.798,70.021,70.378,70.596,70.611,70.661,70.667,70.671,70.979,71.197,71.553,71.794,72.1,72.321,72.678,72.911,73.245,73.423,73.493,73.847,73.994];for i = 1:length(p1)-1diff1(1,i)=p1(i+1)-p1(i);diff2(1,i)=p2(i+1)-p2(i);
end
5*mean(diff1)
5*mean(diff2)ay=mean(sqrt(ax1(locsz1).^2 + ay1(locsz1).^2 + az1(locsz1).^2))endif sel == 2
figure;
subplot(211);
plot(Times2,ay2,'b');
hold on
plot(Times2(locsy2),ay2(locsy2),'ro');
hold on
plot(Times2(indxy2),ay2(indxy2),'k*');
hold on
stem(Times2(locsy2),ay2(locsy2),'ro')
xlabel('time');
ylabel('ay');
subplot(212);
plot(Times2,az2,'b');;
hold on
plot(Times2(locsz2),az2(locsz2),'ro');
hold on
plot(Times2(indxz2),az2(indxz2),'k*');
hold on
stem(Times2(locsz2),az2(locsz2),'ro')
xlabel('time');
ylabel('az');ptime1 = Times2(locsy2);
ptime2 = Times2(indxz2);for i = 1:length(ptime1)-1diff1(1,i)=ptime1(i+1)-ptime1(i);diff2(1,i)=ptime2(i+1)-ptime2(i);
end
2*mean(diff1)
2*mean(diff2)
% figure;
% plot(ptime1-ptime2);p1=Times2(indxy2(4:end));
p2=Times2(indxz2);for i = 1:length(p1)-1diff1(1,i)=p1(i+1)-p1(i);diff2(1,i)=p2(i+1)-p2(i);
end
5*mean(diff1)
5*mean(diff2)ay=mean(sqrt(ax2(locsz2).^2 + ay2(locsz2).^2 + az2(locsz2).^2))
endif sel == 3
figure;
subplot(211);
plot(Times3,ay3,'b');
hold on
plot(Times3(locsy3),ay3(locsy3),'ro');
hold on
plot(Times3(indxy3),ay3(indxy3),'k*');
hold on
stem(Times3(locsy3),ay3(locsy3),'ro')
xlabel('time');
ylabel('ay');
subplot(212);
plot(Times3,az3,'b');;
hold on
plot(Times3(locsz3),az3(locsz3),'ro');
hold on
plot(Times3(indxz3),az3(indxz3),'k*');
hold on
stem(Times3(locsz3),az3(locsz3),'ro')xlabel('time');
ylabel('az');ptime1 = [100.685;101.31;101.89;102.666;103.198;103.794;104.343;104.918;105.308;105.865;106.536;] ;
ptime2 = [100.885;101.47;102.039;102.589;103.143;103.707;104.281;104.823;105.387;105.952;106.536;]; for i = 1:length(ptime1)-1diff1(1,i)=ptime1(i+1)-ptime1(i);diff2(1,i)=ptime2(i+1)-ptime2(i);
end
2*mean(diff1)
2*mean(diff2)
figure;
plot(ptime1-ptime2);p1=Times2(indxy2(4:end));
p2=Times2(indxz2);for i = 1:length(p1)-1diff1(1,i)=p1(i+1)-p1(i);diff2(1,i)=p2(i+1)-p2(i);
end
5*mean(diff1)
5*mean(diff2)
ay=mean(sqrt(ax3(locsz3).^2 + ay3(locsz3).^2 + az3(locsz3).^2))end

三、仿真结果

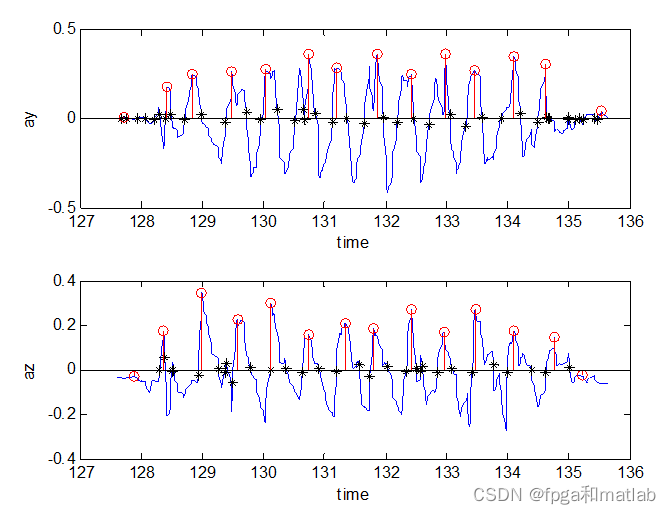
从图的仿真结果可知，通过峰值检测和过零检测算法，我们可以得到各个峰值以及过零点值，其具体数值结论如下：

对于峰值时刻，y轴的峰值检测时刻为：100.6850，101.3100，101.8900，102.6660，103.1980，103.7940，104.3430，104.9180，105.3080，105.8650，106.5360。z轴的峰值检测时刻为：100.8850，101.4700，102.0390，102.5890，103.1430，103.7070，104.2810，104.8230，105.3870，105.9520，106.5360。两个轴上峰值的检测时刻误差为： -0.2000，-0.1600，-0.1490，0.0770，0.0550，0.0870，0.0620，0.0950，-0.0790，-0.0870，0。那么由y轴加速度数据和z轴加速度数据，我们分别得到的步伐周期为1.1302s和1.1702s。由此可见，通过y轴和z轴计算的步伐周期之间存在一定的差异性。同理，根据过零点时刻数据，由y轴加速度数据和z轴加速度数据，我们分别得到的步伐周期为1.1091s和1.1629s。由此可见，通过y轴和z轴计算的步伐周期之间存在一定的差异性。