Python波动方程介绍：掌握物理模型与实际应用

在物理学中，波动方程是一种描述波动现象的数学模型。而在工程学中，波动方程也被广泛应用于声波、电磁波和弹性波等领域。Python是一种高效且易于学习的编程语言，因此被广泛用于模拟和分析波动方程。

Python波动方程的基本原理

波动方程可以表示出波的传播和变化规律，通常被用于描述一个无限长的弹性介质中的纵波和横波。其基本形式为：

$$\frac{{\partial }^{2}u}{\partial t^2}=c^2\frac{{\partial }^{2}u}{\partial x^2}$$

其中，$u$表示波的位移，$c$表示波速，$t$表示时间，$x$表示波动介质的位置。

在Python中，可以使用SciPy等库来模拟和求解波动方程，进而进行数据分析和预测。

Python波动方程在声波分析中的应用

声波是一种机械波，可以通过振动的媒介传输。在工程应用中，声波分析常常被用于检测声波信号、测量材料的弹性系数、以及掌握地球内部的结构信息。

Python中的波动方程可以被用于模拟声波在空气或水中的传播过程，进而预测声波的强度、传播距离和反射率等信息。这对于声波信号的检测和阐明其潜在应用场景具有重要意义。

Python波动方程在图像处理中的应用

Python波动方程在图像处理中的应用同样不可忽视。一般来说，图像可以看作是一种波动形式，其颜色和亮度等属性可以被视为波的振幅。因此，Python波动方程可以被用于模拟和分析图像的变化过程，进而增强图像的质量和效果。

结论

如此多样化且多领域的应用场景，表明了Python波动方程的重要性和普适性。百度、谷歌等搜索引擎均包括了丰富的Python波动方程介绍和分析，如中国知网发布的论文《Python在波动方程求解中的应用》等。如此，本文介绍了Python波动方程的基本原理和具体应用场景，希望能够给读者提供基础思路，也希望读者们在工作和学习中能够深入了解Python波动方程的潜力和局限性，进而在实践中发掘更多的应用前景。

最后的最后

本文由chatgpt生成，文章没有在chatgpt生成的基础上进行任何的修改。以上只是chatgpt能力的冰山一角。作为通用的Aigc大模型，只是展现它原本的实力。

对于颠覆工作方式的ChatGPT，应该选择拥抱而不是抗拒，未来属于“会用”AI的人。

🧡AI职场汇报智能办公文案写作效率提升教程 🧡 专注于AI+职场+办公方向。
下图是课程的整体大纲


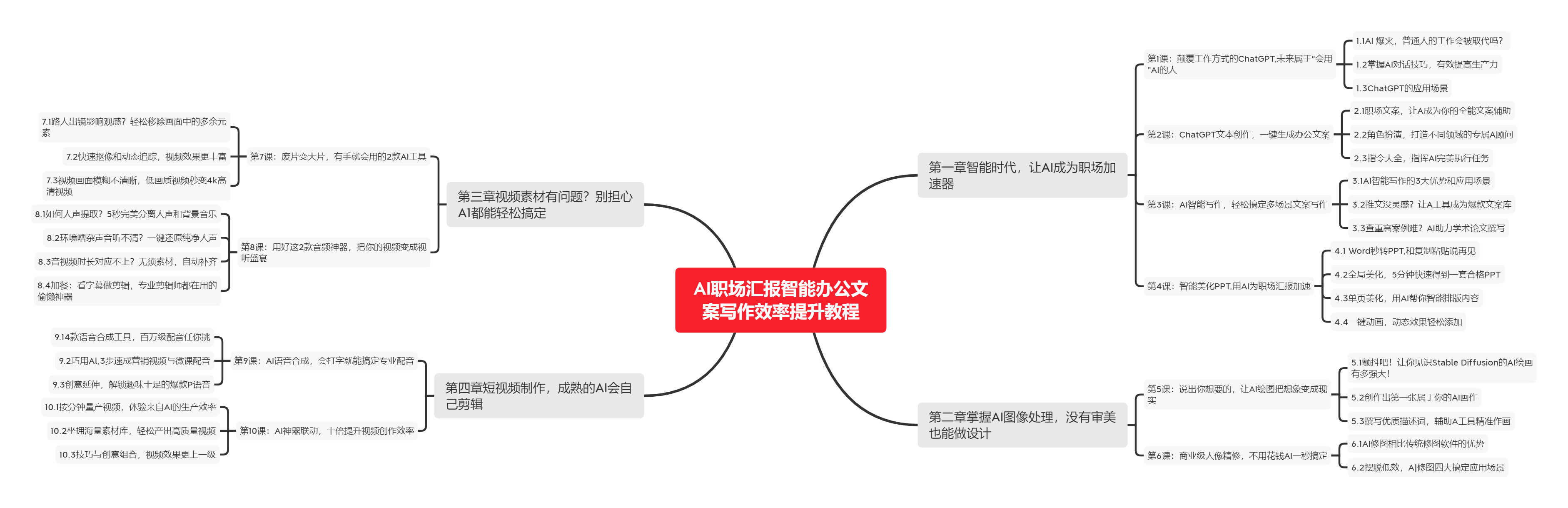
下图是AI职场汇报智能办公文案写作效率提升教程中用到的ai工具

🚀 优质教程分享 🚀

• 🎄可以学习更多的关于人工只能/Python的相关内容哦！直接点击下面颜色字体就可以跳转啦！

学习路线指引（点击解锁）	知识定位	人群定位
🧡 AI职场汇报智能办公文案写作效率提升教程 🧡	进阶级	本课程是AI+职场+办公的完美结合，通过ChatGPT文本创作，一键生成办公文案，结合AI智能写作，轻松搞定多场景文案写作。智能美化PPT,用AI为职场汇报加速。AI神器联动，十倍提升视频创作效率
💛Python量化交易实战 💛	入门级	手把手带你打造一个易扩展、更安全、效率更高的量化交易系统
🧡 Python实战微信订餐小程序 🧡	进阶级	本课程是python flask+微信小程序的完美结合，从项目搭建到腾讯云部署上线，打造一个全栈订餐系统。