#建模、预测和可视化
# 导入相关包
import numpy as np
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split # 切分训练集和测试集的函数import matplotlib
import matplotlib.pyplot as plt
matplotlib.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文标签
matplotlib.rcParams['axes.unicode_minus']=False # 用来正常显示负号
matplotlib.style.use('ggplot')# 构造数据
np.random.seed(0)
x = np.linspace(-10,10,100) # 从-10到10之间的100个等差数列
# 设置一个线性回归公式
y = 0.85*x - 0.72
# 创建一组数量为100,均值为0,标准差为0.5的随机数组
e = np.random.normal(loc = 0,scale = 0.5,size = x.shape)
# 将变量y加上这个变量e
y += e
plt.plot(y) # 数据折线图如下:
# 将x转换为二维数组,因为fit方法要求x为二维结构
x = x.reshape(-1,1)lr = LinearRegression()
# 切分训练集和测试集
x_train,x_test,y_train,y_test = train_test_split(x,y,test_size=0.25,random_state=0)# 拟合函数
lr.fit(x_train,y_train)
# 拟合后可利用lr.coef_和lr.intercept_来取出(w)权重和(b)截距
print('权重:',lr.coef_)
print('截距:',lr.intercept_)# 通过训练集得到了拟合函数,就可以进行预测
y_hat = lr.predict(x_test)
# 可查看对比实际值和预测值
print('实际值:',y_test)
print('预测值:',y_hat)# 将数据可视化
plt.figure(figsize=(10,5))
# 训练接和测试集都以散点来表示,拟合线用折线表示
plt.scatter(x_train,y_train,s=10,label='训练集',c='b')
plt.scatter(x_test,y_test,s=10,label='测试集',c='g')
plt.plot(x,lr.predict(x),label='拟合线',c='r')
plt.legend()
# 数据视图如下: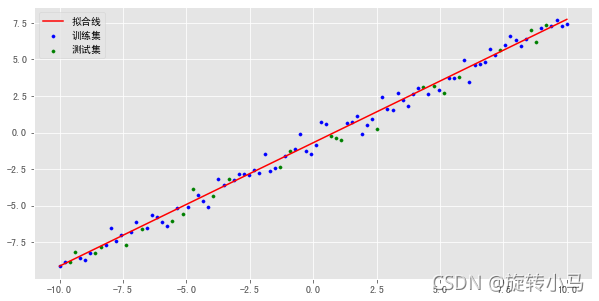
# 用图表示出实际值和预测值
plt.figure(figsize=(10,5))
plt.plot(y_test,label='真实值',c='r',marker='o')
plt.plot(y_hat,label='预测值',c='g',marker='x')
plt.legend()
# 数据视图如下: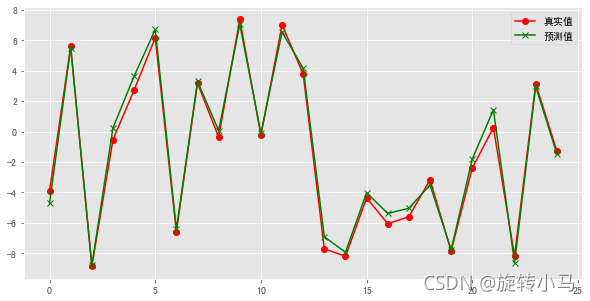
#模型评估
MSE:Mean Squared Error
平均方误差是指参数的估计值和参数的实际值之差的平方的期望,可以评价数据的变化程度,MSE越小,说明模型的拟合实验数据能力强。

RMSE :Root Mean Squared Error
根均方误差是均方误差的平方根。
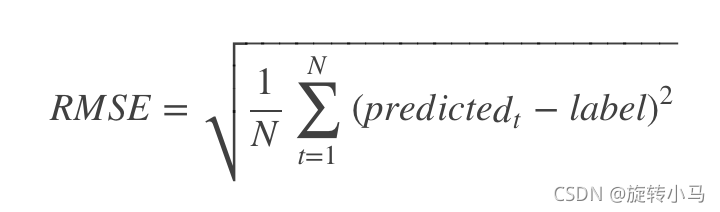
MAE: Mean Absolute Error
平均绝对误差是样本绝对误差的绝对值,能更好的反应预测值误差的实际情况。
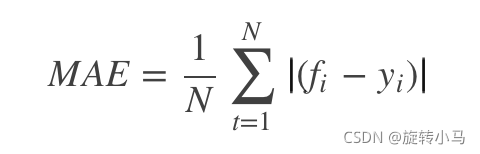
# 模型评估
from sklearn.metrics import mean_squared_error,mean_absolute_error,r2_score
print("平均方误差(MSE):",mean_squared_error(y_test,y_hat))
>>> 平均方误差(MSE): 0.2738537199293911print("根均方误差(RMSE):",mean_absolute_error(y_test,y_hat))
>>> 根均方误差(RMSE): 0.4374356584882062print("平均绝对值误差(MAE):",r2_score(y_test,y_hat))
>>> 平均绝对值误差(MAE): 0.9896372020590347参考链接:
python代码实现回归分析--线性回归 - 知乎
均方误差(MSE)根均方误差(RMSE)平均绝对误差(MAE)_lighting-CSDN博客