0. 写在前面

总导航在此

这些问题是我备考高等数学过程中，详细总结的常见面试问题和答案。逐个搜索并记录下来，花了很大的精力！

1. 泰勒展开和傅立叶变换的概念以及他们在计算机领域中的应用

泰勒展开可以用函数在某一点的各阶导数值做系数构建一个多项式来近似表达这个函数

泰勒展开可以帮我们在计算机中计算三角函数。因为计算机只会做加法（减法是加补码，乘法除法是移位），而三角函数是怎么求的呢？这就需要泰勒展开，把三角函数变成幂级数，计算机就能直接求加减乘除了。说简单的，泰勒展开能够把 质量高数量少 的运算变为 质量少数量多的运算，计算机不就喜欢运算次数多，但是不复杂的算式吗？

傅里叶变换的作用就是把非正余弦周期（请注意必须是周期函数）函数转化为无限个规则的正弦余弦函数。变成规则的函数以后，虽然有无限项，但是工程取前几项精度就够用了。

傅里叶变换在计算机领域中可以帮助我们进行图像去噪：设计一个低通滤波器(高斯函数)，去掉图像中的高频噪声

2. 傅里叶变换和傅里叶级数的区别

傅里叶变换的作用就是把非正余弦周期（请注意必须是周期函数）函数转化为无限个规则的正弦余弦函数。变成规则的函数以后，虽然有无限项，但是工程取前几项精度就够用了。

傅里叶级数就是也就是一系列的三角函数An sin(nωt+ψ)之和来表示的那个较复杂的周期函数f(t)

3. 函数零点和极值点怎么求

4. 判断两个无穷集合的大小，单射满射和双射的概念

对无限集，通过建立一一对应的方法可以比较它们元素个数的大小（在集合论中称为势），以整数集 Z ZZ 和偶数集 A AA 为例，如果将 Z ZZ 中的每一个元素都乘以 2 22，则都可以在 A AA 中找到对应的偶数元素，即 Z ZZ 和 A AA 中的元素是一一对应的，也就是说这两个集合是等势的。值得注意的是，偶数集合是整数集合的一部分，但它包含的元素个数却跟整数集合一样多。

单射满射和双射的概念这个非常易懂

https://blog.csdn.net/zjpp2580369/article/details/102462935

5. 欧式距离及其常见距离公式的缺点

https://blog.csdn.net/sinat_27652257/article/details/80483325

欧氏距离，最常见的两点之间或多点之间的距离表示法

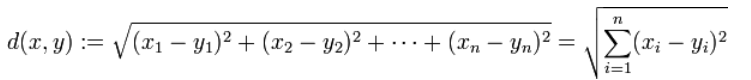
欧氏距离虽然很有用，但也有明显的缺点。它将样品的不同属性（即各指标或各变量量纲）之间的差别等同看待，这一点有时不能满足实际要求。例如，在教育研究中，经常遇到对人的分析和判别，个体的不同属性对于区分个体有着不同的重要性。因此，欧氏距离适用于向量各分量的度量标准统一的情况。

6. 什么是最大似然估计？

https://www.bilibili.com/video/BV1Hb4y1m7rE

最大似然估计，通俗解释：就是最可能的概率（回头想想例子中，就是我们通过幼儿园常识判断的最大可能的概率，只不过把大家常识通过数学公式呈现出来了而已）。数学解释：我们通过抽样得到一个样本值，通过样本值的数据，去推算取出某个样本的概率。（p的最大似然估计，只是p最大的可能性）

7. 梯度方向导数和梯度下降？

https://www.bilibili.com/video/BV1uZ4y1L7bB

方向导数公式👇：

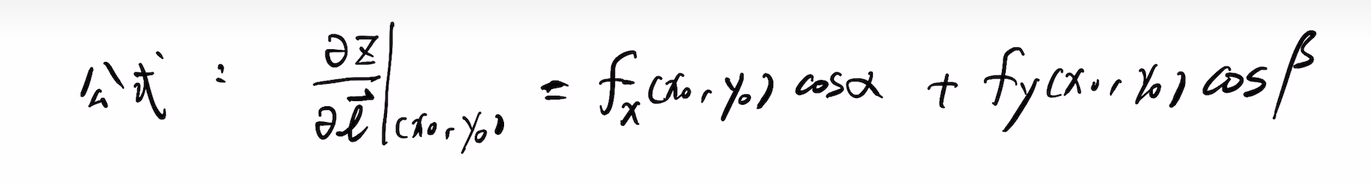
某个点在不同的方向有不同的方向导数，变化率最大的方向是哪个方向？就是该点梯度向量的方向。

8. 符合函数求导公式？给出函数让求？

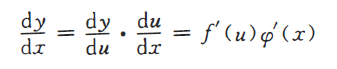
9. 倒数和偏导数的区别？

导数和偏导没有本质区别,都是当自变量的变化量趋于0时,函数值的变化量与自变量变化量比值的极限.一元函数,一个y对应一个x,导数只有一个.二元函数,一个z对应一个x和一个y,那就有两个导数了,一个是z对x的导数,一个是z对y的导数,称之为偏导.

10. 可微，可导，连续、可积的区别

对于一元函数有，可微<=>可导=>连续=>可积
对于多元函数，不存在可导的概念，只有偏导数存在。函数在某处可微等价于在该处沿所有方向的方向导数存在，仅仅保证偏导数存在不一定可微，因此有：可微=>偏导数存在=>连续=>可积。

11. 三个中值定理的区别连续和物理意义

首先提一下费马引理：极值点的导数为0，前提是可导

• 罗尔中值定理

• 拉格朗日中值定理

• 柯西中值定理

  ‘下面这个视频讲得是真的好，牛逼！真的全部一下就懂了

  https://www.bilibili.com/video/BV1AZ4y1G7Ub