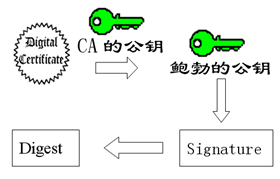
0x01 生成随机密钥
随机密钥可以大大增加密钥的安全性,生成随机密钥这里要用到随机数生成器(RNG),是一个用于生成随机数的程序或硬件
随机数在密码学的很多算法中都是必不可少的,如果某些算法的密钥不能采用随机生成的方式,就会带来很大的安全问题,例如通过某种规律,攻击者可以进行猜测,碰撞等得到明文
在随机数生成中,通常用熵来表示随机数的随机性
熵:指某些物质系统状态的一种量度,某些物质系统状态可能出现的程度
(希腊语:entropia,英语:entropy)的概念是由德国物理学家克劳修斯于1865年所提出。在希腊语源中意为“内在”,即“一个系统内在性质的改变”,公式中一般记为
随机数分类

真实随机数(TRNG)是理想化的随机,是没有一点规律可循的随机,但是非常难实现,《密码工程》书中提出,有人用按键的精确市场、鼠标的精确移动轨迹、按键时间等特性得到真实随机值,但是仔细分析也是存在差值的
伪随机数(PRNG)可以理解为利用随机种子生成的称为“真实随机数”的非真实随机数
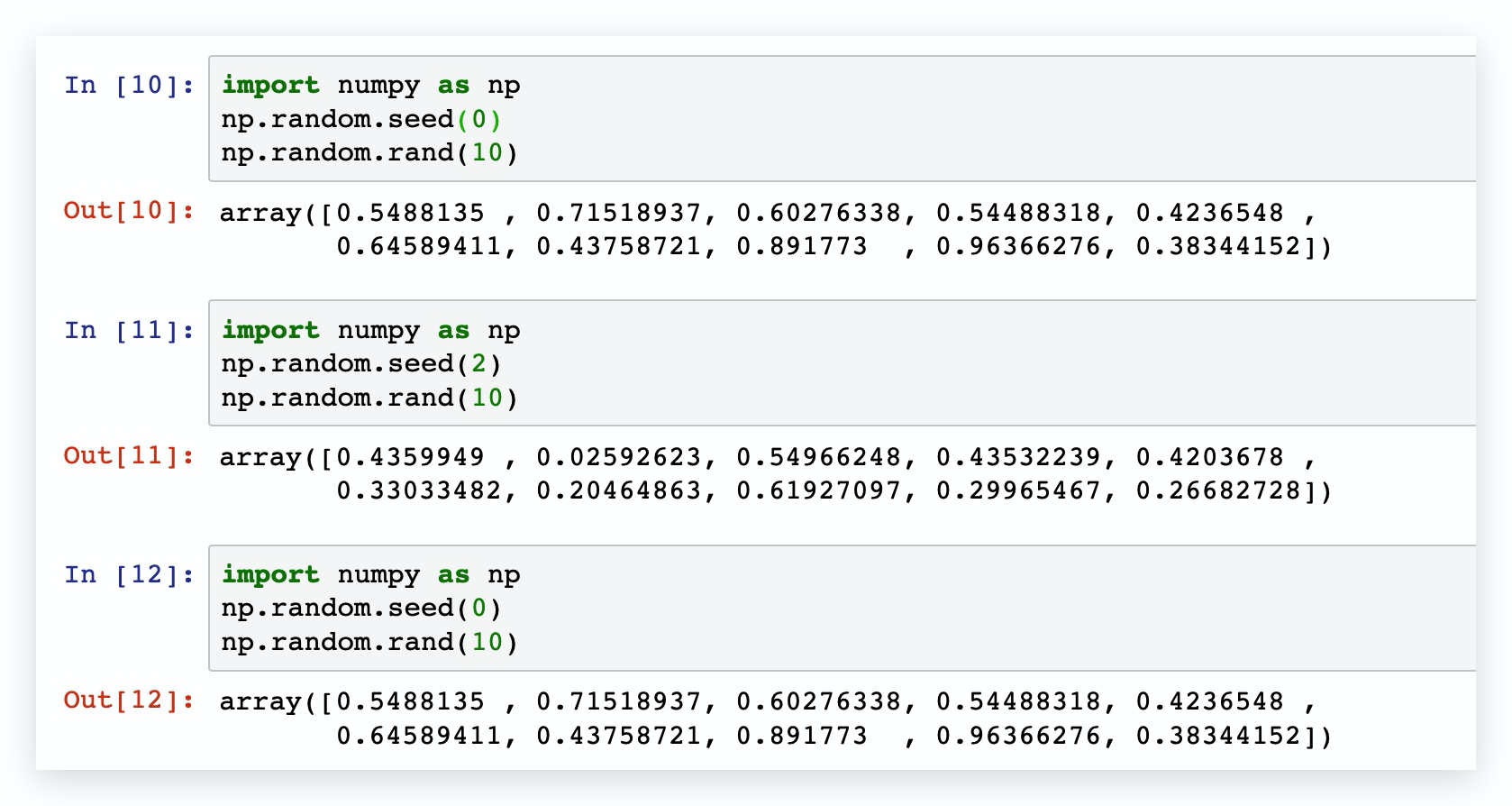
在很多算法中,设置相同的种子seed值,得到的随机数是相同的
累加器
累加器负责从不同的嫡源中获取实随机数,并用来更新生成器的种子
0x02 素数
质数同时又称为质数,早在刚认识到数字时,就了解到了素数的概念,质数是指在大于1的自然数中,除了1和它本身以外不再有其他因数的自然数
以下是百科给出的介绍
质数为无穷∞的推论
欧几里得的《几何原本》中有一个经典的证明,它使用了证明常用的方法:反证法
具体证明如下:
假设质数只有有限的n个,从小到大依次排列为p1,p2,……,pn,设N=p1×p2×……×pn,那么,是素数或者不是素数。
如果为素数,则要大于p1,p2,……,pn,所以它不在那些假设的素数集合中

《密码工程》中给出的三个素数引理
- 如果a|b且b|c,那么a|c
- 如果n为大于1的正整数且d为n除1之外最小的因子,那么d是素数
- (欧几里得)素数有无穷多个
其中a|b表示a整除b
素数特性
- 存在任意长的一段连续数,其中的所有数都是合数(相邻素数之间的间隔任意大)
证明:当0<a<=n时,n!+a能被a整除
长度为n-1的数列n!+2, n!+3, n!+4, …, n!+n中,所有的数都是合数
这个结论对所有大于1的整数n都成立,而n可以取到任意大 - 所有大于2的素数都可以唯一地表示成两个平方数之差。
证明:大于2的素数都是奇数
假设这个数是2n+1,由于(n+1)2=n2+2n+1,(n+1)2和n2就是我们要找的两个平方数。下面证明这个方案是唯一的。如果素数p能表示成a2-b2,则p=a2-b2=(a+b)(a-b)
由于p是素数,那么只可能a+b=p且a-b=1,这给出了a和b的唯一解 - 当n为大于2的整数时,2n+1和2n-1两个数中,如果其中一个数是素数,那么另一个数一定是合数
证明:2^n不能被3整除
如果它被3除余1,那么2n-1就能被3整除;如果被3除余2,那么2n+1就能被3整除。总之,2n+1和2n-1中至少有一个是合数
Eratosthenes筛选法
埃拉托色尼筛选法(Eratosthenes)简称埃氏筛法
是古希腊数学家埃拉托色尼(Eratosthenes 274B.C.~194B.C.)提出的一种筛选法,是针对自然数列中的自然数而实施的,用于求一定范围内的质数,它的容斥原理之完备性条件是p=H~
百科给出的详细的计算步骤如下
- 先把1删除(现今数学界1既不是质数也不是合数)
- 读取队列中当前最小的数2,然后把2的倍数删去
- 读取队列中当前最小的数3,然后把3的倍数删去
- 读取队列中当前最小的数5,然后把5的倍数删去
- 读取队列中当前最小的数7,然后把7的倍数删去
- 如上所述直到需求的范围内所有的数均删除或读取

address:https://bkimg.cdn.bcebos.com/pic/bd3eb13533fa828b84ab26eefd1f4134970a5a36
密码学的很多算法都用到了素数这个概念,在某些密码学算法底层使用过程中需要对密码学算法本身的参数进行运算
以下运算过程中,p为素数,进行运算的数为0...p-1
模运算
素数模运算的基本规则是,把模运算当作普通的整数运算,但是每一次的结果 r都要对p进行取模运算。取模运算非常容易:用p除r,去掉商,将所得的余数作为结果
加法 & 减法
两个数相加,如果结果大于或者等于p,就减去p
乘法
首先按整数乘法的规则计算ab的值,然后对结果做取模p运算。由于ab的最大可能值为(p-1)2=p2-2p+1,所以就需要执行一次长除法来找到满足ab qptr且0≤r<p的(q,r),去掉q,r 就是结果
素性测试
Miller Rabin是检验大数质数的一种快速方法。该算法称为Rabin-miller primality test
它决定数是否为素数,与Fermat primality Test 和 Solovay- Strassen primality test相同
这个检验是基于对质数成立的相等或一组相等,因此检查它们是否对数字成立,需要检验质数
该算法是目前已知最有用的一种素数测试算法,可以在不同的基于RSA加密的软件库中使用,最好的实例是OpenSSL
Miller Rabin验证了这个数字是合数,这叫做合数检验而不是质数检验,miller Rabin测试可以识别所有的和数,对于每个合数n,至少有3/4的数字a见证了n的合数
Miller Rabin是Fermats little Theorem的联想性简单扩展,使我们能够用比Fermats little Theorem大得多的概率来检验质数

References
《密码工程》
http://www.matrix67.com/blog/archives/234