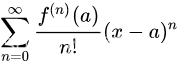考研一战顺利上岸啦，报考专业计算机科学与技术，考的数一英一。现在离开学还有段时间，所以趁机把自己的笔记都整理一下，希望可以帮到一些备考的同学。

写在前面：

1. 首先说一下自己的复习计划跟想法。数一今年有点难，我也考得不是很高分，不过我也总结了一些不足之处，或许会有帮助。
   我看的网课是：汤家凤高数基础班+李永乐线代+张宇高数/概率论强化班。
   使用的教材是：课本+汤家凤1800+李永乐线代+张宇高数18讲+张宇概率论9讲。
   
   (1) 前期打基础阶段：我跟的是汤神的基础班，收获很多，这个阶段算是对数学从一个遗忘到熟悉的过程。
   个人看课的流程就是(请勿模仿)：看网课，看课本，做课本习题。看完全部基础课之后，又开始做1800基础题。这个过程花的时间实在太多了，网上说是打基础多花点时间没关系，但是效果实在不大。
   我个人的建议是在课本习题跟1800的基础题两者之中选一个做就好了。至于1800的强化题，我感觉不是很有必要做，直接进入教材的强化阶段就好。
   
   (2) 暑期强化阶段：一般暑期就要进入强化阶段了，这个阶段需要使用教材，比如高数18讲、闭关修炼之类的(这两个也是我用的)。我看的是张宇老师的强化课，课不多，宇哥讲得生动，所以听起来还蛮有趣的。
   这个阶段是我把各个知识点深入理解或牢牢记住的过程。说实话，收获是有的，基础夯实了很多，也跟着宇哥学到了一些巧妙的解法。
   但是后期做真题的时候，感觉自己的基础还是不够。所以如果重来一次的话，我可能会选择做复习全书跟660，抱紧永乐大帝大腿。
   
   (3) 真题阶段：10月份左右要开始真题，刷完之后开始模拟题，模拟题我只做了李林的，最后一道也没押到，血亏，如果重来我绝对不选李林。
   真题部分我也做了一点总结，后续再整理在另一篇博客里。
   
2. 这些笔记是我在复习时总结的，适合有点基础的同学复习或者查漏补缺阅读。因为我没有将笔记记得十分详细，大多数是标记一些个人觉得重要的知识点，以及对部分难点的个人想法，建议使用ctrl+f 有针对性地查找、阅读。
3. 笔记中的“18讲”指张宇高数18讲。

一、外部资料

这部分是一些我收集的网上的学习资料，当初看到的时候觉得可能会用到，所以一直保存着。不过后来发现我连教材都看不完(残念~)。

1. 待定系数法：https://baijiahao.baidu.com/s?id=1611637003912949194&wfr=spider&for=pc
2. 高数吧-极限知识总结：
   https://tieba.baidu.com/p/5906863580?pid=122340965240&cid=&red_tag=0525843440#122340965240

二、笔记正文

1. 判断有界：若定义域内有界，除了间断点处，还要考虑趋于定义域边缘时的情况，见18讲例2.7；
2. 利用定积分求极限：（$i$从0累加到$n$）努力凑出$i/n$（作为$x$）和$1/n$（作为$dx$），见18讲例2.9.（3）；
3. 负数移入根号内时注意符号，如果是求极限或者积分建议直接换元，见18讲例2.15；
   【注：当$x＜0$时，要使用代换$t=-x$化为常见的情况，或用$-x$同时除分子、分母，这样才不会出现正负上的错误。】
4. $lnt$跟$1/t$在同个式中使用洛必达时，注意$lnt$在分子，$1/t$在分母，见18讲例2.17；
5. 使用等价无穷小代换的条件：分子分母均为等价无穷小；
6. $1^{\infty }$型：$lim{u}^v=e^{lim[(u-1)v]}$；
7. 利用泰勒公式确定式子中参数的值：题中给出的高阶无穷小是第几项就泰勒展开到第几项，比如给出$o(x^3)$，就展开$e^x=1+Ax+B{x}^2+C{x}^3+o(x^3)$，讲18讲例2.33；
8. 无穷小量的0次方等于1，见18讲例2.8；
9. 高数18讲第2讲习题摘抄：2.1、2.8；
10. 计算极限时，可以使用无穷小相加的公式，见闭关修炼1.1.7；
11. 计算抽象型函数极限时注意放缩，见闭关修炼例1.1.30；
12. 闭关修炼第1讲习题摘抄：1.1.30、1.1.33、1.1.41、1.1.44 ~ 1.1.49、1.1.53；
13. 脱帽 & 戴帽；
14. 多项相乘时，把点代入，看看哪一项的值跟其他项不同；
15. 方程难解时考虑转换成对数或者其他形式进行求解。
16. 微分的线性主部：研究的整体求导才是A，见闭关修炼例1.2.15；
    函数在点$x_0$可微，记$ dy = AΔx$ ，称为函数的微分，又称为函数的线性主部。
17. 需要求出隐函数的解时，多尝试画图，见闭关修炼例1.2.19；
18. 记住结论：设$f(x)$在$x=a$处连续，$F(x)=f(x)|x-a|$，则$f(a)=0$是$F(x)$在$x=a$处可导的充要条件，见闭关修炼例1.2.11；
19. 十字相乘法：十字左边相乘等于二次项系数，右边相乘等于常数项，交叉相乘再相加等于一次项系数，最后要横写因式，见闭关修炼例1.2.31；
20. 求极限时及时提出常数，见闭关修炼例1.2.22(2)；
21. 注意数形结合题，极值点是一阶导数正负改变，拐点是一阶导数单调性改变，见闭关修炼例1.2.55；
22. 判别极值&拐点的第三充分条件，见18讲P83~P84；
23. 求三点时注意不可导的点！
24. 就算函数在定义域上单调递增，求范围时也应该求上限，即求x趋于正无穷的极限；
25. 求开区间上的最值时，要求函数趋于端点的极限；
26. 高数18讲第3讲习题摘抄：例3.8；
27. 去掉根号跟绝对值要注意符号，具体根据题意进行判断，有必要时需要画图，见闭关修炼1.2.67；
28. 拐点是一个点，要写成$(x,y)$的形式，见闭关修炼1.2.52；
29. 同一方向上水平渐近线与斜渐近线不可并存；
30. 若用某一条曲线在某点代替另一条曲线，则在该点处，两条曲线函数值相同、斜率相同、曲率相同，见闭关修炼1.2.64；
31. 高数18讲第4讲习题摘抄：例4.1、例4.3*、例4.5* ~ 4.7*(两个未知数求解只需要两个方程)；
32. 带拉格朗日余项的一阶泰勒公式：这里的阶数不包括余项；
33. 薄弱的知识点*：中值定理（难点）、微分不等式、积分等式&不等式、多元微分学-隐函数存在定理、多元微分学-隐函数求导（什么时候不能用公式法）、多元微分学-极值判别方法失效的处理方法、多元微分学-判断偏导数连续、二重积分计算、二重积分求导、常微分方程的应用（原理不难，多做题熟悉）、第一型曲线积分&第一型曲面积分；
34. 需要背诵的公式：求导公式、基本积分公式、三角函数、曲率公式、高阶求导公式、泰勒公式、基本不等式、绝对值不等式、经典不等式(18讲第6讲)、有理函数积分的原则、定积分区间简化公式、弧长&扇形公式、数量积&向量积&混合积及其几何意义、线&面方程及其切向量、角度(线线、面面求得的都是cos，线面为sin)与距离的求法(点到直线)、梯度&方向导数&散度&旋度(平面上的旋度：格林公式)、一二型曲线曲面积分相关公式、曲线(切向量)&曲面(法向量)、傅里叶级数相关公式；
35. 
36. 高数18讲第5讲习题摘抄：例5.3、例5.4、例5.8 ~ 5.9、例5.14 ~ 5.17*、例5.23(保号)、习题5.2、5.5、5.7；
37. 任何实系数奇次方程至少有一个实根，见18讲P111；
38. 高数18讲第6讲习题摘抄：例6.2、例6.6、例6.12、习题6.4；
39. 定积分的几何意义，若为x轴下方的图形，注意得从a到b（即按顺序）才是负数。
    【18讲原文：若$f(x)<0$，曲边梯形就在x轴下方，定积分的绝对值仍等于曲边梯形的面积，但定积分的值是负的。】
40. 闭关修炼第2讲习题摘抄：1.2.2、1.2.5、1.2.9*、1.2.16(2)、1.2.31*、1.2.23、1.2.33、1.2.36、1.2.53、1.2.57、1.2.64、1.2.67、1.2.70、1.2.74 ~ 1.2.74、1.2.77 ~ 1.2.79、1.2.81、1.2.85 ~ 1.2.88、1.2.90、1.2.93；
41. 判断函数是否具有原函数：1）连续必有原函数；2）看间断点类型，除了振荡间断点，其他都没有原函数。
42. 判断函数是否有定积分：1）连续必有定积分；2）有原函数，有界；
43. 连续的偶函数$f(x)$的原函数中仅有一个原函数为奇函数，当 ${\int }_0^{a}f(u)du=0$，证明见18讲例7.6；
44. 求定积分，根号中最高项为平方项时，注意配方法，见18讲例7.49；
45. 换元时要注意上下限有无超出界限，但一般来说不用过分在意细节，见18讲例7.28；
46. 原函数如果是奇函数，则反函数也是奇函数。原函数是非奇非偶函数，则反函数也是非奇非偶函数。原函数是偶函数的话，则没有反函数。
47. 高数18讲第7讲习题摘抄：例7.15 ~ 例7.16、例7.20、例7.29、例7.41、例7.55、习题7.6、习题7.13、习题7.17、习题7.21；
48. 复习表格积分法；
49. 计算参数方程的定积分，考虑使用换元法，见闭关修炼1.3.98；
50. $y_n=(1/n)\ast sin(nx)$在0到2π上的弧长与n无关，是个定值，见1.3.121；
51. 物理应用时注意位移距离；物体与水的密度相同，在水下不做功；
52. 曲线$y=y1(x)>=0$与$y=y2(x)>=0$及$x=a，x=b(a<b)$所围成的平面图形绕x轴旋转一周得到的旋转体体积：公式里是$y_1(x)$的平方减去$y_2(x)$的平方，不是和平方，见18讲P163；
53. 高数18讲第8讲习题摘抄：例8.6(强行结合极限)、例8.8、例8.3(二次函数的两点式方程)；
54. 闭关修炼第3讲习题摘抄：1.3.2、1.3.5*、1.3.8、1.3.12、1.3.14 ~ 1.3.15*、1.3.18(熟记广义反常积分)、1.3.21*、1.3.23*、1.3.25*(倒代换)、1.3.33(熟记有理积分原则)、1.3.35、1.3.52(换元得出对称区间，利用几何性质求定积分)、1.3.55 ~ 1.3.56、1.3.64、1.3.65*(原函数关系) ~ 1.3.67、1.3.76 ~ 1.3.78、1.3.81、1.3.94 ~ 1.3.96(注意审题)、1.3.98 ~ 1.3.99、1.3.110(2)、1.3.112、1.3.118、1.3.120* ~ 1.3.122*、1.3.124*、1.3.125 ~ 1.3.127**、1.3.128、1.3.131**、1.3.137；
55. 无论z对谁求导，也无论z已经求了几阶导，求导后的新函数仍然具有与原函数完全相同的复合结构；见18讲P187；
56. 若函数$z=f(x,y)$的二阶偏导数$f_{xy}^{\prime \prime }(x,y)$，$f_{yx}^{\prime \prime }(x,y)$在点$P_0(x_0,y_0)$处都连续，则$f_{xy}^{\prime \prime }(x_0,y_0)=f_{yx}^{\prime \prime }(x_0,y_0)$；
57. 高数18讲第10讲习题摘抄：例10.3、例10.8*(偏微分方程)、例10.13、例10.14、例10.17(判别方法失效例子)、例10.18 ~ 例10.19、习题10.1、习题10.3*(验证极限不存在：使用$y=kx$；若验证存在则不能这样使用；)、习题10.11 ~ 10.13；
58. 泰勒级数&幂级数(暂且这样理解)：泰勒展开是幂级数展开的有限版，幂级数是泰勒展开的无穷版；
59. 闭关修炼第4讲习题摘抄：1.4.2、1.4.4*、1.4.5(D选项混淆了一元函数极限与一阶偏导连续的概念)、1.4.7、1.4.14(第2小问注意多层复合求导)、1.4.18 ~ 1.4.22**(多元泰勒公式)、1.4.26、1.4.30(偏增量定义，△x的高次方视为△x的高阶无穷小，不用在意)、1.4.32(微分方程不够熟练)、1.4.44**、1.4.35*；
60. 轮换对称性：若把x与y对调后，区域D不变（或区域D关于$y=x$对称），则$\int {\int }_{D}f(x,y)dxdy=\int {\int }_{D}f(y,x)dxdy$，这就是轮换对称性；
61. 二重积分：在极坐标下，几乎所有的计算都是先积r，后积θ；
62. sgn函数的定义、根号$x^2+a^2$：见18讲例11.13；
    
63. 二重积分的中值定理：设$f(x,y)$在有界闭区域D上连续，${\sigma }_0$是D的面积，则在D内至少存在一点，使得
    
64. 高数18讲第11讲习题摘抄：P209注例1 ~ 注例2、例11.2*、例11.4*、例11.8、例11.11*** ~ 例11.18***、例11.21 ~ 例11.25*、习题11.8、习题11.10；
65. 闭关修炼第5讲习题摘抄：1.5.5、1.5.11、1.5.14、1.5.15、1.5.18、1.5.20 ~ 1.5.21；
66. 解微分方程要大胆展开，看到$dy/dx$；
67. 解齐次型微分方程时要注意对数函数的定义域，在计算过程中，若出现$ln(u)$，且u不知正负，一律加绝对值，见18讲例12.6；
68. 18讲P227注：分母不为0可能为导致丢解，但《考试大纲》只要求求出通解，并不要求求出全部解；
69. $\int [1/(1+sinx)]dx$：利用平方差公式化简；
70. 高数18讲第12讲习题摘抄：例12.1、例12.12 ~ 12.15、习题12.1、习题12.2(圆形区域化为其次方程再求导)、习题12.4；
71. 闭关修炼第6讲习题摘抄：1.6.1*(结合微分定义)、1.6.5 ~ 1.6.6、1.6.11*、1.6.13、1.6.15、1.6.22(注意符号问题)、1.6.240；
72. 点到空间直线距离：已知直线L与点M：（1）求出空间直线的方向向量s，找出一个直线上的具体点M0；（2）利用向量积定义求出$M{M}_0$与直线的夹角$sin\theta$，M到L的距离即$M{M}_0\ast sin\theta$；
73. 直线与平面的交点：利用参数方程；
74. 直线L在面π上的投影：过L且与π垂直的平面、与π的交线就是L在π上的投影线$L_0$；
75. 曲线在坐标面上(比如yOz)的投影曲线：消去对应项(x)即可；
76. 求曲线绕轴旋转所得的曲面方程：（1）写出轴的方向向量s，在轴上选一点$M_0$ [具体值]，在纬圆（曲线）上选一点$M_1(x_1,y_1,z_1)$ [不要取具体值]和点$P(x,y,z)$；
    （2）利用关系：$M_{1}P\perp s，|M_0{M}_1|=|M_{0}P|$，构造方程，把$x_1$,$y_1$,$z_1$按照关系替换成对应的xyz；
77. 将空间曲线化为参数式方程：（1）投影到适当的坐标平面，写出对应投影曲线的参数方程
    （2）将得到的参数方程回代到原方程中，得到另一个坐标的参数式写法；
78. 高数18讲第16讲习题摘抄：例16.4、例16.6*、例16.11* ~ 16.13*、例16.16 ~ 16.17、例16.20*、例16.22、例16.25、习题16.4、习题16.7、习题16.11 ~ 16.13；
79. 证明空间曲面是柱面：可以转换成证明该曲面任一点的法向量与一定直线垂直；
80. 欲求母线平行于z轴的柱面方程，只需求出xOy平面上的准线方程即可，而此准线就是C在xOy平面上的投影曲线，见18讲习题16.4；
81. 问函数在哪个方向取得最大的方向导数时，方向用角度表示；
82. 求函数在空间某一点的最大变化率：即求梯度的模；
83. 三重积分(实心)、一型面 & 二型面(空心)、一型线 & 二型线(通常由切面切而得到)；
84. 高数18讲第17讲习题摘抄：例17.7 ~ 例17.10(此部分的题目计算较复杂，可以适当通过积分的可加性进行拆分逐一解决)、例17.11 ~ 例17.15、习题17.11、习题17.16；
85. 估计三重积分的值，联想到被积函数的最值问题；
86. 三重积分：几何意义是体积，求法按照先一后二或先二后一；
87. 第一型曲线积分：一投二代三计算，将被积函数的变量全部换成某一个，dxdy这些也要变；
88. 第一型曲面积分：一投二代三计算，投影到某个平面形成二重积分，注意投影的平面不要出现重点；
89. 重心 = 形心，当题干出现密度均匀时，三心(前面两者加上质心)相同；
90. 第二型曲线积分：（1）直接计算，参数方程时投到t上，注意范围是从起点到终点；
    （2）格林公式：i：不封闭就补线；ii：存在奇点就挖去奇点，即圈出一条新的曲线，可以把分母设为挖去的奇点区域；
91. 第二型曲面积分：（1）直接计算法，分别投影到三个平面，如dydz投影到yOz平面；（2）转换成同个平面，转换关系：$dydz/-Z_x^{\prime }=dzdx/-Z_y^{\prime }=dxdx/1$，具体见18讲P377；[转换坐标变量法并非常用的方法，视曲面方程而定，如果给定曲面为平面、旋转抛物面等简单情况，可以考虑，原话见18讲P379；]（3）利用法向量转换成第一型曲面积分；以上转换注意符号正负；
92. $e^t+e^{-}t$：
    
93. 高数18讲第18讲习题摘抄：例18.3(不能拆成x与y方向，直接投成x计算)；例18.5 ~ 例18.6、例18.8(注意投影重点问题)、例18.11、习题18.3* ~ 习题18.4、习题18.7；
94. 平面束：明确不是哪一个面就让那个面乘以λ，另一个面的系数为1；
95. 最大变化率：
96. 方向余弦角度的范围：0~π；
97. 成反比：$y=k\ast (1/x)$;
98. 第二型曲线积分求原函数：利用格林公式两边相等构造出常微分方程，或者采用折线法化成定积分求解；
99. $z=sqrt(x^2+y^2)$：这个圆锥上任意一过顶点的直线和Z轴夹角相等，那就取$Y=0，Z^2=X^2，Z=X$，则圆锥与Z轴45度；
100. 闭关修炼第8讲习题摘抄：1.8.2、1.8.4、1.8.11、1.8.16、1.8.18、1.8.21、1.8.27、1.8.29 ~ 1.8.34、1.8.40**、1.8.45* ~ 1.8.47*(看到dV = 0.9S，先想办法写出V跟S的函数)、
     1.8.48(向量OP=(x,y),F⊥OP即相乘斜率为-1，故向量F=±(-y,x)，又因为夹角和y正向为锐角，根据P(X,Y)知，x＞0，y＞0，-(-y,x)=(y,-x)在第四象限和y轴正向为钝角舍去，(-y,x)在第二象限满足提体题意，故F=-yi+xj)、
     1.8.50(看不清楚L是什么曲线，化成极坐标就看清楚了)、1.8.58 ~ 1.8.59(关于选点：在x>0，即给定范围内任取一点，最好取有一个坐标为0的点)、1.8.60* ~ 1.8.61*、1.8.64 ~ 1.8.66、1.8.67(锐正钝负)、1.8.68、1.8.70(注意球面积分法φ的范围)、1.8.74；
101. 无穷级数敛散性判别：必要条件、充要条件、p级数、等比级数；（1）正项级数：比较审敛法、比较审敛法的极限形式、比值审敛法、根值审敛法；（2）交错级数：莱布尼茨判别法；（3）任意项级数：绝对收敛 & 相对收敛，绝对收敛必收敛；
102. 判断级数审敛性的时候，先判断级数类型(正项级数还是其他)；
103. 当$x＞0$时，有$x＞ln(1+x)$，所以对于任意正整数n，显然也有$1/n＞ln(1+1/n)$；
104. 正项级数审敛结论：（1）
     
105. 收敛级数的性质：（1）收敛级数的项任意加括号后所得的新级数仍收敛，且其和不变；（2）逆否命题：若加括号后的新级数发散，则原级数必然发散；（3）若加括号后得到的新级数收敛，不能断言原级数一定收敛；（4）绝对收敛的级数具有可交换性；
106. 三角公式：$sin(\alpha +n\pi )=(-1{)}^n\ast sin\alpha$；
107. 正项级数只谈收敛和发散，当正项级数收敛时是没有绝对收敛和条件收敛之分的；
108. 幂级数的收敛域：（1）具体型；（2）抽象型；见18讲P264；
109. 幂级数求和函数的突破口：（1）当$(an+b{)}^c$ 在分母上时，先导后积；（1）当$(an+b)^c $在分子上时，先积后导；
110. 约定$x^0=1$；
111. 等比级数的和 = 首项/(1 - 公比)，只要公比的绝对值＜1；
112. 高数18讲第13讲习题摘抄：例13.6 ~ 例13.8、例13.14、例13.16、例13.25*、习题13.1、习题13.5、习题13.12 ~ 13.13；
113. 泰勒展开就是幂级数，幂级数就是泰勒，因为幂级数展开具有唯一性；
114. 无穷级数：始终不要忘记在解题过程中标注收敛域；
115. 闭关修炼第7讲习题摘抄：全部；
116. 傅里叶级数：（1）狄利克雷收敛定理；（2）记住公式，求傅里叶系数，即$A_0$、$a_n$、$b_n$；（3）正弦级数与余弦级数；（4）延拓：将补充定义的手段叫做延拓；
117. 高数18讲第14讲习题摘抄：例14.16；

三、题型整理：

极限：求极限（根据定义or常规方法、注意数列求极限）、判断函数有界&连续&可导&极值&最值、给定极限求参数or其他函数的极限、无穷小阶数比较、连续性与间断点、数列极限收敛的充要条件、证明极限存在、证明方程仅有一个实根、综合题总结（闭关修炼P14：导数、积分、中值定理、方程列、区间列、极限）；

一元微分学：判断导数可导or可微、求导数or微分、求高阶导数、切线&法线&截距(可正可负)&单调性&极值&最值&凹凸性&曲率&渐近线、结合中值定理证明题、不等式问题、求方程的根or函数零点；

一元函数积分学：判断原函数奇偶性&周期性、积分比大小、定积分定义与极限联系、反常积分判敛&计算、定积分计算、变限积分求导与计算、与中值定理结合的积分等式与不等式问题、几何应用&物理应用；

二重积分：和式极限、积分比大小、计算二重积分(通常需要极直转换or变换积分次序)、二重积分的应用(面积、体积、质量、三心、转动惯量)；

微分方程：解微分方程通解&特解、与应用结合构造微分方程求解；

四、背诵公式整理：

1. 绝对值函数：18讲P7；
2. 等价无穷小、因式分解：闭关修炼P4 ~ P5；
3. 泰勒公式 & 泰勒级数（其实是同个东西）：闭关修炼P20；
4. 不等式：闭关修炼P12；
5. 基本不等式：
   
   
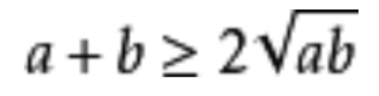
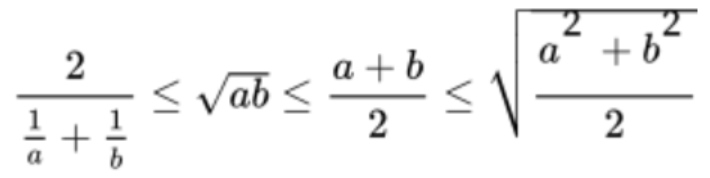
6. 无穷小的运算：18讲P29；
7. $1^{\infty }$公式：$lim(u^v)=e^{lim[(u-1)v]}$，18讲P43；
8. 取整函数的夹逼不等式：18讲P45；
9. 基本求导公式：闭关修炼P18；
10. 泰勒求高阶导数：闭关修炼P21例题；
11. 高阶导数重要公式：18讲P64；
12. 渐近线：闭关修炼P15；
13. 判断根的个数：闭关修炼P32；
14. 导数祖孙三代关系：18讲P67；
15. 一元积分学：周期函数公式：闭关修炼P38；
16. 定积分定义：基本形&放缩形&变量形：闭关修炼P40；
17. 定积分重要公式总结(区间简化公式)：闭关修炼P48；
18. 原函数(不定积分)存在定理：18讲P123；
19. 积分等式与积分不等式；
20. 多元函数微分学可微连续关系图：闭关修炼P68；
21. 多元函数泰勒公式&极值：闭关修炼P69；
22. 判断可微：18讲P186；
23. 二重积分和式极限：闭关修炼P72；
24. 二重积分各种对称：注意关于原点对称与关于y=x对称，闭关修炼P73；
25. 二重积分换元法：闭关修炼P80；
26. 二重积分定x，y的上、下限时，必须保证下限小、上限大，这是由其定义规定的；而累次积分并无此要求，18讲P215；
27. 高阶常系数微分方程通解&特解公式：18讲P230；
28. 韦达定理；
29. 用换元法求解微分方程：闭关修炼P86，没有给出方法，见例题；
30. 改变级数任意有限项，不会改变该级数的敛散性；
31. 收敛级数的性质：18讲P248；
32. 幂级数&幂级数相等&幂级数的四则运算性质：18讲P251；
33. 几何级数：18讲P254；
34. 求和函数突破口：18讲P266；
35. 比较判别法的4个尺度：闭关修炼P92；
36. 判敛常用结论：闭关修炼P94；
37. 抽象型判敛：闭关修炼P97；
38. 狄利克雷&傅里叶的公式：闭关修炼P100；
39. 重要的距离公式：18讲P323；
40. 旋转曲面：18讲P325；
41. 直线在面的投影：18讲P332；
42. 方向导数&梯度&散度&旋度：闭关修炼P109；
43. 球面坐标法：18讲P347；
44. 椭圆面积计算公式：18讲P357；
45. 两类曲面积分的关系与转换坐标变量法：18讲P377；
46. 高斯公式&斯托克斯公式；

四、写在最后

以上就是我在复习高数过程中的心得啦~看到这里不容易，希望上面的东西能对您有所启发，最后祝大家考研顺利！