小程一言
这篇文章是在排序进行曲1.0之后的续讲,
由于在上一篇讲的排序的基本概念与分类,所以这篇主要是对几个
简单的排序进行细致的分析,有直接插入排序、希尔排序以及堆排序。
直接插入排序
直接插入排序是一种简单直观的排序算法,它的基本思想是将待排序的元素依次插入到已排序的序列中的合适
位置,从而逐步形成有序序列。
步骤
1、将待排序的元素序列分为已排序区和未排序区。一开始已排序区只有一个元素,就是待排序序列的第一个元素。
2、从未排序区取出第一个元素,将其与已排序区的元素逐个比较,找到合适的位置插入。
3、比较的过程是从已排序区的最后一个元素开始,如果该元素大于待插入元素,则将该元素后移一位,直到找到一个小于等于待插入元素的元素位置。
4、将待插入元素插入到找到的位置后,已排序区的元素个数加一。
5、重复步骤2~4,直到未排序区的元素全部插入到已排序区。
举例
原始序列:5 3 8 6 4第一轮插入:3 5 8 6 4第二轮插入:3 5 6 8 4第三轮插入:3 4 5 6 8通过例子可以看出,直接插入排序每次将一个元素插入到已排序序列中的合适位置,通过不断地插入操作,最终将序列排序完成。
复杂度分析
直接插入排序的时间复杂度为O(n^2),其中n是待排序序列的长度。直接插入排序的最好情况时间复杂度为O(n),即当待排序序列已经有序时,只需要比较n-1次即可完成排序。最坏情况时间复杂度为O(n^2),即当待排序序列逆序排列时,需要比较和移动的次数最多。平均情况下,直接插入排序的时间复杂度也是O(n^2)。直接插入排序的空间复杂度为O(1),即只需要常数级别的额外空间。直接插入排序是一种稳定的排序算法,即相等元素的相对顺序在排序前后不会改变。
应用场景
小规模数据排序:直接插入排序对于小规模的数据排序效果较好,因为它的时间复杂度为O(n^2),在数据规模较小的情况下,其性能优于其他复杂度较高的排序算法。例如,对于一个包含100个元素的数组进行排序,直接插入排序的效率较高。部分有序数据排序:如果待排序的数据已经部分有序,即每个元素距离它的最终位置不远,那么直接插入排序的效果会很好。这是因为直接插入排序每次将一个元素插入到已经有序的部分中,插入的操作比较快速。例如,对于一个近乎有序的数组进行排序,直接插入排序的效率较高。数据量较小且基本有序的在线排序:直接插入排序可以在不断接收新数据的情况下,实时对数据进行排序。例如,一个在线的股票交易系统,需要对新到达的交易数据进行排序,直接插入排序可以满足实时性的要求。
实际举例
假设有一个学生成绩的数组,需要按照成绩从低到高进行排序。可以使用直接插入排序来实现。首先,将第一个元素视为有序的部分,然后从第二个元素开始,逐个将元素插入到已经有序的部分中。具体的操作是,从第二个元素开始,将其与已经有序的部分比较,找到合适的位置插入,然后再将下一个元素插入,直到所有元素都被插入完成。这样就可以得到按照成绩从低到高排序的数组。
代码实现
public class InsertionSort {public static void main(String[] args) {int[] arr = {5, 2, 8, 3, 1};insertionSort(arr);for (int num : arr) {System.out.print(num + " ");}}public static void insertionSort(int[] arr) {int n = arr.length;for (int i = 1; i < n; i++) {int key = arr[i];int j = i - 1;while (j >= 0 && arr[j] > key) {arr[j + 1] = arr[j];j--;}arr[j + 1] = key;}}
}

希尔排序
希尔排序(Shell Sort)是插入排序的一种改进算法,也被称为缩小增量排序。希尔排序通过将待排序的元素按照一定的间隔分组,对每组进行插入排序,然后逐渐减小间隔,直到间隔为1时进行最后一次插入排序。
步骤
1、初始化间隔gap的值为数组长度的一半,然后不断将gap缩小为原来的一半,直到gap为1。
2、对于每个gap,将数组分为gap个子序列,分别对每个子序列进行插入排序。
3、在每个子序列中,从第gap个元素开始,依次与前面的元素比较,如果前面的元素较大,则将其后移gap个位置,直到找到合适的位置插入当前元素。
4、继续对每个子序列进行插入排序,直到所有子序列都排好序。
5、缩小gap的值为原来的一半,重复步骤2-4,直到gap为1时完成排序。
举例
假设有一个数组 [9, 5, 7, 1, 3],我们将使用希尔排序对其进行排序。首先,选择一个增量(gap),可以是数组长度的一半。在这个例子中,数组长度为5,所以我们选择增量为2。然后,我们将数组分为若干个子数组,每个子数组相隔增量个元素。对于这个例子,我们将数组分为两个子数组:[9, 7, 3] 和 [5, 1]。接下来,对每个子数组进行插入排序。在插入排序中,我们将每个元素与它前面的元素进行比较,并将它插入到正确的位置。对于这个例子,我们得到以下两个子数组:[3, 7, 9] 和 [1, 5]。然后,我们将增量减小一半,即变为1。此时,我们将整个数组作为一个子数组进行插入排序。对于这个例子,我们得到最终的排序结果:[1, 3, 5, 7, 9]。
复杂度分析
希尔排序是一种改进的插入排序算法,它通过将数组分成多个子序列进行排序,然后逐步缩小子序列的长度,最终使整个数组有序。希尔排序的时间复杂度取决于步长序列的选择。常用的步长序列有希尔增量序列和Hibbard增量序列。希尔增量序列是将数组长度不断除以2得到的序列,直到序列的最后一个元素为1。例如,对于一个长度为N的数组,希尔增量序列可以是N/2, N/4, N/8, ..., 1。Hibbard增量序列是将2^k - 1作为步长,其中k从1开始递增,直到2^k - 1大于等于数组长度N。例如,对于一个长度为N的数组,Hibbard增量序列可以是1, 3, 7, 15, ..., 2^k - 1。希尔排序的平均时间复杂度为O(n^1.3),其中n是数组的长度。这个时间复杂度是基于希尔增量序列的选择得出的。然而,希尔排序的时间复杂度并不是确定的,它可能会受到输入数据的影响。对于某些特定的输入数据,希尔排序的时间复杂度可能会更低,甚至接近O(n)。这是因为希尔排序在每一轮排序中,对于相隔较远的元素进行了交换,从而提前将较小或较大的元素移动到了正确的位置,减少了后续排序的次数。总结起来,希尔排序的时间复杂度是不确定的,但平均情况下为O(n^1.3)。
应用场景
数组规模较大:希尔排序在大规模数组排序时具有较好的性能表现,比如对百万级别的数据进行排序。数据分布较均匀:希尔排序对于数据分布较均匀的情况下,排序效率较高。如果数据分布不均匀,可能会导致排序效率下降。对稳定性没有要求:希尔排序是一种不稳定的排序算法,即相同元素的相对位置可能会发生变化。如果对排序结果的稳定性有要求,不适合使用希尔排序。对内存空间要求较低:希尔排序是一种原地排序算法,不需要额外的内存空间,适合在内存空间有限的情况下使用。
实际举例
排序算法:希尔排序可以用于对大规模数据进行排序,尤其是在数据量较大且无序程度较高的情况下,相比于其他排序算法,希尔排序具有较高的效率。数据库索引:在数据库中,索引是对表中的数据进行快速查找的一种数据结构。希尔排序可以用于对索引进行排序,提高数据库查询的效率。编程语言中的排序函数:许多编程语言中的排序函数底层实现使用了希尔排序算法,例如C++中的std::sort函数就是使用希尔排序作为默认实现。数据压缩:希尔排序可以用于对数据进行压缩,通过对数据进行排序,可以使得相同的数据连续出现,从而提高数据的压缩率。图像处理:希尔排序可以用于对图像进行排序,例如对像素点的颜色值进行排序,从而实现图像的特效处理。
代码实现
public class ShellSort {public static void shellSort(int[] arr) {int n = arr.length;for (int gap = n / 2; gap > 0; gap /= 2) {for (int i = gap; i < n; i++) {int temp = arr[i];int j = i;while (j >= gap && arr[j - gap] > temp) {arr[j] = arr[j - gap];j -= gap;}arr[j] = temp;}}}public static void main(String[] args) {int[] arr = {9, 5, 2, 7, 1, 8, 6, 3, 4};shellSort(arr);System.out.println("排序结果:");for (int num : arr) {System.out.print(num + " ");}}
}//排序结果:1 2 3 4 5 6 7 8 9
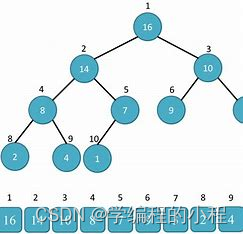
堆排序
堆排序是一种基于堆数据结构的排序算法,它的时间复杂度为O(nlogn)。堆排序的基本思想是将待排序的序列构建成一个大顶堆(或小顶堆),然后依次将堆顶元素与最后一个元素交换,再重新调整堆,重复这个过程直到整个序列有序。
步骤
堆排序是一种基于二叉堆的排序算法,1、构建最大堆(或最小堆):将待排序的数组看作是一个完全二叉树,根据堆的性质,可以通过从最后一个非叶子节点开始,依次向上调整每个节点,使得每个节点都满足堆的性质。这样就可以得到一个最大堆(或最小堆)。2、将堆顶元素与最后一个元素交换:将最大堆(或最小堆)的堆顶元素与数组的最后一个元素交换位置,这样最大(或最小)的元素就被放到了最后的位置。3、调整堆:将交换后的堆顶元素向下调整,使得堆的性质仍然成立。具体操作是将堆顶元素与其左右子节点中较大(或较小)的元素交换位置,然后继续向下调整交换后的节点,直到堆的性质满足。4、重复步骤2和步骤3直到完成排序:重复执行步骤2和步骤3,每次都将堆顶元素与当前未排序的部分的最后一个元素交换,并调整堆,直到所有元素都被交换到了正确的位置。这样就完成了堆排序。
举例
待排序序列:[4, 10, 3, 5, 1]建堆:从最后一个非叶子节点开始,依次向上调整,使得每个节点的值都大于等于其子节点的值。调整后的堆为:[10, 5, 3, 4, 1]排序:将堆顶元素10与最后一个元素1交换位置,并将堆的大小减1。交换后的堆为:[1, 5, 3, 4]。然后再对堆顶元素1进行一次向下调整,使得堆重新满足堆的定义。调整后的堆为:[5, 4, 3, 1]。再次排序:将堆顶元素5与最后一个元素1交换位置,并将堆的大小减1。交换后的堆为:[1, 4, 3]。然后再对堆顶元素1进行一次向下调整,使得堆重新满足堆的定义。调整后的堆为:[4, 1, 3]。再次排序:将堆顶元素4与最后一个元素3交换位置,并将堆的大小减1。交换后的堆为:[3, 1]。然后再对堆顶元素3进行一次向下调整,使得堆重新满足堆的定义。调整后的堆为:[1, 3]。最后排序:将堆顶元素1与最后一个元素3交换位置,并将堆的大小减1。交换后的堆为:[3]。堆的大小为1,排序完成。
最终排序结果:[1, 3, 4, 5, 10]
复杂度分析
建堆:建堆的时间复杂度为O(n),其中n为待排序序列的长度。调整堆:调整堆的时间复杂度为O(logn)。在堆排序过程中,需要调整堆的次数为n-1次,每次调整堆的时间复杂度为O(logn)。堆排序:堆排序的时间复杂度为O(nlogn)。在堆排序过程中,需要进行n-1次调整堆的操作,每次调整堆的时间复杂度为O(logn)。因此,堆排序的总时间复杂度为O(nlogn)。综上所述,堆排序的时间复杂度为O(nlogn)。
应用场景
需要对大量数据进行排序的场景,堆排序的时间复杂度为O(nlogn),效率较高。需要稳定性较差的排序算法,堆排序是一种不稳定的排序算法,适用于不要求相同元素的相对位置保持不变的场景。需要对数据进行动态排序的场景,堆排序可以在不断插入新元素的情况下,快速对数据进行排序。需要找出最大或最小的前k个元素的场景,堆排序可以通过构建最大堆或最小堆,快速找到最大或最小的元素。
实际举例
优先级队列:堆排序可以用于实现优先级队列,其中每个元素都有一个优先级。通过使用最大堆,可以确保优先级最高的元素始终位于堆的根节点,从而可以快速找到并删除具有最高优先级的元素。任务调度:在任务调度中,每个任务都有一个优先级和执行时间。通过使用最小堆,可以按照任务的优先级和执行时间对任务进行排序,从而实现高效的任务调度。多路归并排序:堆排序可以用于多路归并排序,其中有多个有序序列需要合并成一个有序序列。通过使用最小堆,可以选择每个有序序列的最小元素进行合并,从而实现高效的多路归并排序。求Top K问题:在一组数据中,找到最大或最小的K个元素。通过使用最大堆,可以维护一个大小为K的堆,每次从数据中取出一个元素与堆顶元素比较,如果比堆顶元素大,则替换堆顶元素并重新调整堆,最终堆中的元素就是最大的K个元素。中位数问题:在一组数据中,找到中间位置的元素。通过使用最大堆和最小堆,可以将数据分为两部分,其中最大堆存储较小的一半数据,最小堆存储较大的一半数据。这样可以快速找到中位数,并支持动态添加和删除元素。代码实现
public class HeapSort {public void heapSort(int[] arr) {int n = arr.length;// 建立最大堆for (int i = n / 2 - 1; i >= 0; i--)heapify(arr, n, i);// 逐个将堆顶元素移到数组末尾for (int i = n - 1; i >= 0; i--) {// 将当前堆顶元素(最大值)与数组末尾元素交换int temp = arr[0];arr[0] = arr[i];arr[i] = temp;// 重新调整堆,找出剩下元素的最大值heapify(arr, i, 0);}}// 调整堆void heapify(int[] arr, int n, int i) {int largest = i; // 初始化最大值为根节点int left = 2 * i + 1; // 左子节点int right = 2 * i + 2; // 右子节点// 如果左子节点大于根节点,将最大值设为左子节点if (left < n && arr[left] > arr[largest])largest = left;// 如果右子节点大于当前最大值,将最大值设为右子节点if (right < n && arr[right] > arr[largest])largest = right;// 如果最大值不是根节点,交换根节点与最大值,并继续调整堆if (largest != i) {int swap = arr[i];arr[i] = arr[largest];arr[largest] = swap;heapify(arr, n, largest);}}// 测试代码public static void main(String[] args) {int[] arr = {9, 5, 2, 7, 1, 8, 3};HeapSort heapSort = new HeapSort();heapSort.heapSort(arr);System.out.println("排序结果:");for (int num : arr) {System.out.print(num + " ");}}
}
//输出结果为:1 2 3 5 7 8 9。