作者：CSDN @ _养乐多_

本文将介绍Vision Transformers （ViT）中的关键点。包括图像分块（Image Patching）、图像块嵌入（Patch Embedding）、类别标记、（class_token）、QKV矩阵计算过程、余弦相似度（cosine similarity）、Softmax、自注意力机制等概念。主要介绍QKV矩阵计算过程。

---

---

一、Image Patching

图像被分成小的块的过程是 “Image Patching”（图像分块）或者简称 “Patching”。在这个过程中，图像被划分成一系列大小相同或不同的小块，这些小块通常被称为 “Image Patches”（图像块）或简称 “Patches”。

图像分块（Image Patching）过程如图所示，

“Patch” 是指图像中的一个小块区域或片段。这个概念通常用于将大尺寸的图像分解成更小的部分，以便对每个小块进行单独处理、分析或特征提取。

将图像分成小块（即 Patch）可以带来的优势：

• 特征提取：在一些任务中，特定区域的信息比整个图像更有用。通过对每个 Patch 进行特征提取，可以获得更细粒度的信息，有助于更好地理解图像内容。

• 处理大尺寸图像：对于非常大的图像，可能会遇到计算和存储方面的限制。将图像分成小的 Patch 可以帮助降低计算复杂度，并且可以更轻松地处理这些小尺寸的块。

• 自适应性：在一些自适应处理的算法中，对于不同的图像区域采取不同的策略是很常见的。将图像划分成 Patch 可以使算法在局部区域上更加灵活和自适应。

二、Patch Embedding

“Patch Embedding” 是一个计算机视觉领域的概念，它与图像处理和深度学习中的卷积神经网络（Convolutional Neural Networks，CNN）相关。

传统的卷积神经网络在图像处理时使用的是像素级的操作，通过卷积核在图像上滑动进行特征提取。而在"Patch Embedding"中，这个概念引入了更高级的特征表示方式。它将输入的图像分成小的块（也称为“patch”），然后将每个小块转换为低维的向量表示。这种向量表示可以被用作后续任务的输入。

Patch Embedding的目的在于降低计算复杂度并提高特征提取的效率。由于在传统的卷积操作中，相邻的像素通常会有大量重叠，而Patch Embedding将图像分成块后，可以减少冗余计算，同时保留了重要的特征信息。

三、Class token

“Class token” 是一个特殊的令牌，用于表示整个图像的类别信息。通常，它会被添加到 Patch Embedding 后得到的向量序列中的某个位置，使得模型能够利用这个类别信息进行分类或生成任务。

3.1 Add Class token

在Transformer模型中，“Class token” 通常被添加在输入序列的开头，并且在训练过程中会经过特定的注意力机制，以使得模型能够对类别信息进行编码和利用。

在 Patch Embedding 操作之后，“Class token” 被添加到 Patch Embedding 向量序列的开头，用于表示整个图像的类别信息，以辅助后续的图像分类或生成任务。

下面举例说明Class token，假设此次应用是为了分类图像是不是石原里美。我们使用 one-hot 编码的方式表示类别信息。那么类别信息就有两种，是和不是，现在用向量 [1, 0] 表示是，[0, 1] 表示不是。那么class_token就是 [1, 0] 或者 [0, 1] 。

现在，我们将这个 “Class token” 与每个小块的 Patch Embedding 向量连接在一起，得到最终的输入序列。假设得到的 196 个 Patch Embedding 向量分别为：

[v1, v2, v3, ..., v196]

那么，添加 “Class token” 后的最终输入序列为：

[Class_token, v1, v2, v3, ..., v196]

这样，整个输入序列中的第一个向量就是 “Class token”，它包含了整个图像的类别信息，即图像属于是不是石原里美。模型在训练过程中可以利用这个类别信息，帮助进行图像分类任务。

往细一点讲，假设 v1 是一个 2 维向量，表示为：

v1 = [0.2, 0.7]

这个向量表示第一个小块的特征。现在，我们将 “Class token” 和 v1 连接在一起，得到最终的输入序列：

[Class_token, v1]

假设 “Class token” 表示图像属于石原里美的类别，它的 one-hot 编码为：

[1, 0]

那么最终的输入序列是：

[[1, 0], [0.2, 0.7]]

这个输入序列包含了整个图像的类别信息（属于石原里美的概率为 1，不是石原里美的概率为 0）以及第一个小块的特征向量 [0.2, 0.7]。

3.2 Positional Encoding

在了解了class token 以后，我们来看看 vit 中的 class token 。

在 Vision Transformer (ViT) 模型中，“PE” 表示位置编码（Positional Encoding），用于将图像中的每个 Patch Embedding 向量与其位置信息相关联，用于将整个图像的全局位置信息引入到 Transformer 模型中。

位置编码是为了给 Transformer 模型提供输入序列中的位置信息，因为 Transformer 模型没有像卷积神经网络那样显式地保留位置信息。在自然语言处理任务中，输入是一个词语序列，为了保留词语的位置信息，通常会添加位置编码。类似地，在 ViT 中，输入是图像的 Patch Embedding 序列，为了保留 Patch 的位置信息，也需要添加位置编码。

在 ViT 中，PE(pos, 2i) 和 PE(pos, 2i + 1) 是用来计算 “Class token” 的位置编码公式。位置编码使用的是 sin 和 cos 函数来计算。对于 “Class token” 的位置编码，计算方式为：

$$PE(pos,2i)=sin(pos/10000^{2i/dmodel})$$
$$PE(pos,2i+1)=cos(pos/10000^{2i/dmodel})$$

位置编码采用了正弦和余弦函数的形式，其中 PE(pos, 2i) 是对应维度为偶数的位置编码，PE(pos, 2i + 1) 是对应维度为奇数的位置编码。在计算时，pos 表示 Patch 在序列中的位置，i 是位置编码的维度索引，从 0 开始，dmodel 是 Transformer 模型中的隐藏层维度（也称为特征维度）。

这种位置编码的计算方式在 Transformer 中是常见的，它使得不同位置的 Patch Embedding 向量在特征空间上具有不同的位置偏移，以便于模型在处理序列数据时考虑到它们的相对位置关系。

---

为了更好地说明位置编码的计算过程，我们来举一个简化的例子。假设我们有一个图像，将其分成 4x4 个小块（Patch），共计 16 个小块，每个小块用一个 2 维向量表示。我们假设隐藏层大小（d_model）为 4。

现在，我们来计算 “Class token” 和每个小块的位置编码。

首先，“Class token” 的位置为整个图像，我们可以选择一个虚拟的位置编号 pos = 0 来表示 “Class token” 的位置。然后，我们计算 “Class token” 的位置编码：

d_model = 4
i = 0PE(pos=0, 2i) = sin(0 / 10000^(2*0 / 4)) = sin(0) = 0
PE(pos=0, 2i + 1) = cos(0 / 10000^(2*0 / 4)) = cos(0) = 1

所以 “Class token” 的位置编码为 [0, 1]。

接下来，我们计算每个小块的位置编码。假设小块的位置编号从 1 到 16。我们可以使用以下公式来计算每个小块的位置编码：

d_model = 4
i = 0, 1, 2, 3pos = 1
PE(pos=1, 2*0) = sin(1 / 10000^(2*0 / 4)) = sin(1) ≈ 0.8415
PE(pos=1, 2*0 + 1) = cos(1 / 10000^(2*0 / 4)) = cos(1) ≈ 0.5403pos = 2
PE(pos=2, 2*0) = sin(2 / 10000^(2*0 / 4)) = sin(2) ≈ 0.9093
PE(pos=2, 2*0 + 1) = cos(2 / 10000^(2*0 / 4)) = cos(2) ≈ -0.4161

…
依此类推，计算每个小块的位置编码。最终得到每个小块的位置编码的结果。

请注意，这只是一个简化的例子，并且隐藏层大小（d_model）和小块的位置编号可能会根据实际情况有所不同。实际中，ViT 模型使用更高维度的隐藏层，并且位置编号会更加复杂。这里的目的是为了演示位置编码的计算过程。

四、QKV

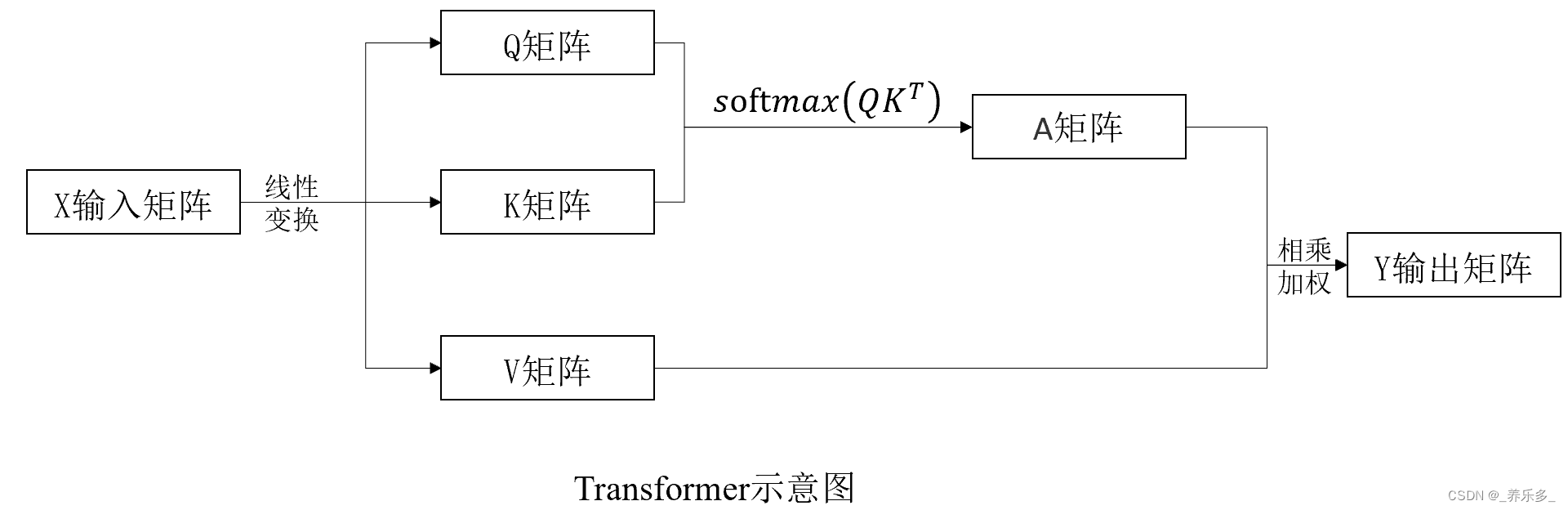
如上图所示，QKV 矩阵是在自注意力机制（Self-Attention Mechanism）中用于计算注意力权重的三个矩阵。这三个矩阵通常是通过对输入序列进行线性变换得到的。它们分别是：

• Q矩阵（Query Matrix）：Q矩阵用于生成查询向量，每个查询向量代表一个小块（Patch）在注意力机制中的查询，即用于寻找与当前小块相关的信息。

• K矩阵（Key Matrix）：K矩阵用于生成键向量，每个键向量代表一个小块（Patch）在注意力机制中的键，即用于表示当前小块与其他小块之间的关系。

• V矩阵（Value Matrix）：V矩阵用于生成值向量，每个值向量代表一个小块（Patch）在注意力机制中的值，即用于表示当前小块的特征信息。

首先需要知道的是X矩阵和Y矩阵的维度大小是一样的，输入维度和输入维度一样。

具体来说，在自注意力机制中，输入序列首先通过三个不同的线性变换，分别得到查询矩阵 Q、键矩阵 K 和值矩阵 V。 这三个矩阵将用于计算注意力权重，从而对输入序列进行加权求和，得到最终的表示。

其中，Q和K的点乘得到的矩阵就是注意力权重矩阵A。假设如果只有V矩阵，不经过Q和K的过程，那么这就算是普通的网络，没有加入注意力机制。

假设不管你用什么线性变换方法，也不过你线性变换用了多少隐藏层（这部分自行百度），现在我们得到了QKV矩阵，并且添加了 class token。如下图所示，

当然我们计算的时候，QKV都是被拉伸成了一行，为了方便表示，这里画的还是矩形形式。

4.1 cosine similarity

在了解Q和K点乘之前，需要理解余弦相似度的概念。因为Q和K的点乘就是在比较其余弦相似度大小，如果Q中第一个patch和K中所有patch相比较，进行点乘，那么他们的余弦相似度会被计算。

余弦相似度越大，自注意力权重越大。

下面是余弦相似度的概念和计算方式，

余弦相似度是一种用于衡量两个向量之间相似性的度量方法，常用于计算两个向量的方向是否相似。在余弦相似度中，向量的长度并不影响相似度的计算，因此它更关注向量的方向。

假设有两个向量 A 和 B，它们可以表示为：

$$A=[a_1,a_2,a_3,...,a_n]$$
$$B=[b_1,b_2,b_3,...,b_n]$$

其中 a₁、a₂、…、aₙ 和 b₁、b₂、…、bₙ 分别是两个向量的元素。

余弦相似度的计算公式如下：

$$cosine\_similarity=(A\cdot B)/(||A||\ast ||B||)$$

其中，

• A·B 表示向量 A 和向量 B 的点积（内积），即 a₁ * b₁ + a₂ * b₂ + … + aₙ * bₙ。
• ||A|| 表示向量 A 的范数（或长度），即 √(a₁² + a₂² + … + aₙ²)。
• ||B|| 表示向量 B 的范数，即 √(b₁² + b₂² + … + bₙ²)。

计算余弦相似度时，首先计算向量 A 和向量 B 的点积，然后分别计算它们的范数。最后将点积除以两个向量的范数的乘积，得到余弦相似度值。余弦相似度的取值范围在 -1 到 1 之间，

• 当余弦相似度为 1 时，表示两个向量的方向完全相同，即它们在空间中指向相同的方向。
• 当余弦相似度为 -1 时，表示两个向量的方向完全相反，即它们在空间中指向相反的方向。
• 当余弦相似度为 0 时，表示两个向量的方向垂直，即它们在空间中互相垂直。

4.2 Q @ $K^T$

下面我们来看一看 Q 和 K 计算权重矩阵A的过程，如图红框中的过程，

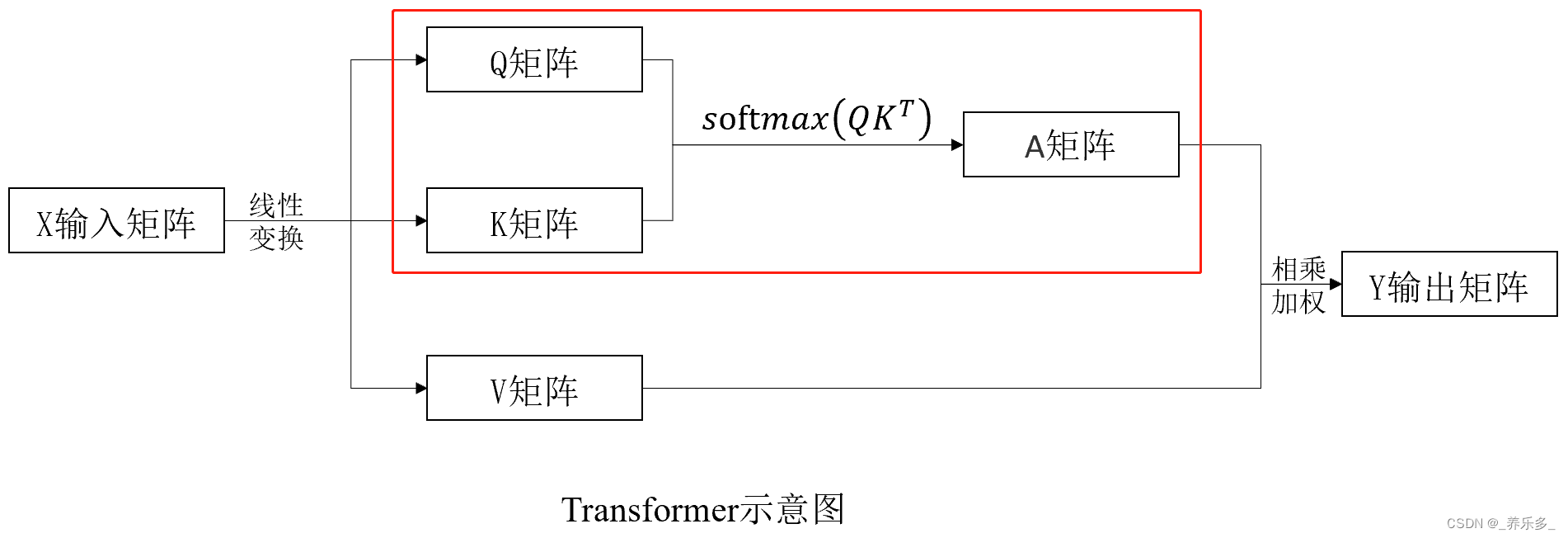
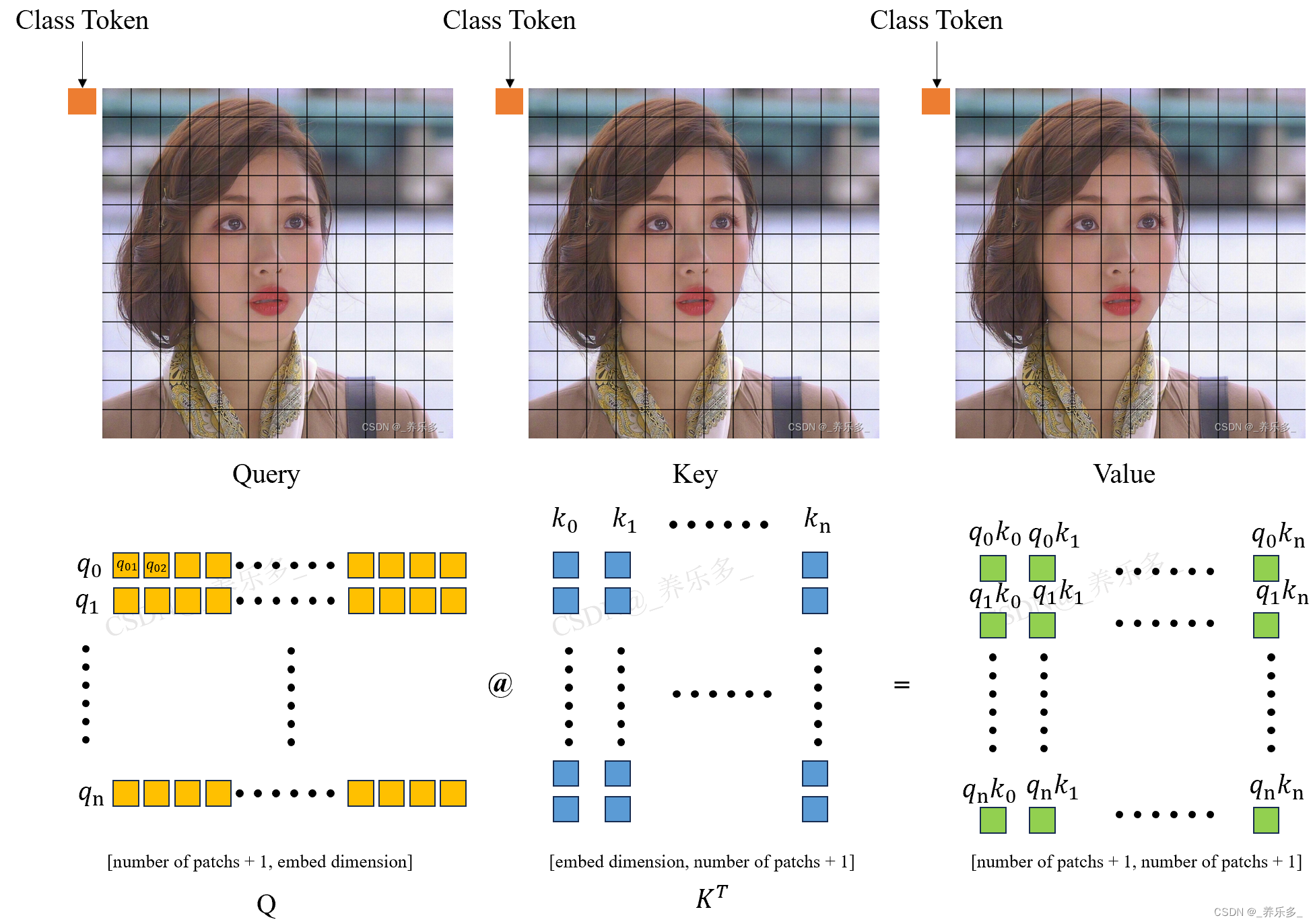
如上图所示，假设黄色矩形表示Q矩阵中的元素，蓝色矩形表示$K^T$矩阵中的元素，绿色矩形表示Q点乘K之后的结果矩阵中的元素。其中，q₀表示一行，k₀表示一列，q₀k₀表示黄色的一行和蓝色的一列点乘得到的一个数。

这里的 q₀ 就是 class_token 拉成一维的向量，q₁ 就是 Q 矩阵（石原里美图片）第一个 patch 向量；k₀就是 K 矩阵转置后的矩阵的一列，表示的是 class_token 拉成一维的向量，k₁是 K 矩阵（石原里美图片）第一个 patch 向量。

4.3 softmax( (Q @ $K^T$) / $\sqrt{dk}$ )

首先，让给我们了解一下 Softmax 函数。Softmax 是一种用于将向量元素转换为概率分布的函数。给定一个输入向量 z = [z₁, z₂, …, zₙ]，Softmax 函数将每个元素 zᵢ 转换为一个概率值 pᵢ，使得所有概率值的和等于 1。

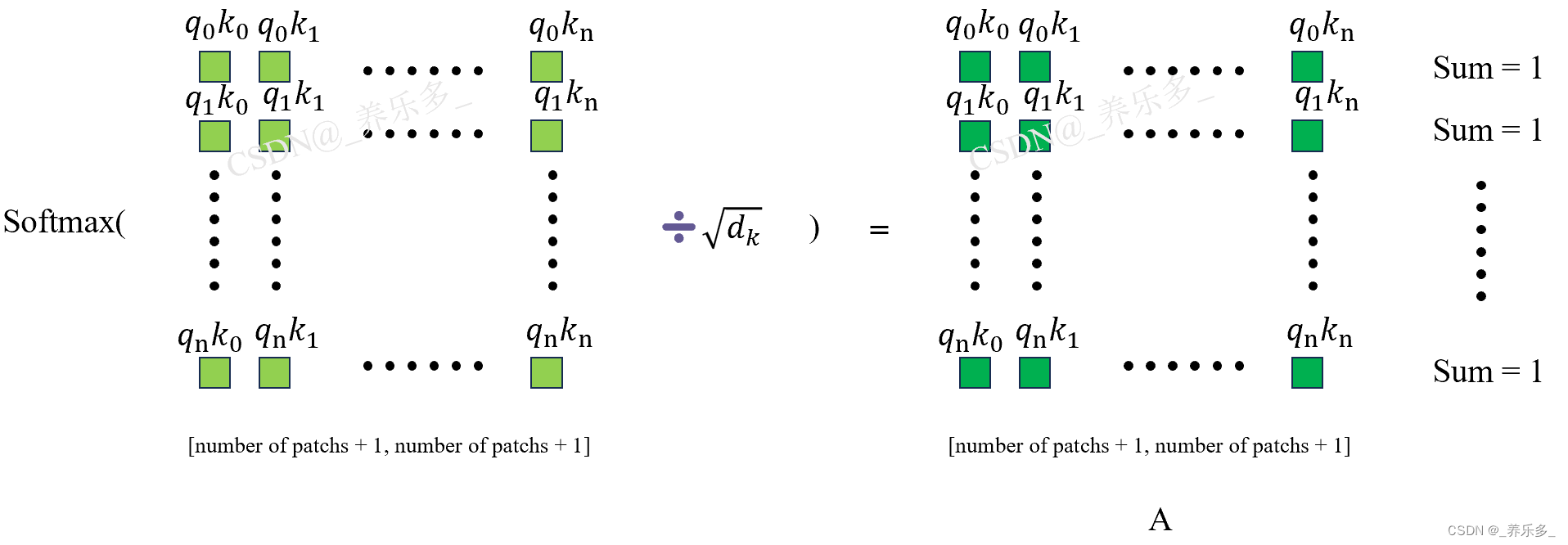
举个例子，这里将q₀k₀、q₀k₁…q₀k_n的值转变为概率值，并将他们的和变为1。

在自注意力机制中，除以 $\sqrt{d_k}$ 是为了缩放注意力权重，从而避免在深度较大的 Transformer 模型中由于注意力权重过大造成的梯度爆炸问题。

这里的 d_k 是模型中注意力头（attention head）的维度（dimension），那么点积结果的大小为 d_k ，而不同位置之间的点积结果的值范围可能差异较大。如果不进行缩放，一些较大的点积值在经过 Softmax 后可能会变得非常大，而较小的点积值在经过 Softmax 后可能接近于0。这会导致注意力权重的巨大差异，使得一些位置对其他位置的影响过大或过小，从而影响模型的学习和泛化能力。

通过除以 $\sqrt{d_k}$，可以将点积结果进行缩放，使得所有点积结果的范围相对稳定，不会出现过大或过小的情况。这样，Softmax 后得到的注意力权重就会相对均衡，并且更有利于模型学习有效的全局关系和表示。

4.4 A @ V

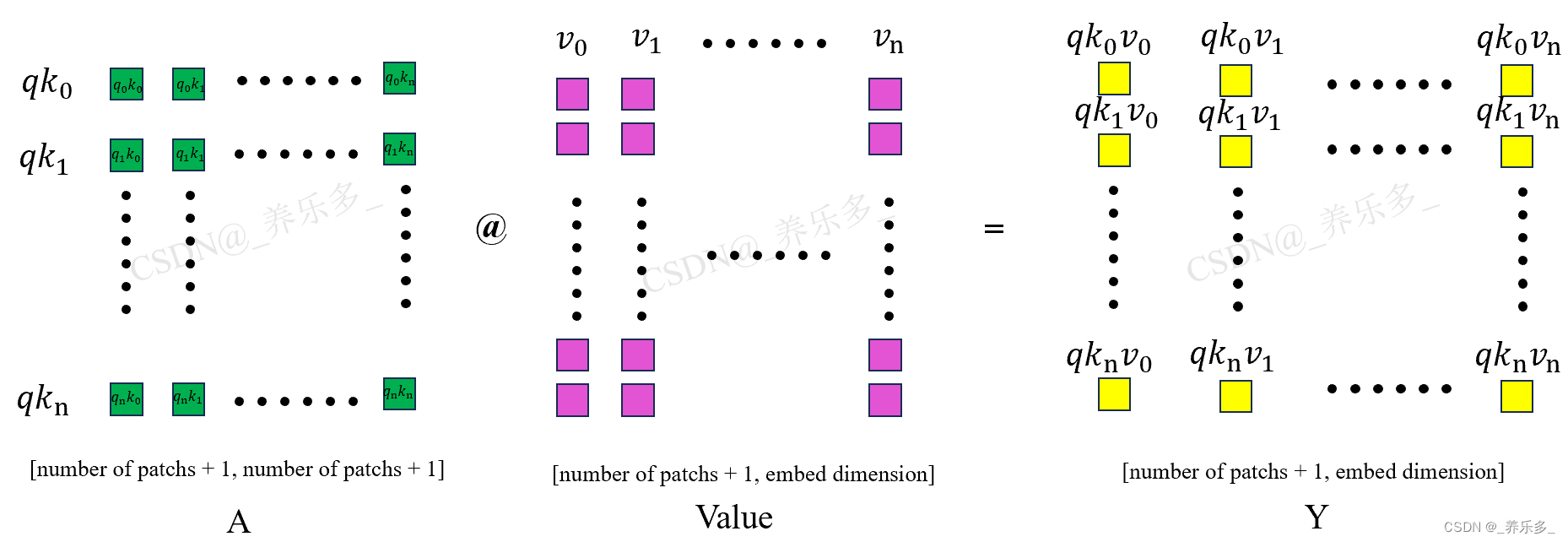
如图所示，经过之前的计算，我们已经得到了权重 A 矩阵，将 A 和 Value 矩阵点乘，就是将注意力权重矩阵应用到 V 矩阵上了。图中黄色的矩形就是经过注意力机制计算得到的 Y 矩阵。Y 矩阵的维度和X 输入矩阵的维度是一模一样的。所以说 Transform 是一个即插即用的模块。

这里的qk₀是 A 权重矩阵的一行，v₀是 Value 矩阵的一列，qk₀v₀是它们点乘以后得到的一个数（即q₀k₀v₀₀+q₀k₁v₁₀+q₀k₂v₂₀+…）。

声明：
本人作为一名作者，非常重视自己的作品和知识产权。在此声明，本人的所有原创文章均受版权法保护，未经本人授权，任何人不得擅自公开发布。
本人的文章已经在一些知名平台进行了付费发布，希望各位读者能够尊重知识产权，不要进行侵权行为。任何未经本人授权而将付费文章免费或者付费（包含商用）发布在互联网上的行为，都将视为侵犯本人的版权，本人保留追究法律责任的权利。
谢谢各位读者对本人文章的关注和支持！