Android多语言开发自动化生成工具

        在做 Android 开发的过程中，经常会遇到多语言开发的场景，尤其在车载项目中，多语言开发更为常见。对应多语言开发，通常都是在中文版本的基础上开发其他国家语言，这里我们会拿到中-外语言对照表，这里的工作难度其实并不高，但是工作量却是非常的大，而且都是复制/粘贴的无聊操作，如何能快速的完成这种简单重复的操作呢？这里我们就来简单实现一下。

一、准备工作

1、多语言需求

        假如我们需要中文、英文和俄文三种语言的开发，同时我们拿到了多语言的翻译表格：

模块namezhenru
SystemUIcancel取消Cancelотмен
save保存Saveсохран
file_name文件名称File NameИмя файла
Launchersave_path保存路径Saved ToПуть сохранения.
text_error_tip字数超过限制The number of words exceeds the limit.Число слов превышает предел

        可以看到，对于车载开发来说，多语言开发肯定是所以应用都需要修改的，这里以 SystemUI 和 Launcher 为例。其中 name 表示在 strings.xml 中的 name 字段，zh、en 和 ru 分别表示中文、英文和俄文的简写。

2、制作xls表格

        这里我们用的是 xls（暂时只支持 xls 格式的表格解析）的表格来罗列国际化的语言字段，形如下表这样的 translation.xls。

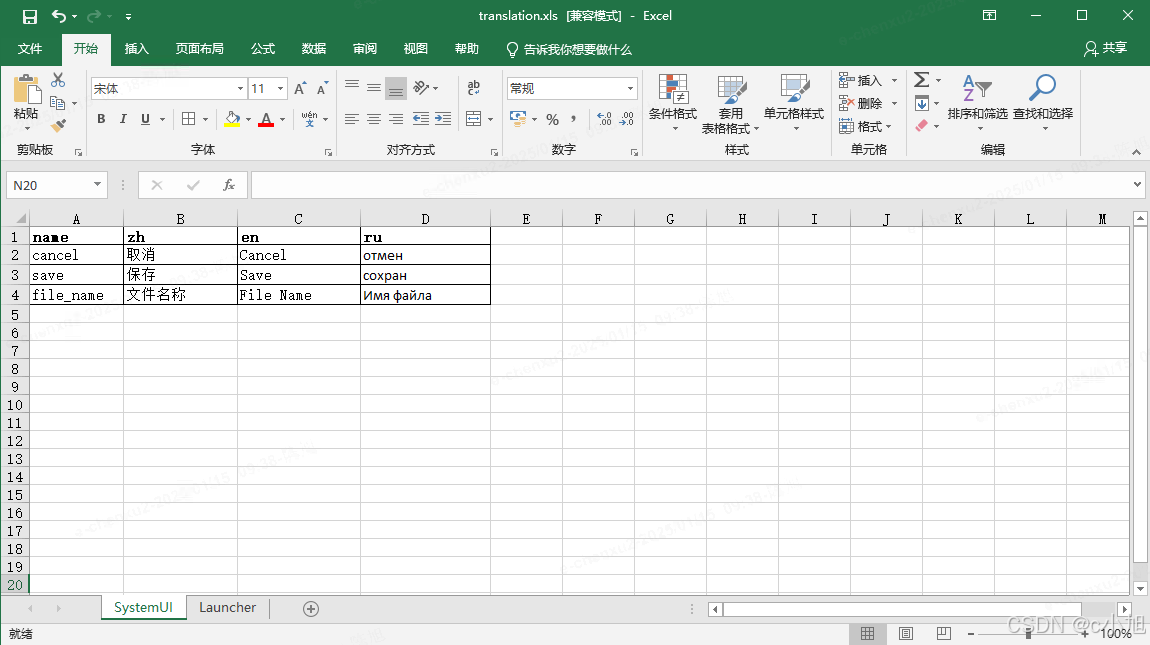
        这里使用两个 Sheet 分别存在 SystemUI 和 Launcher 多语言数据，多模块继续增加 Sheet 即可（这里的 Sheet 其实就是 string.mxl 的数量）。再看一下 Launcher 的表格数据：

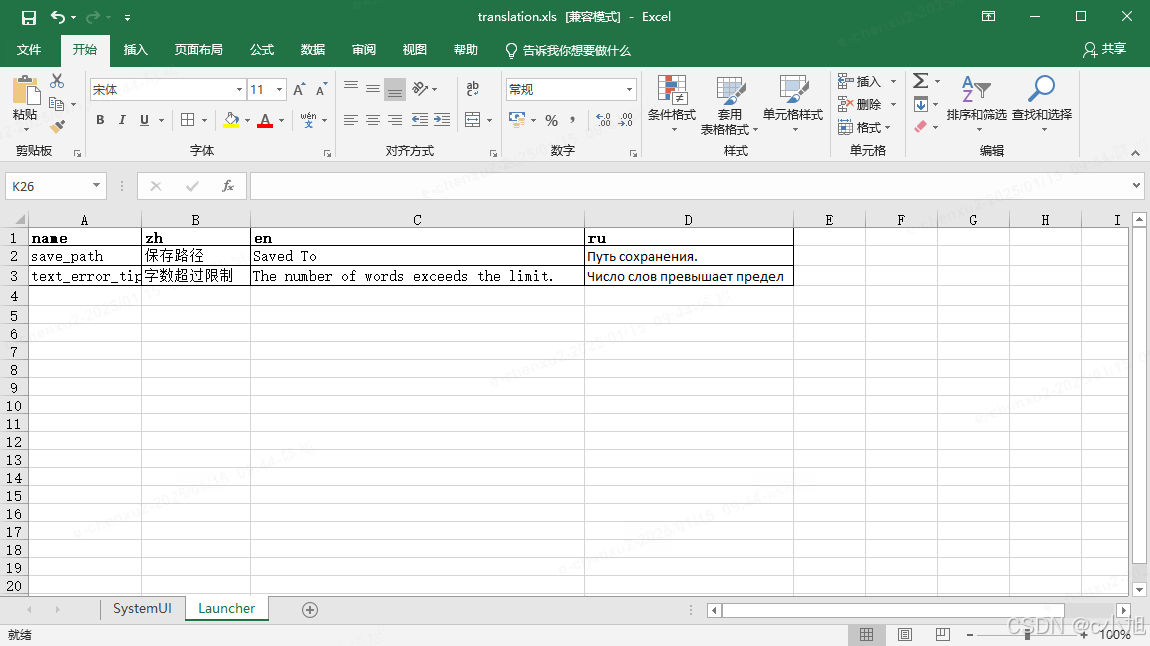
表格转化 

        在实际的操作中，我们创建的表格都是 xlsx 格式的表格文件，直接转换一下即可，操作如下：

1）点击表格左上角的文件。

2）这里选择另存为或导出都可以。

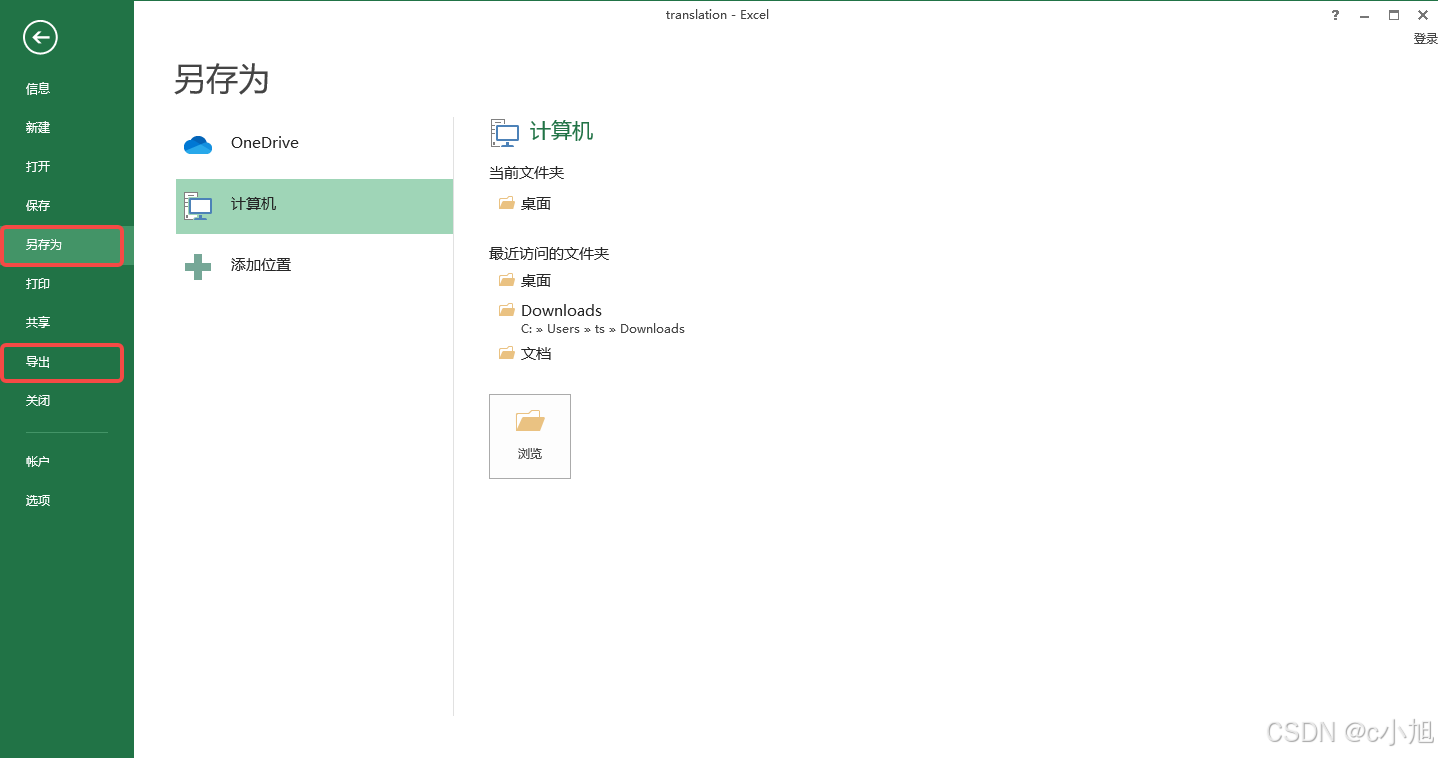
3）另存为在保存文件是将格式修改为 Excel 97-2003 工作簿即可。

        同样选择导出时也是同样的选择：

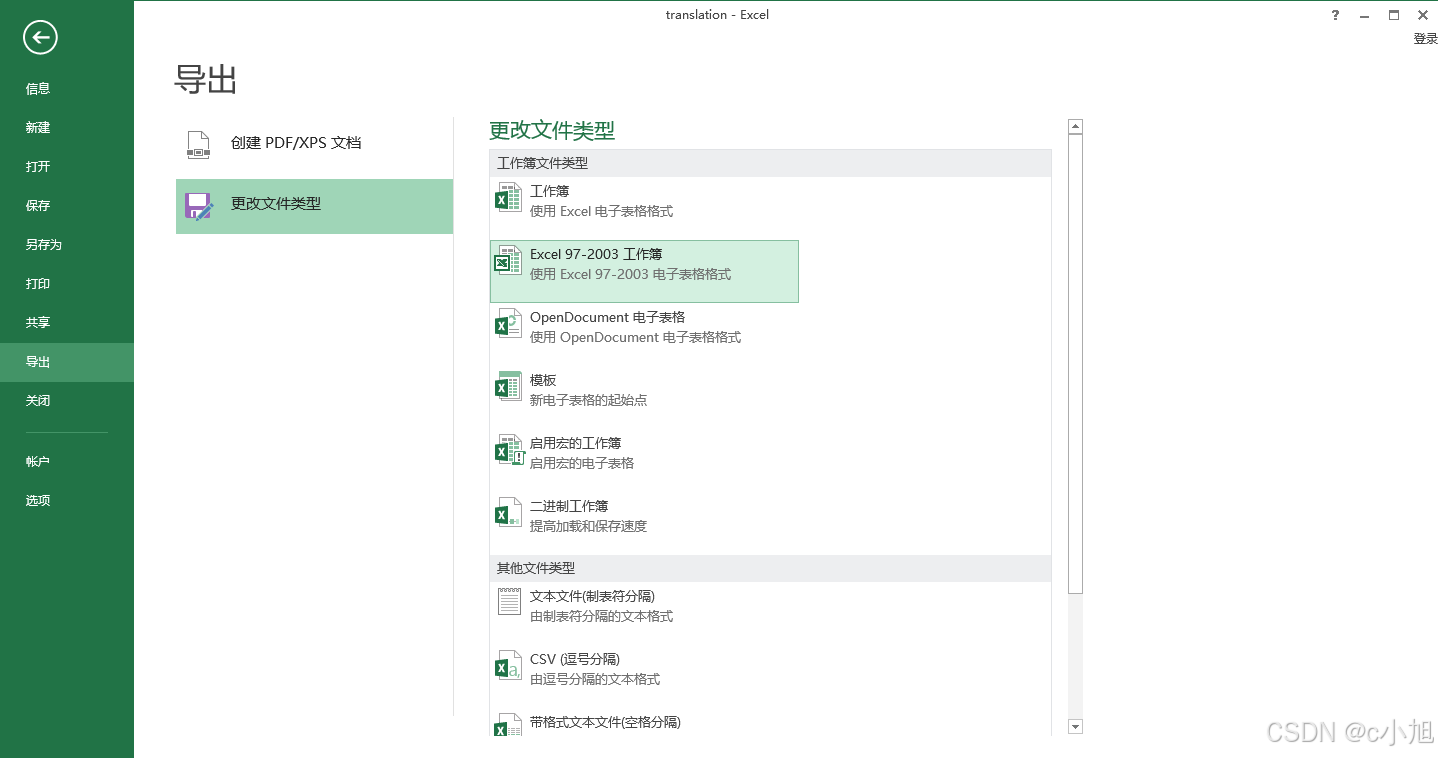
二、功能实现

        这里我们选择使用 Android 项目来实现多语言 strings.xml 的自动化生成工作，所以先创建一个 Android 项目，然后按照下面的步骤一步一步实现即可。

1、依赖引用

        我们是基于 jxl 进行，所以还需要依赖一个 jxl。

dependencies{implementation 'net.sourceforge.jexcelapi:jxl:2.6.12'
}

2、解析工具类

        实现 xls 文件解析及生成 strings.xml 的工具类。

import org.jxls.reader.XLSReader;
import jxl.Workbook;
import jxl.Sheet;
import jxl.Cell;
import java.io.File;
import java.io.FileWriter;
import java.io.BufferedWriter;
import java.util.HashMap;
import java.util.ArrayList;
import java.util.Map;public class TranslationHandler {private static final HashMap<Integer, String> codeMap = new HashMap<>();private static final HashMap<String, ArrayList<TranslationBean>> keyAndValueMap = new HashMap<>();private static final String DIR = "/storage/emulated/0/Download/";private static final String XLS_PATH = DIR + "translation.xls";private static final File xlsFile = new File(XLS_PATH);private static final WorkbookSettings workbookSettings = new WorkbookSettings();static {if (!codeMap.isEmpty()) codeMap.clear();if (!keyAndValueMap.isEmpty()) keyAndValueMap.clear();// 设置编码防止其他国字乱码workbookSettings.setEncoding("ISO-8859-1");}// 开始入口函数public static void startAnalyze(){int sheetNums = 0;try{sheetNums = Workbook.getWorkbook(xlsFile, worlkbookSettings).getNumberOfSheets();for (int sheetNum = 0; sheetNum < sheetNums; sheetNUm++)// 第2列(column=B)开始国际化,一共有3列是需要国网示化handleXlsExcel(sheetNum, startColumn: 1, 3);}} catch (Exception e){e.printStackTrace();}/*** @param sheetNum: 表示sheet页数量（0表示第1张sheet）* @param startColumn: 从0开始，第几列开始是国际化* @param columnCount: 一共有多少列是国际化*/private static void handleXlsExcel(int sheetNum, int startColumn, int columnCount) throws Exception {// workbook 与 sheet 是一对一Workbook workbook = Workbook.getWorkbook(xlsFile, workbookSettings);Sheet sheet = workbook.getSheet(sheetNum);System.out.println("sheet0 = " + sheet.getName());// 表示从第1行开始读取for (int row = 0; row < sheet.getRows(); row++) {if (row == 0) {for (int column = 0; column < columnCount; column++) {int columnIndex = startColumn + column;// B1, C1, D1单元格的内容表示国家代码String code = sheet.getCell(columnIndex, row).getContents();codeMap.put(columnIndex, code);keyAndValueMap.put(code, new ArrayList<>());}} else {// A1 ~ A[num] 单元格String key = sheet.getCell(0, row).getContents();if (key == null || "".equals(key)) break;for (int column = 0; column < columnCount; column++) {int columnIndex = startColumn + column;String code = codeMap.getOrDefault(columnIndex, "null");TranslationBean bean = new TranslationBean(key,sheet.getCell(columnIndex, row).getContents());ArrayList<TranslationBean> translationList = keyAndValueMap.get(code);if (translationList != null) {translationList.add(bean);}}}}workbook.close();File dir = new File(DIR, sheet.getName());if (!dir.exists()) dir.mkdir();// 使用 try-with-resources 确保文件流正确关闭for (String code : keyAndValueMap.keySet()) {File defaultDir = new File(dir, "values-" + code);if (!defaultDir.exists() && !defaultDir.mkdirs()) {System.err.println("Failed to create directory: " + defaultDir.getAbsolutePath());continue;}File file = new File(defaultDir, "strings.xml");try {if (!file.exists() && !file.createNewFile()) {System.err.println("Failed to create file: " + file.getAbsolutePath());continue;}System.out.println("Creating or updating file at: " + file.getAbsolutePath());try (BufferedWriter bw = new BufferedWriter(new FileWriter(file))) {bw.write("<resources>");bw.newLine();for (TranslationBean value : keyAndValueMap.get(code)) {bw.write("\t<string name=\"" + escapeXml(value.getKey()) + "\">" + escapeXml(value.getValue()) + "</string>");bw.newLine();}bw.write("</resources>");}System.out.println("成功生成文件: " + file.getAbsolutePath());} catch (Exception e) {e.printStackTrace();System.err.println("Error writing to file: " + file.getAbsolutePath());}}}private static String escapeXml(String input) {return input.replace("&", "&amp;").replace("<", "&lt;").replace(">", "&gt;").replace("\"", "&quot;").replace("'", "&apos;");}static class TranslationBean {private final String key;private final String value;public TranslationBean(String key, String value) {this.key = key;this.value = value;}public String getKey() {return key;}public String getValue() {return value;}}
}

        这里只需要调用 startAnalyze() 方法就可以开始自动化生成多语言 strings.xml 文件，但是需要有一个前提，那就是在对应目录中放置上面的 .xls 文件，这里我们放置在 /storage/emulated/0/Download/ 下，文件名为 translation.xls。

2、开始接口调用

        如果是调用开始接口是很简单的，在我们的 Activity 中直接调用或者增加一个按钮再点击事件中调用 TranslationTools.startAnalyze() 方法即可。但是在 Android 文件读写是需要相关权限的，这里我就直接上代码了，对于代码的理解部分可以参考《Android 开发中的权限申请》。

添加静态权限

<uses-permission android:name="android.permission.WRITE_EXTERNAL_STORAGE" />
<uses-permission android:name="android.permission.READ_EXTERNAL_STORAGE" />
<uses-permission android:name="android.permission.MANAGE_EXTERNAL_STORAGE"tools:ignore="ScopedStorage" />

增加动态权限

if(Build.VERSION.SDK_INT>=Build.VERSION_CODES.M&& context.checkSelfPermission(Manifest.permission.READ_EXTERNAL_STORAGE)!= PackageManager.PERMISSION_GRANTED) {//请求权限((Activity)context).requestPermissions(new String[]{Manifest.permission.READ_EXTERNAL_STORAGE,Manifest.permission.WRITE_EXTERNAL_STORAGE},1);
}

外部权限设置

public static boolean checkStorageManagerPermission(Context context) {if (Build.VERSION.SDK_INT >= Build.VERSION_CODES.R && !Environment.isExternalStorageManager()) {Intent intent = new Intent(Settings.ACTION_MANAGE_ALL_FILES_ACCESS_PERMISSION);context.startActivity(intent);return false;}return true;
}

        在拿到所有权限后就可以调用上面的 startAnalyze() 开始接口了。

三、文件生成/导出

1、文件生成

        在执行上面的 startAnalyze() 方法后，会在同目录 /storage/emulated/0/Download/ 下生成如下结构的文件：

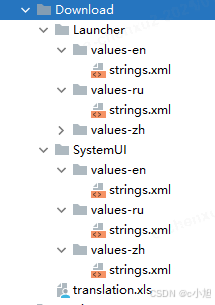
        这里 translation.xls 是我们最开始保存的 .xls 文件，而 SystemUI 和 Launcher 文件夹及下面的文件则是我们执行完代码自动生成的。下面我们简单看一下其中的文件。

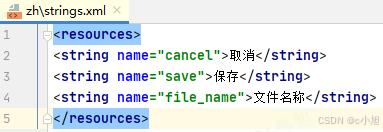
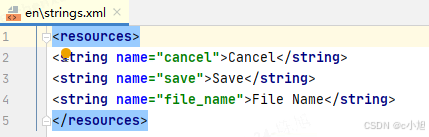
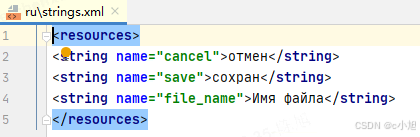
         可以看到这里的 SystemUI 对应的多语言 strings.xml 文件都是与上面的 .xls 表格对应的。

2、文件导出

1）在 Studio 中选择 View > Tool Windows > Device File Explorer，就会显示虚拟机的存储信息。

2）在虚拟机的存储设备中，找到 mnt > sdcard > Download，就会看到上面生成文件列表。

3）选择对应文件保存到制定路径即可。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.rhkb.cn/news/7502.html

如若内容造成侵权/违法违规/事实不符，请联系长河编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

数据结构——堆（C语言）

数据结构——堆（C语言）

基本概念&#xff1a; 1、完全二叉树&#xff1a;若二叉树的深度为h&#xff0c;则除第h层外&#xff0c;其他层的结点全部达到最大值&#xff0c;且第h层的所有结点都集中在左子树。 2、满二叉树&#xff1a;满二叉树是一种特殊的的完全二叉树&#xff0c;所有层的结点都是最…
阅读更多...
const的用法

const的用法

文章目录 一、C和C中const修饰变量的区别二、const和一级指针的结合const修饰的量常出现的错误是:const和一级指针的结合总结&#xff1a;const和指针的类型转换公式 三、const和二级指针的结合 一、C和C中const修饰变量的区别 C中&#xff1a;const必须初始化&#xff0c;叫常…
阅读更多...
机器学习-线性回归（参数估计之经验风险最小化）

机器学习-线性回归（参数估计之经验风险最小化）

给定一组包含 &#x1d441; 个训练样本的训练集 我们希望能够 学习一个最优的线性回归的模型参数 &#x1d498; 现在我们来介绍线性回归的一种模型参数估计方法&#xff1a;经验风险最小化。 我们前面说过&#xff0c;对于标签 &#x1d466; 和模型输出都为连续的实数值&…
阅读更多...
appium自动化环境搭建

appium自动化环境搭建

一、appium介绍 appium介绍 appium是一个开源工具、支持跨平台、用于自动化ios、安卓手机和windows桌面平台上面的原生、移动web和混合应用&#xff0c;支持多种编程语言(python&#xff0c;java&#xff0c;Ruby&#xff0c;Javascript、PHP等) 原生应用和混合应用&#xf…
阅读更多...
视频多模态模型——视频版ViT

视频多模态模型——视频版ViT

大家好&#xff0c;这里是好评笔记&#xff0c;公主号&#xff1a;Goodnote&#xff0c;专栏文章私信限时Free。本文详细解读多模态论文《ViViT: A Video Vision Transformer》&#xff0c;2021由google 提出用于视频处理的视觉 Transformer 模型&#xff0c;在视频多模态领域有…
阅读更多...
使用Cline+deepseek实现VsCode自动化编程

使用Cline+deepseek实现VsCode自动化编程

不知道大家有没有听说过cursor这个工具&#xff0c;类似于AIVsCode的结合体&#xff0c;只要绑定chatgpt、claude等大模型API&#xff0c;就可以实现对话式自助编程&#xff0c;简单闲聊几句便可开发一个软件应用。 但cursor受限于外网&#xff0c;国内用户玩不了&#xff0c;…
阅读更多...
【Linux】Linux编译器-g++、gcc、动静态库

【Linux】Linux编译器-g++、gcc、动静态库

只要积极创造&#xff0c;机遇无时不有&#xff1b;只要善于探索&#xff0c;真理无处不在。&#x1f493;&#x1f493;&#x1f493; 目录 ✨说在前面 &#x1f34b;知识点一&#xff1a;Linux编译器-g、gcc •&#x1f330;1. 背景知识 •&#x1f330;2. gcc如何完成 •…
阅读更多...
Spring整合Mybatis、junit纯注解

Spring整合Mybatis、junit纯注解

如何创建一个Spring项目 错误问题 不知道什么原因&#xff0c;大概是依赖版本不兼容、java版本不对的问题&#xff0c;折磨了好久就是搞不成。 主要原因看pom.xml配置 pom.xml配置 java版本 由于是跟着22年黑马视频做的&#xff0c;java版本换成了jdk-11&#xff0c;用21以…
阅读更多...
【架构面试】二、消息队列和MySQL和Redis

【架构面试】二、消息队列和MySQL和Redis

MQ MQ消息中间件 问题引出与MQ作用 常见面试问题&#xff1a;面试官常针对项目中使用MQ技术的候选人提问&#xff0c;如如何确保消息不丢失&#xff0c;该问题可考察候选人技术能力。MQ应用场景及作用&#xff1a;以京东系统下单扣减京豆为例&#xff0c;MQ用于交易服和京豆服…
阅读更多...
MATLAB提供的颜色映射表colormap——伪彩色

MATLAB提供的颜色映射表colormap——伪彩色

图像处理领域的一个习惯&#xff1a;不是真实的颜色&#xff0c;一般用伪彩色。一是说明不是物体本身的颜色&#xff0c;二是彩色更容易分辨。 MATLAB陆续提供了16种颜色映射表colormap。 之前的都很丑&#xff0c;近5年新增的4种还可以。总的说来还是丑。 这是一种鸟的名字。…
阅读更多...
案例研究丨浪潮云洲通过DataEase推进多维度数据可视化建设

案例研究丨浪潮云洲通过DataEase推进多维度数据可视化建设

浪潮云洲工业互联网有限公司&#xff08;以下简称为“浪潮云洲”&#xff09;成立于2018年&#xff0c;定位于工业数字基础设施建设商、具有国际影响力的工业互联网平台运营商、生产性互联网头部服务商。截至目前&#xff0c;浪潮云洲工业互联网平台连续五年入选跨行业跨领域工…
阅读更多...
电脑无法开机，重装系统后没有驱动且驱动安装失败

电脑无法开机，重装系统后没有驱动且驱动安装失败

电脑无法开机&#xff0c;重装系统后没有驱动且驱动安装失败 前几天电脑突然坏了&#xff0c;电脑卡住后&#xff0c;强制关机&#xff0c;再开机后开机马上就关机。尝试无数次开机后失败&#xff0c;进入BIOS界面&#xff0c;发现已经没有Windows系统了。重新安装系统后&…
阅读更多...
C++异步future

C++异步future

&#x1f30e; C11异步futrue 文章目录&#xff1a; C11异步futrue future介绍     应用场景     future操作       std::async函数模版       std::packaged_task类模版       std::promise类模版 &#x1f680;future介绍 std::future是C11标准库…
阅读更多...
【C++探索之路】STL---string

【C++探索之路】STL---string

走进C的世界&#xff0c;也意味着我们对编程世界的认知达到另一个维度&#xff0c;如果你学习过C语言&#xff0c;那你绝对会有不一般的收获&#xff0c;感受到C所带来的码云风暴~ ---------------------------------------begin--------------------------------------- 什么是…
阅读更多...
CF 339A.Helpful Maths(Java实现)

CF 339A.Helpful Maths(Java实现)

题目分析 输入一串式子&#xff0c;输出从小到大排列的式子 思路分析 如上所说核心思路&#xff0c;但是我要使用笨方法&#xff0c;输入一串式子用split分割开&#xff0c;但是此时需要用到转义字符&#xff0c;即函数内参数不能直接使用“”&#xff0c;而是“\\”。分割开后…
阅读更多...
C#，入门教程(07)——软件项目的源文件与目录结构

C#，入门教程(07)——软件项目的源文件与目录结构

上一篇&#xff1a; C#&#xff0c;入门教程(06)——解决方案资源管理器&#xff0c;代码文件与文件夹的管理工具https://blog.csdn.net/beijinghorn/article/details/124895033 创建新的 C# 项目后&#xff0c; Visual Studio 会自动创建一系列的目录与文件。 程序员后面的工…
阅读更多...
Cpp::静态 动态的类型转换全解析(36)

Cpp::静态 动态的类型转换全解析(36)

文章目录 前言一、C语言中的类型转换二、为什么C会有四种类型转换&#xff1f;内置类型 -> 自定义类型自定义类型 -> 内置类型自定义类型 -> 自定义类型隐式类型转换的坑 三、C强制类型转换static_castreinterpret_castconst_castdynamic_cast 四、RTTI总结 前言 Hell…
阅读更多...
Android中Service在新进程中的启动流程

Android中Service在新进程中的启动流程

目录 1、Service与AMS交互框架介绍 1.1、认识AMS代表IActivityManager 1.2、认识客户端代表IApplicationThread 2、Service启动流程概览 我们知道Android有四大组件&#xff0c;Activity、Service、ContentProvider、Broadcast&#xff0c;每个组件在系统运行中或者我们编写…
阅读更多...
docker 简要笔记

docker 简要笔记

文章目录 一、前提内容1、docker 环境准备2、docker-compose 环境准备3、流程说明 二、打包 docker 镜像1、基础镜像2、国内镜像源3、基础的dockerfile4、打包镜像 四、构建运行1、docker 部分2、docker-compose 部分2.1、构建docker-compose.yml2.1.1、同目录构建2.1.2、利用镜…
阅读更多...
利用Redis实现数据缓存

利用Redis实现数据缓存

目录 1 为啥要缓存捏&#xff1f; 2 基本流程&#xff08;以查询商铺信息为例&#xff09; 3 实现数据库与缓存双写一致 3.1 内存淘汰 3.2 超时剔除&#xff08;半自动&#xff09; 3.3 主动更新&#xff08;手动&#xff09; 3.3.1 双写方案 3.3.2 读写穿透方案 3.3.…
阅读更多...
最新文章
推荐文章

Copyright @ 2022~2023