文章目录
- 残差结构的一般表达形式
- 残差结构中的信息传播
- clean path propagation
- 前向传播
- 反向传播
- h(x)为恒等映射的重要性
- h(x)的实验证明
- 激活层的位置
- 和其他网络的对比
上一篇讲了 ResNet 论文中的第一篇:Deep Residual Learning for Image Recognition,主要是介绍了残差网络解决了网络随着深度的增加而带来的退化问题;介绍了残差的概念及两种残差结构;最后通过丰富的实验来证明残差结构对增加网络深度,增强表达能力的准确率有足够的优化作用,而且不会带来网络退化的问题。
这一篇来说说 ResNet 论文的第二篇:Identity Mappings in Deep Residual Networks。这一篇主要描述了在标准的残差公式中,为什么能解决退化问题,其背后的逻辑是什么,而且还说明了为什么要使用恒等映射;最后讨论了一下残差结构中激活层的一些问题。
原文的描述是:In this paper, we analyze the propagation formu- lations behind the residual building blocks, which suggest that the for- ward and backward signals can be directly propagated from one block to any other block。
残差结构的一般表达形式
在上一篇中,提到了残差结构:
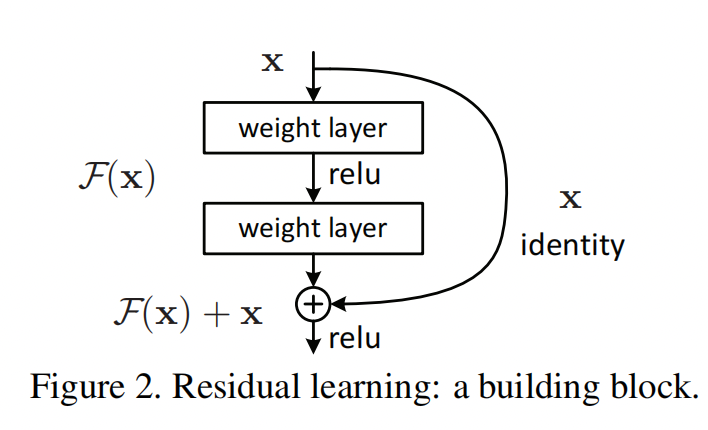
在这篇论文中提供了一个更加细化一点的形式:
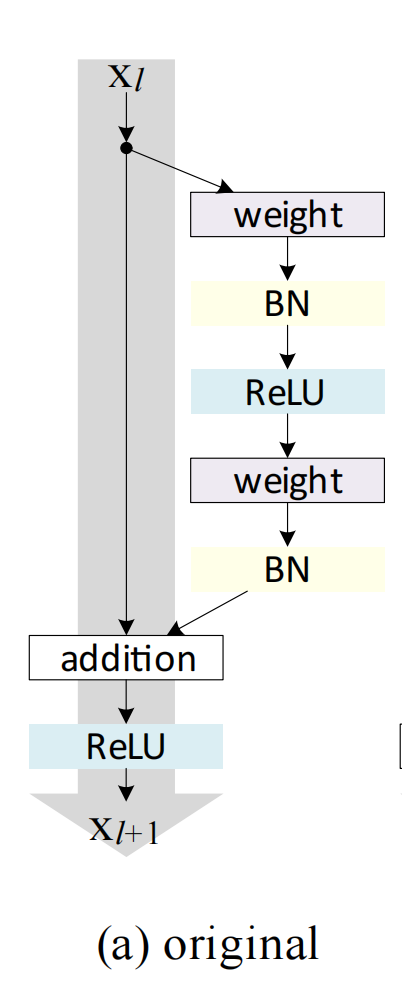
对这个结构抽象出来一个一般化的描述公式:
y l = h ( x l ) + F ( x l , W l ) y_l=h(x_l) + F(x_l, W_l) yl=h(xl)+F(xl,Wl)
x x + 1 = f ( y l ) x_{x+1}=f(y_l) xx+1=f(yl)
其中:
- x l x_l xl 为残差结构的输入, x l + 1 x_{l+1} xl+1 为残差结构的输出。
- F ( x l , W l ) F(x_l, W_l) F(xl,Wl) 为残差部分,根据上一篇文章的分析,也就是卷积层部分。
- h ( x l ) h(x_l) h(xl) 是 shortcut connection(或者是叫做 direct path,还有就是称作 skip connections,都是一个意思)对输入 x l x_l xl 的映射函数。上一篇的结构中,这个函数就被定义为 identity mapping,也被称为恒等映射。这一篇还会证明说这个是最好的选择。
- y l y_l yl 就是残差与 shortcut connection mapping 相加。然后映射 f f f 就是对这个输出 y l y_l yl 的激活层处理,在上一篇中使用的函数定义是 ReLU 激活层。当然也可以是其他处理方式,具体使用那种处理方式也是这一篇要讨论的重点,这个建议也是使用恒等映射,后面章节会进行说明。
通过上面的公式和简单的说明,可以了解到这篇文章的主要内容就是解释和说明三个问题:
- 为什么残差结构可以保证信息在正向和反向传播中保证信息(梯度)的传递,而且要尽量保持这条 skip connection 通路的畅通,文中叫做 clean information path。
- 为了保证获得 clean information path,论文提出了两个条件,或者说两个建议。第一个就是上面公式中的 h h h 映射要使用恒等映射。
- 第二个就是上面公式中的 f f f 也要采用恒等映射。通过这样两个手段来保证信息可以自由的传播。
- F F F 作为残差结构,就是卷积层的设计了。一般来说就是前一篇中提到的两种残差结构之一了。
残差结构中的信息传播
clean path propagation
为了证明函数映射 h h h和 f f f都是使用恒等映射最好,论文中是采用了反证法。
论文中假设这两个函数都是使用的恒等映射,再证明如果不是恒等映射的话,性能肯定比恒等映射差。
如果两个函数是恒等映射的话,上面的公式就可以简化为:
y l = x l + F ( x l , W l ) y_l=x_l + F(x_l, W_l) yl=xl+F(xl,Wl)
x x + 1 = y l x_{x+1}=y_l xx+1=yl
也就是可以合并为:
x x + 1 = x l + F ( x l , W l ) x_{x+1}=x_l + F(x_l, W_l) xx+1=xl+F(xl,Wl)
前向传播
因为这个残差结构是一个可重叠的模块,那么假设从输入到输出之间总共有 L L L个residual block。那么最后的输出就可以由公式:
x L = x l + ∑ i = l L F ( x i , W i ) x_L=x_l+\sum_{i=l}^LF(x_i,W_i) xL=xl+i=l∑LF(xi,Wi)
简单的来说,深处网络的输出就是最初的输入加上各个卷积层构造的残差之和。
而如果是plain network的话,如果忽略掉激活层,输出应该是各个卷积层的矩阵的乘积:
x L = ∏ i = l L W i x l x_L=\prod_{i=l}^LW_ix_l xL=i=l∏LWixl
我的理解,这里的优势在于连乘会导致一些信息丢失,会变得很大或者很小。而连加的连续性和趋势就会好很多。
这样就可以比较方便的进行优化,去掉一些残差结构,增加一些残差结构,只是在残差值上有一些比较缓和的变化。
反向传播
在讨论反向传播时,假设输出层的损失值为 ϵ \epsilon ϵ。
那么在梯度反向传播时,通过求导的链式法则:
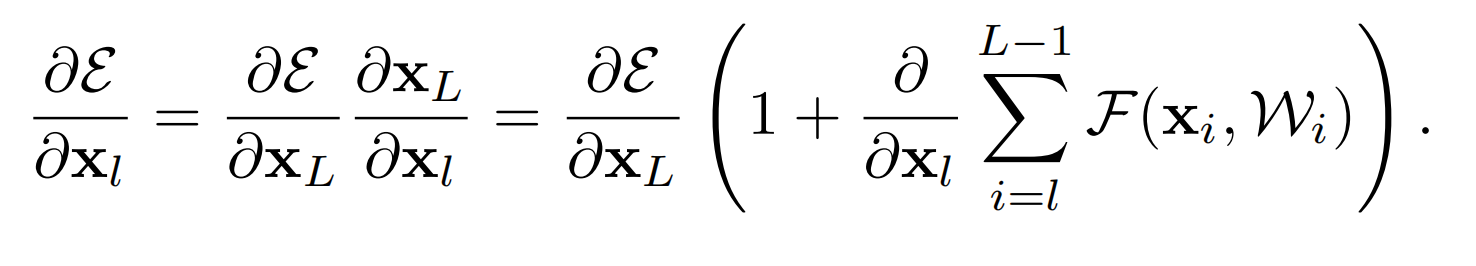
这个公式可以看成两个部分:
- 第一部分是 ∂ ϵ ∂ L \frac{\partial{\epsilon}}{\partial L} ∂L∂ϵ,这部分梯度的传播之和层数L有关,和卷积层没有关系,所以和正向传播类似,这部分梯度信息可以在层与层之间顺利的传播。
- 更重要的,第二部分 ∂ ∂ l ∑ i = l L − 1 F ( x i , W i ) \frac{\partial}{\partial l}\sum_{i=l}^{L-1} F(x_i, W_i) ∂l∂∑i=lL−1F(xi,Wi),这部分不可能对于每个样本都会计算得到-1(如果是-1的话,梯度就等于0了,相当于就是梯度消失的情况),所以再加上前面的 ∂ ϵ ∂ L \frac{\partial{\epsilon}}{\partial L} ∂L∂ϵ这一部分,就能保证梯度在反向传播的时候顺利的在层与层之间进行传播。
h(x)为恒等映射的重要性
论文接下来的部分就是通过反证法来证明使用恒等映射的必要性。
首先是 h ( x ) h(x) h(x),如果 h ( x ) h(x) h(x)不是恒等映射,而是扩展为一种稍微复杂一点的形式:
h ( x ) = λ x l h(x) = \lambda x_l h(x)=λxl
同时, f ( x ) f(x) f(x)还保持恒等映射。
那么,每个残差结构的映射关系就变成:
x l + 1 = λ x l + F ( x l , W l ) x_{l+1}=\lambda x_l + F(x_l, W_l) xl+1=λxl+F(xl,Wl)
正向传播的公式就会为:
x L = ( ∏ i = l L − 1 λ ) x l + ∑ i = l L F ^ ( x i , W i ) x_L=(\prod_{i=l}^{L-1} \lambda) x_l + \sum_{i=l}^L \hat{F}(x_i,W_i) xL=(i=l∏L−1λ)xl+i=l∑LF^(xi,Wi)
反向传播的公式就是:
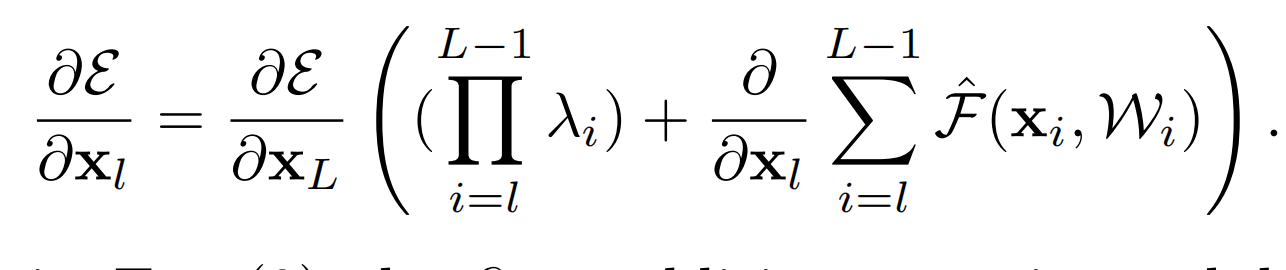
这里出现了一个梯度连乘的部分。这部分影响非常大:
- 如果 λ > 1 \lambda > 1 λ>1,那么经过多层之后,连乘的效应会将梯度变得很大,这就是梯度爆炸。
- 如果 λ < 1 \lambda < 1 λ<1,那么经过多层之后,连乘的效应会将梯度变得很小,这就是梯度消失。
- 论文中还提到,如果 h ( x ) h(x) h(x)是更复杂的函数,那么同样会导致梯度在层与层之间的传播。我的理解就是越复杂,越不可控,越容易出问题,也越难优化。文中是通过实验比对来证明这个结果的,原文为:In the above analysis, the original identity skip connection in Eqn.(3) is replaced with a simple scaling h(xl) = λlxl If the skip connection h(xl) represents more complicated transforms (such as gating and 1×1 convolutions), in Eqn.(8)the first term becomes Q L−1 i=l h0i where h0 is the derivative of h. This product may also impede information propagation and hamper the training procedure as witnessed in the following experiments
- 所以,恒等映射是最好的选择。
h(x)的实验证明
论文中做了下面几种实验:
- 使用普通的 λ \lambda λ,也就是Constant scaling,而且这个还做了一下细分
- 令 λ = 0.5 \lambda = 0.5 λ=0.5,而且在残差部分也乘上了 1 − λ = 0.5 1-\lambda = 0.5 1−λ=0.5。
- 令 λ = 0 \lambda = 0 λ=0,而且在残差部分也乘上了 1 − λ = 1 1-\lambda = 1 1−λ=1。
- 令 λ = 1 \lambda = 1 λ=1,而且在残差部分也乘上了 1 − λ = 0 1-\lambda = 0 1−λ=0。
结果如下:

- 令 h ( x ) h(x) h(x)为一个门网络(另外一片论文中提出的),也就是 h ( x ) = g ( x ) x l h(x)=g(x) x_l h(x)=g(x)xl, g ( x ) g(x) g(x)是一个1 * 1的卷积层。所以文中提到的公式是: 1 1 + e − x ( W g x + b g ) \frac{1}{1+e^{-x}(W_gx+b_g)} 1+e−x(Wgx+bg)1这个公式一看就是卷积层加softmax激活层。然后是残差结构这边乘以g(x),skip connection那边是乘以 1 − g ( x ) 1-g(x) 1−g(x)。
实验结果如下:

图中的 b ( g ) b(g) b(g)是门网络中需要优化的一种初始化方法,不重要。
- 还有就是只把这个 g ( x ) g(x) g(x)应用到 h ( x ) h(x) h(x)上,残差结构不动,结果如下:

- 最后是使用1 * 1的卷积层和dropout方法。全部的结果如下:

最后关于1 * 1卷积层的一点是,使用卷积层应该是可以提升网络的表达能力的,但是因为引入卷积层的原因导致了退化问题,这部分退化问题导致的效果把表达能力这部分带来的效果给覆盖掉了。我觉得潜台词就是如果网络比较浅的话,这里可以使用1 * 1的卷积层。
激活层的位置
接下来就就是分析 f ( x ) f(x) f(x),通过这篇论文的分析, f ( x ) f(x) f(x)使用恒等映射更好,而在前一篇里实际上是 f ( x ) = R e L U f(x) = ReLU f(x)=ReLU的。所以作者就琢磨是通过把这个ReLU层给挪个位置来实现这个恒等映射。
总共考虑了5种方式,这5种方式的验证实验室在101(2个3 * 3的那种残差结构)和164(1 * 1 + 3 * 3 + 1 * 1的这种叫做bottlenect的残差结构):

- BN after addition,把BN层也从残差结构中挪到 f ( x ) f(x) f(x)中来。起到的是反作用。
- ReLU before addition,把origin中的ReLU挪到了残差结构中,实现了 f ( x ) f(x) f(x)的恒等映射。但是效果也不好。看文中的意思是因为BN层改变了卷积后的分布,导致性能下降。
- 我理解d和e的区别就是上一层的残差结构的输出是否需要先做BN,或者说先BN再加还是先加再BN。从实验结果来看,还是最后一种的效果要好一些。
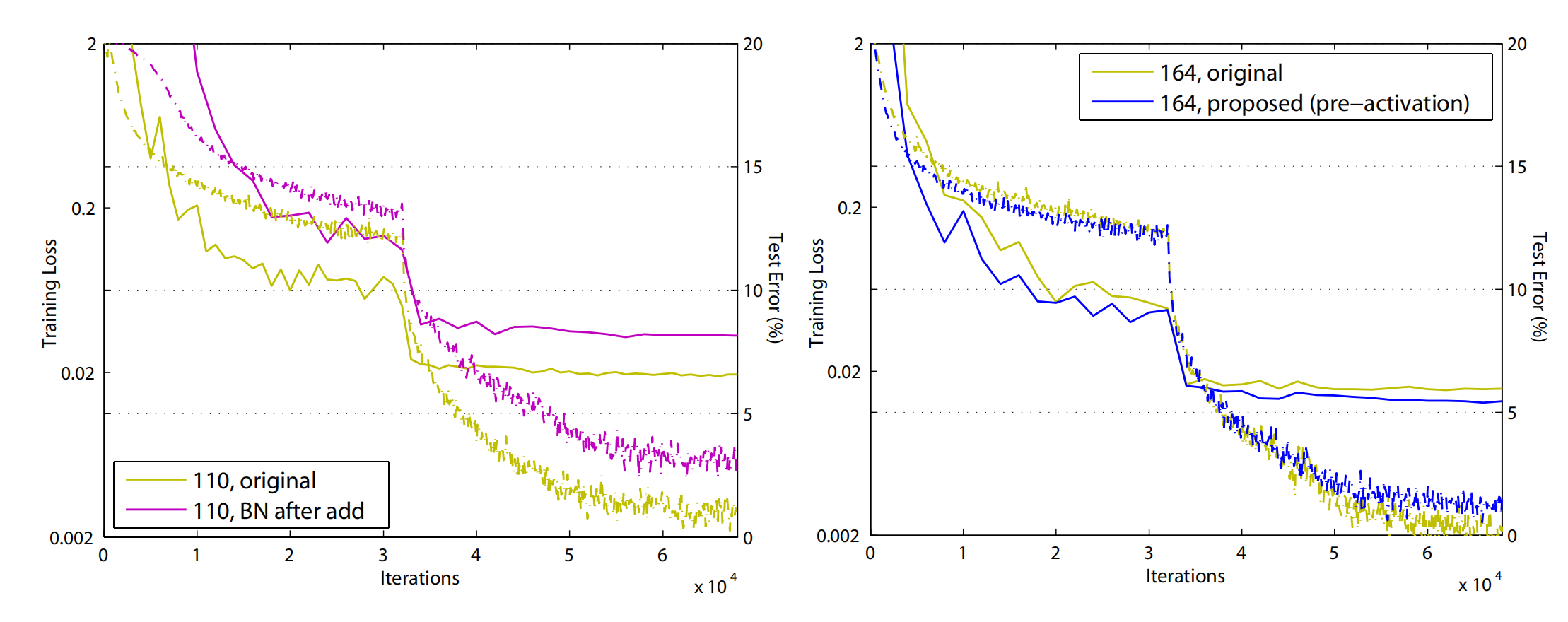
然后还测试了一下最后一种效果在各个深度的网络上的结果,效果很好,而且还得到了解决过拟合问题的效果。
从图上看,相对于origin的版本,训练精度稍低,但是测试精度要高一些。
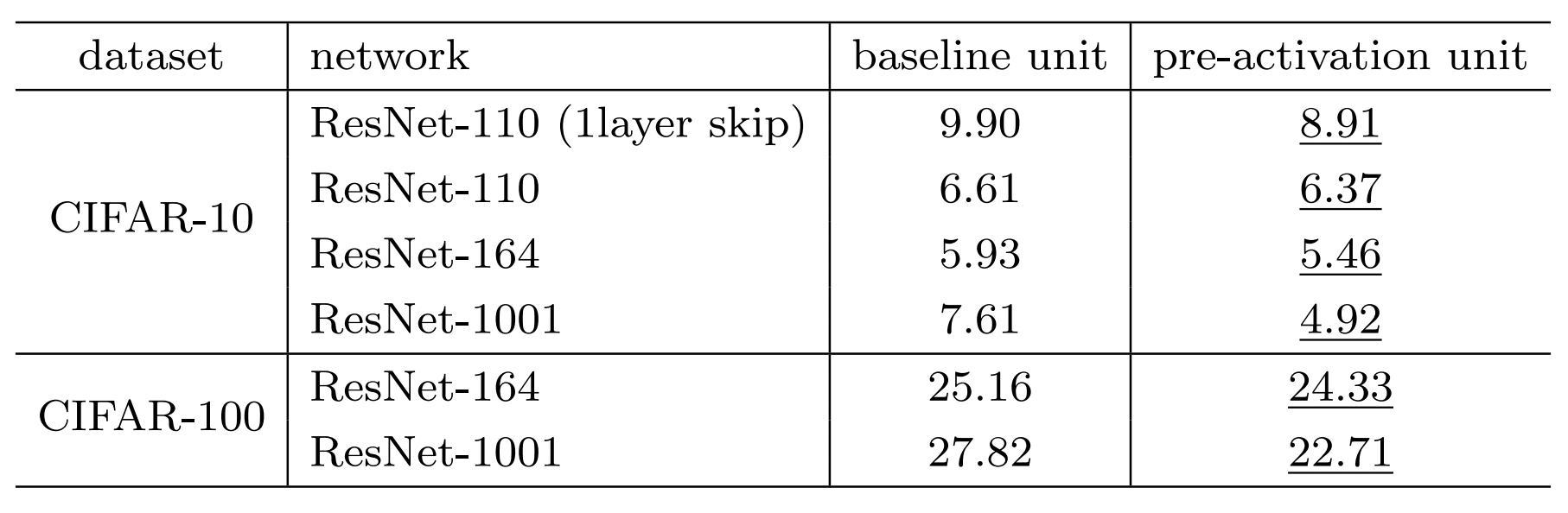
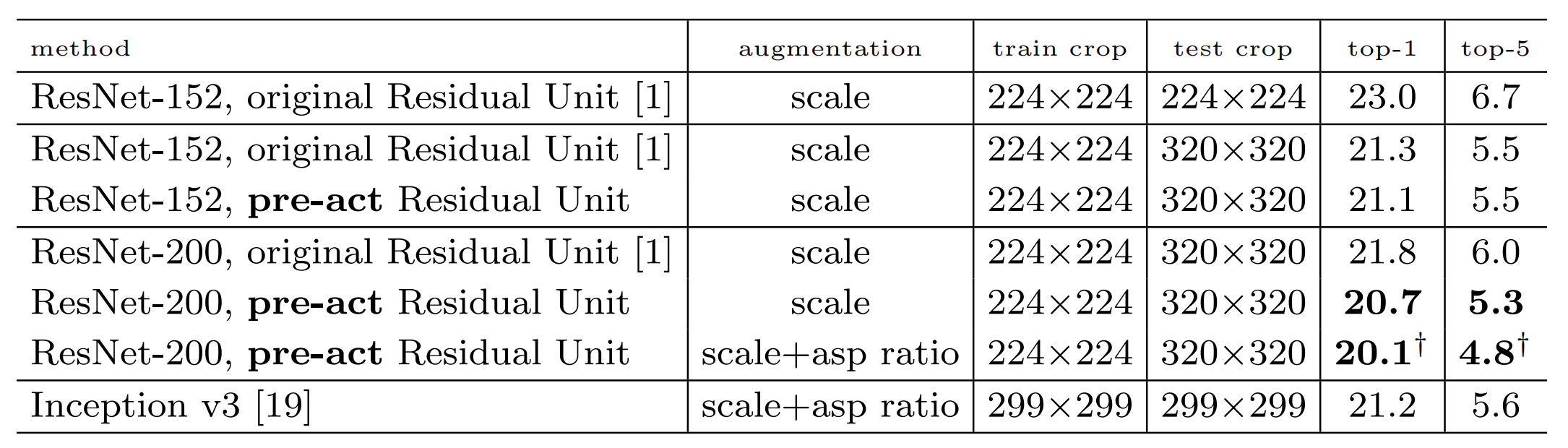
和其他网络的对比
最后,提供了一份综合的对比结果,在ILSVRC 2012验证集上的结果。