










clc
clear
n = 300; % 定义表示森林的矩阵大小
Plight = 5e-6; Pgrowth = 1e-2; % 定义闪电和生长的概率
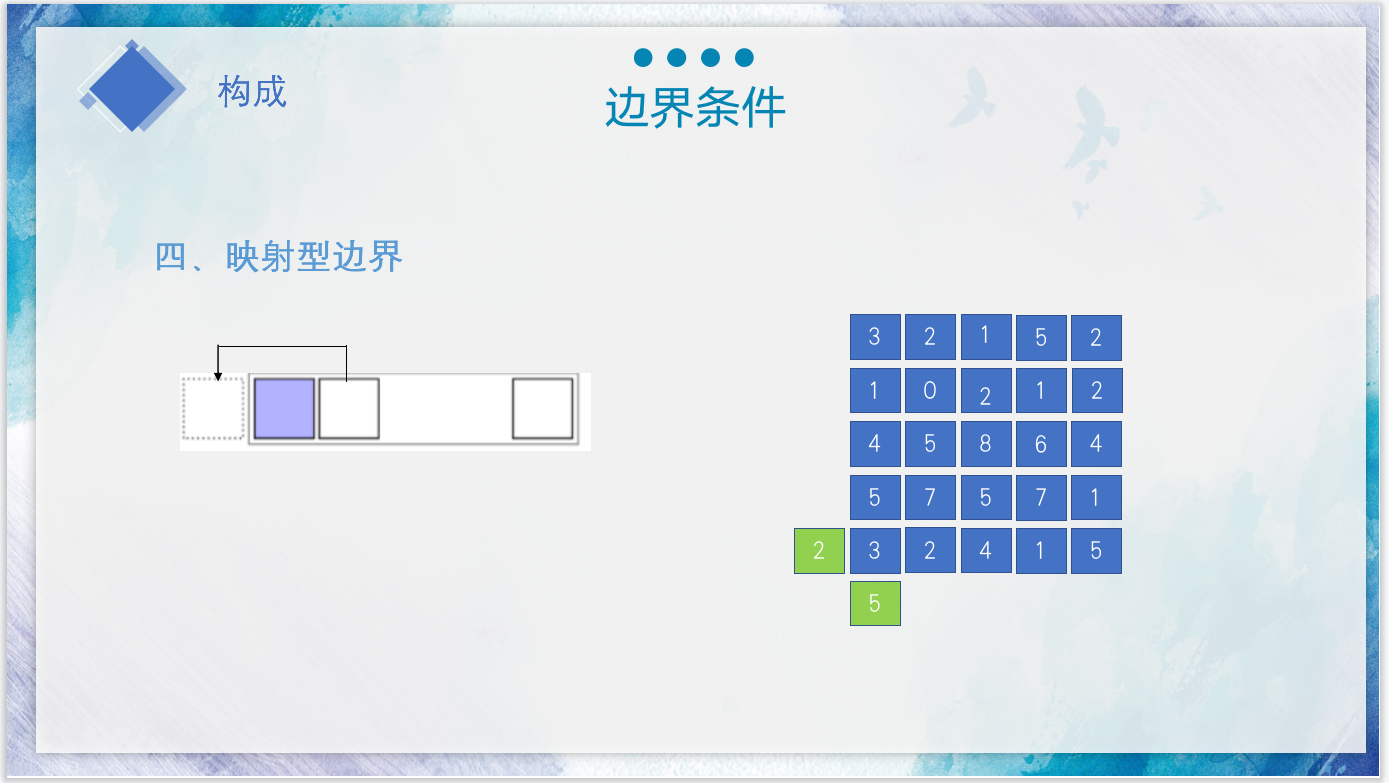
UL = [n,1:n-1]; DR = [2:n,1]; % 定义上左,下右邻居
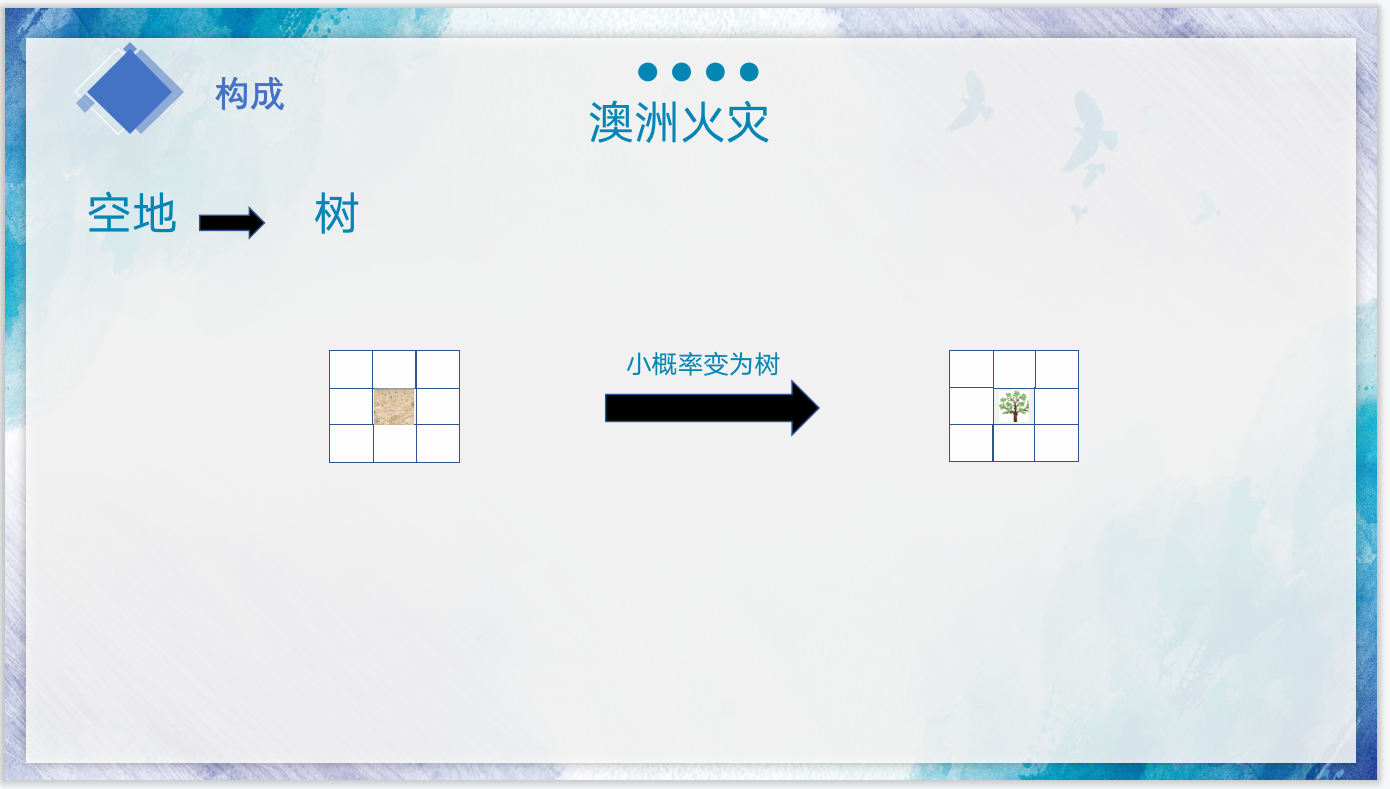
veg=zeros(n,n); % 初始化表示森林的矩阵
imh = image(cat(3,veg,veg,veg)); % 可视化表示森林的矩阵
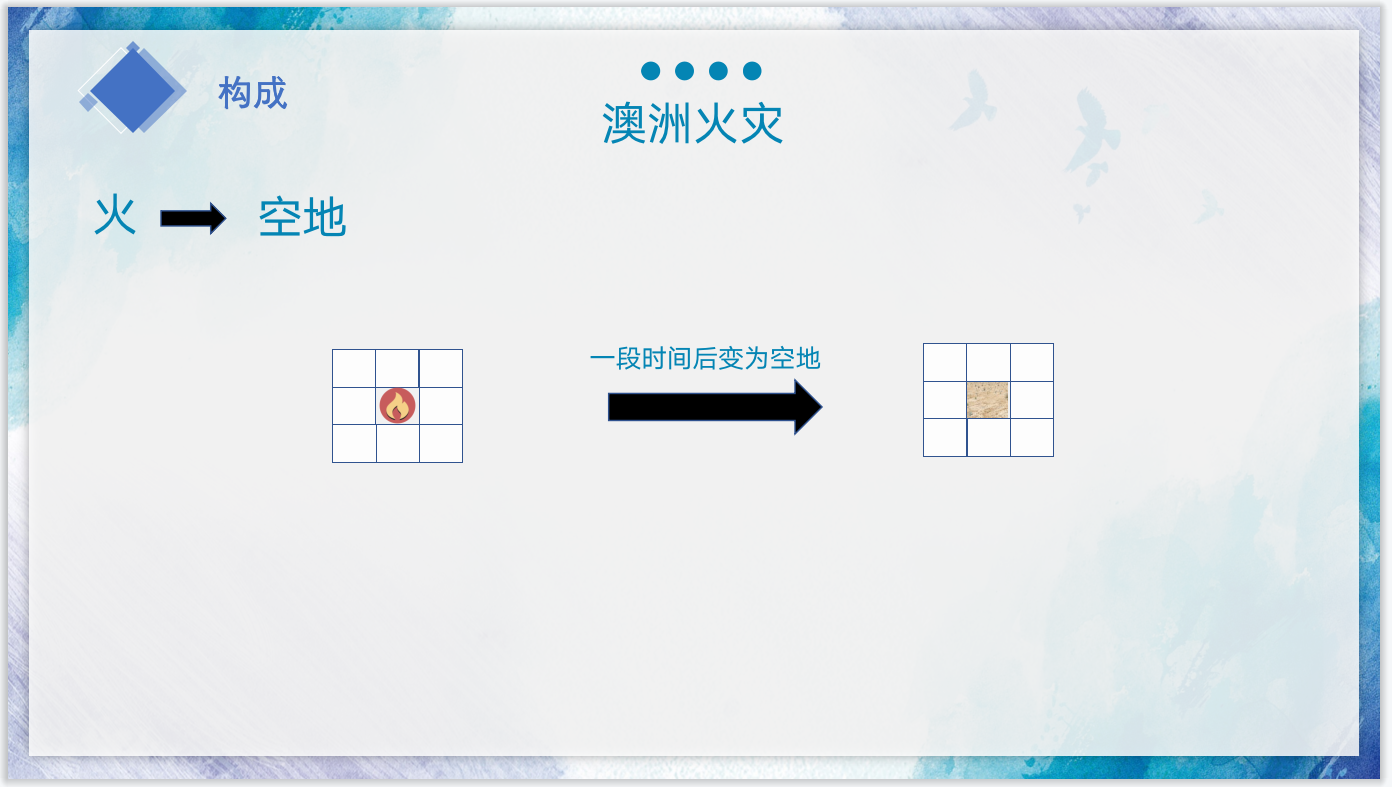
% veg = 空地为0 着火为1 树木为2
for i=1:3000 sum =(veg(UL,:)==1) + (veg(:,UL)==1)+(veg(:,DR)==1) + (veg(DR,:)==1); % 计算出所有格子有几个邻居是着火的
% 根据规则更新森林矩阵:是否树=是否树-是否着火的树+是否新生的树(0-1运算)veg = 2*(veg==2) - ( (veg==2) & (sum>0 |(rand(n,n)<Plight)) ) +2*((veg==0) & rand(n,n)<Pgrowth) ; set(imh, 'cdata', cat(3,(veg==1),(veg==2),zeros(n)) )drawnow % 可视化表示森林的矩阵
end
clc
clear all;
n=200;
Se=zeros(n);
Z=zeros(n)
Se(n/2-2:n/2+2,n/2-2:n/2+2)=1;
Ch=imagesc(cat(3,Se,Z,Z));
axis square
Sd=zeros(n+2);
while(1)Sd(2:n+1,2:n+1)=Se;sum=Sd(1:n,2:n+1)+Sd(3:n+2,2:n+1)+Sd(2:n+1,1:n)+Sd(2:n+1,3:n+2);Se=mod(sum,2);set(Ch,'cdata',cat(3,Se,Z,Z))pause(0.05)
endfigure
clc
clear;
n=200;
p=0.4;
z=zeros(n)
Se=rand(n)<p;
Sd=zeros(n+2);%矩阵初始化
Ph=image(cat(3,Se,z,z));%初始可视化
while(1)Sd(2:n+1,2:n+1)=Se;%Sum=Sd(1:n,2:n+1)+Sd(3:n+2,2:n+1)+Sd(2:n+1,1:n)+Sd(2:n+1,3:n+2)+Sd(1:n,1:n)+Sd(3:n+2,1:n)+Sd(1:n,3:n+2)+Sd(3:n+2,3:n+2);
%邻居之和(邻居中生的元胞的数目)for i=1:nfor j=1:nif Sum(i,j)==3||(Sum(i,j)==2&&Se(i,j)==1)%生的条件Se(i,j)=1;else Se(i,j)=0;endend
end
set(Ph,'cdata',cat(3,Se,z,z))%更新可视化drawnow
end