【使用 DSP 滤波器加速速度和位移】使用信号处理算法过滤加速度数据并将其转换为速度和位移研究（Matlab代码实现）

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

💥1 概述

📚2 运行结果

🎉3 参考文献

🌈4 Matlab代码实现

💥1 概述

对于实时采集的加速度数据，可以应用信号处理算法，如数字滤波和积分运算，将其转换为速度和位移数据。下面是一个简要的概述：

1. 数据采集：首先需要进行数据采集，通过传感器获取物体的加速度数据。这可以通过加速度计等传感器来实现，例如使用微电机惯性测量单元（IMU）或加速度传感器。

2. 数字滤波：为了去除噪声和不必要的高频分量，可以应用数字滤波技术，如低通滤波器。常见的滤波器类型包括巴特沃斯滤波器、无限脉冲响应（IIR）滤波器和有限脉冲响应（FIR）滤波器。滤波后的信号将更加平滑和稳定。

3. 数值积分：将经过滤波的加速度信号积分一次，可以得到速度信号。数值积分是通过近似求解离散点间的微分来实现的。积分操作会导致积分误差的累积，因此需要考虑误差修正和积分漂移校准的方法。

4. 二次积分：将经过滤波和积分的速度信号再次积分，可以得到位移信号。同样，二次积分也会引入积分误差的累积，因此需要对误差进行校正和修正。

5. 校准和校正：为了获得准确的结果，可能需要进行传感器的校准和校正。这包括零偏校准、灵敏度校准和加速度计的温度效应校正等。

需要注意的是，将加速度数据转换为速度和位移的过程是一个近似计算，其中存在积分误差的累积，尤其是在长时间的测量中。因此，在进行精确位移测量时，需要考虑积分误差的校准和修正。

总结来说，将加速度数据转换为速度和位移的过程包括数据采集、数字滤波、数值积分和二次积分。每个步骤都需要选择合适的算法和参数，并进行校准和修正，以获得准确可靠的速度和位移结果。

📚2 运行结果

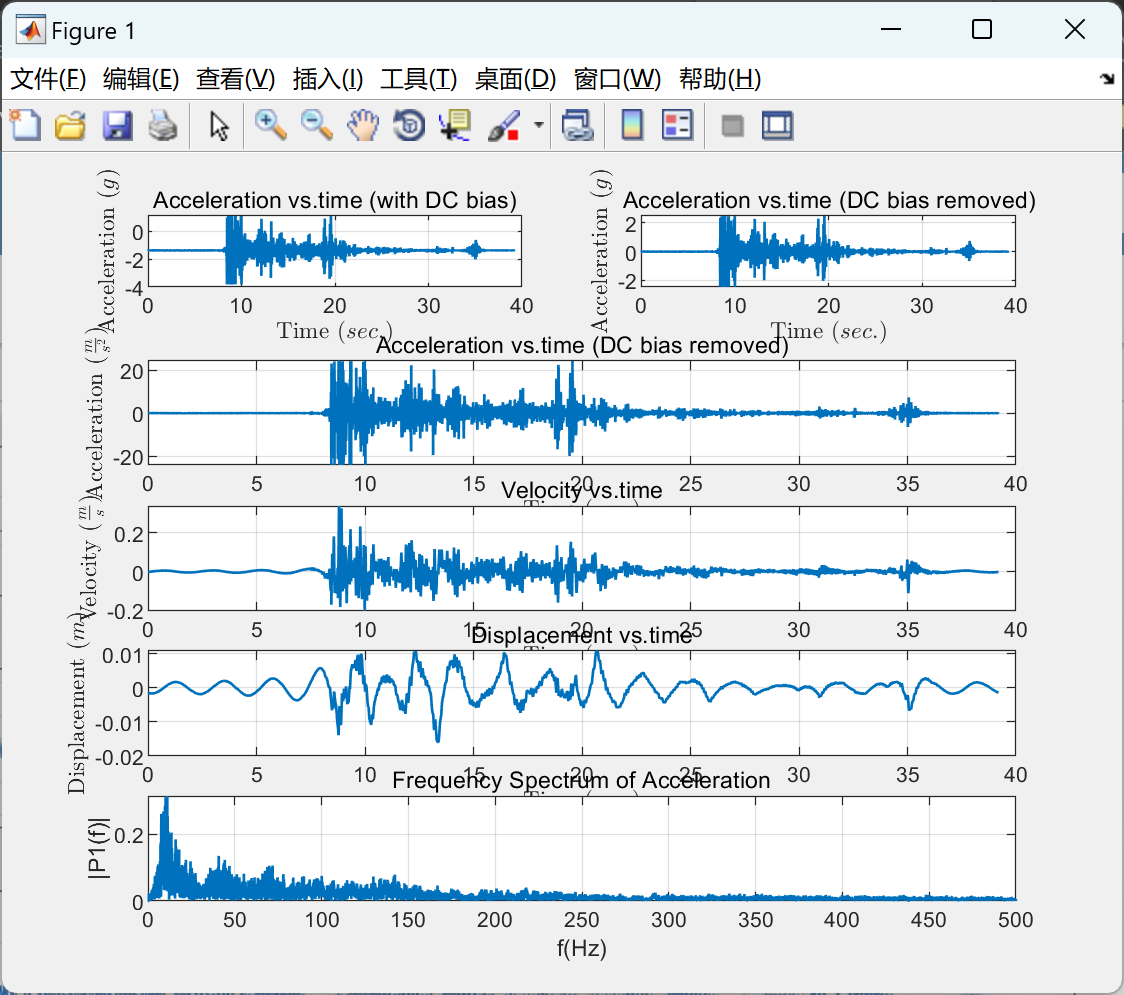
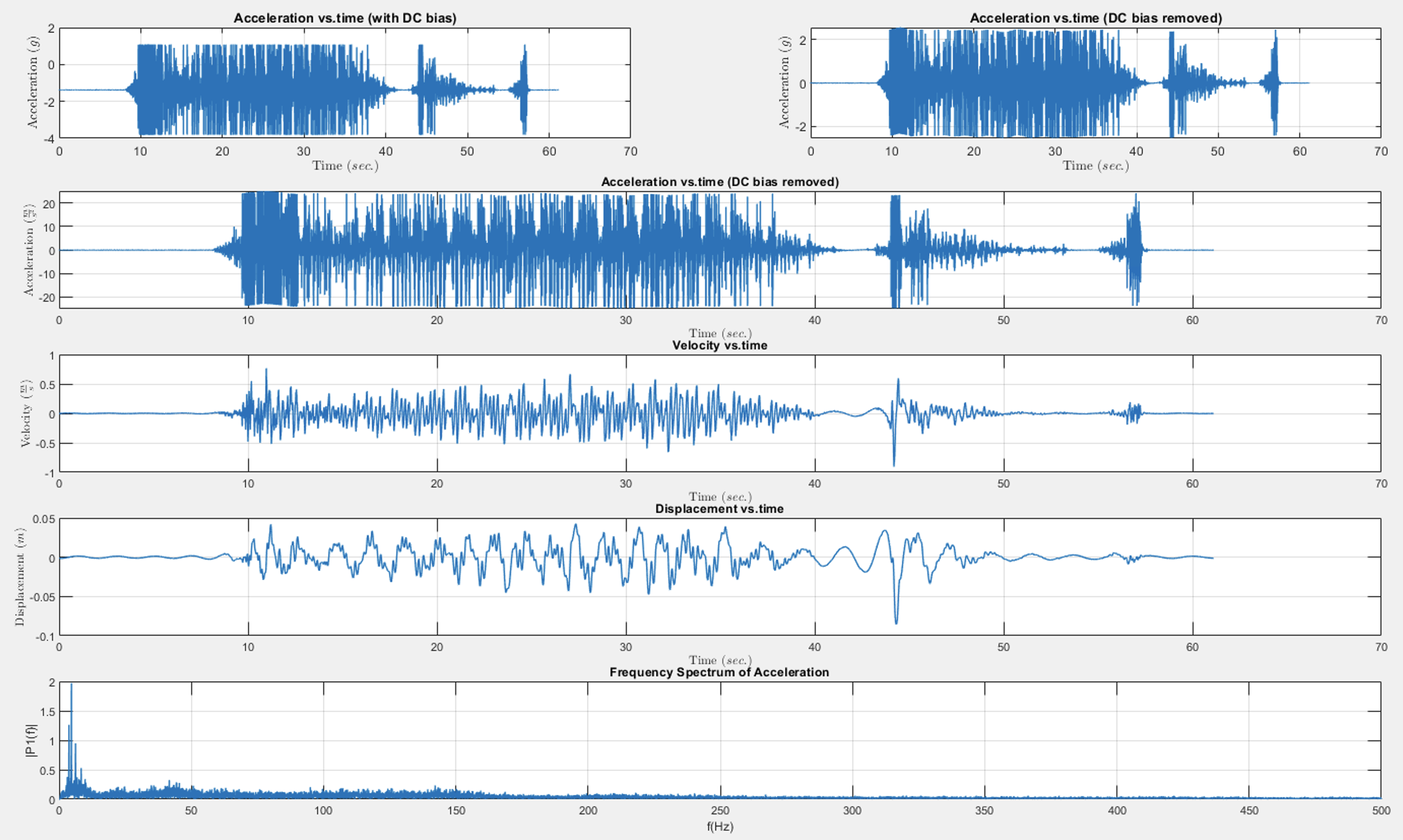
部分代码：

%% Processed inputs
%--------------------------------------------------------------------------
time = data(:,1); % Time vector
accval_g = data(:,2); % Acceleration in g
accval = data(:,2)*9.81; % Acceleration in m/s^2
L = size(data,1); % Length of signal
Fs = 1/(time(2)-time(1)); % Sampling frequency
Ts = 1/Fs; % Sampling period

%% Displacement, Velocity and Acceleration
%--------------------------------------------------------------------------
[~, ~, ~, filtered_acc_g] ...
= accelo2disp(time,Ts, Fs, Fcut,alpha, accval_g, Lvdtmat,...
lvdtcons, accbiasV, accsensi, filtertype...
,filtermethod,firorder);

[LVDTfilt, filtered_disp, filtered_vel, filtered_acc] ...
= accelo2disp(time,Ts, Fs, Fcut,alpha, accval, Lvdtmat,...
lvdtcons, accbiasV, accsensi, filtertype...
,filtermethod,firorder);

%% Compute the frequency
%--------------------------------------------------------------------------
% Compute the Fourier transform of the signal.
Y = fft(filtered_acc);

% Compute the two-sided spectrum P2. Then compute the single-sided spectrum P1
% based on P2 and the even-valued signal length L.
P2 = abs(Y/L);
P1 = P2(1:L/2+1);
P1(2:end-1) = 2*P1(2:end-1);

% Define the frequency domain f and plot the single-sided amplitude spectrum P1.
% On average, longer signals produce better frequency approximations.
f = Fs*(0:(L/2))/L;

%% Plot Acceleration vs.time
%--------------------------------------------------------------------------
figure;
subplot(5,2,1)
ax1 = plot(time, accval_g, 'LineWidth', 1);
grid on
xlabel('Time ($sec.$)','Interpreter', 'latex');
ylabel('Acceleration ($g$)','Interpreter', 'latex');
title('Acceleration vs.time (with DC bias)')

ax2 = subplot(5,2,2);
plot(time, filtered_acc_g, 'LineWidth', 1)
grid on
xlabel('Time ($sec.$)','Interpreter', 'latex');
ylabel('Acceleration ($g$)','Interpreter', 'latex');
title('Acceleration vs.time (DC bias removed)')

ax3 = subplot(5,2,3:4);
plot(time,filtered_acc, 'LineWidth', 1)
grid on
xlabel('Time ($sec.$)','Interpreter', 'latex');
ylabel('Acceleration ($\frac{m}{s^2}$)','Interpreter', 'latex');
title('Acceleration vs.time (DC bias removed)')

ax4 = subplot(5,2,5:6);
plot(time,filtered_vel, 'LineWidth', 1)
grid on
xlabel('Time ($sec.$)','Interpreter', 'latex');
ylabel('Velocity ($\frac{m}{s}$)','Interpreter', 'latex');
title('Velocity vs.time')

ax5 = subplot(5,2,7:8);
plot(time,filtered_disp, 'LineWidth', 1)
grid on
xlabel('Time ($sec.$)','Interpreter', 'latex');
ylabel('Displacement ($m$)','Interpreter', 'latex');
title('Displacement vs.time')

ax6 = subplot(5,2,9:10);
plot(f,P1, 'LineWidth', 1)
grid on
title('Frequency Spectrum of Acceleration')
xlabel('f(Hz)')
ylabel('|P1(f)|')