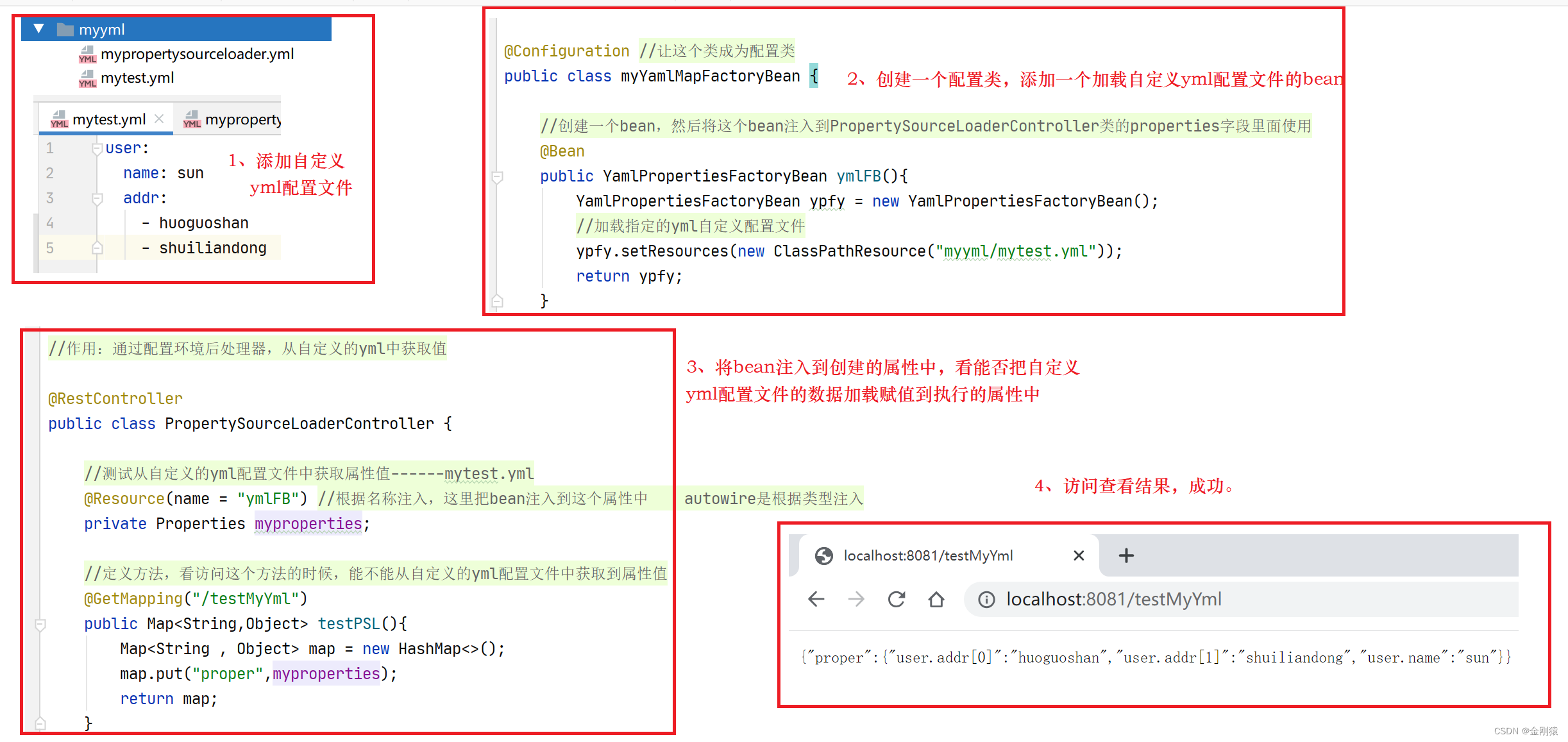
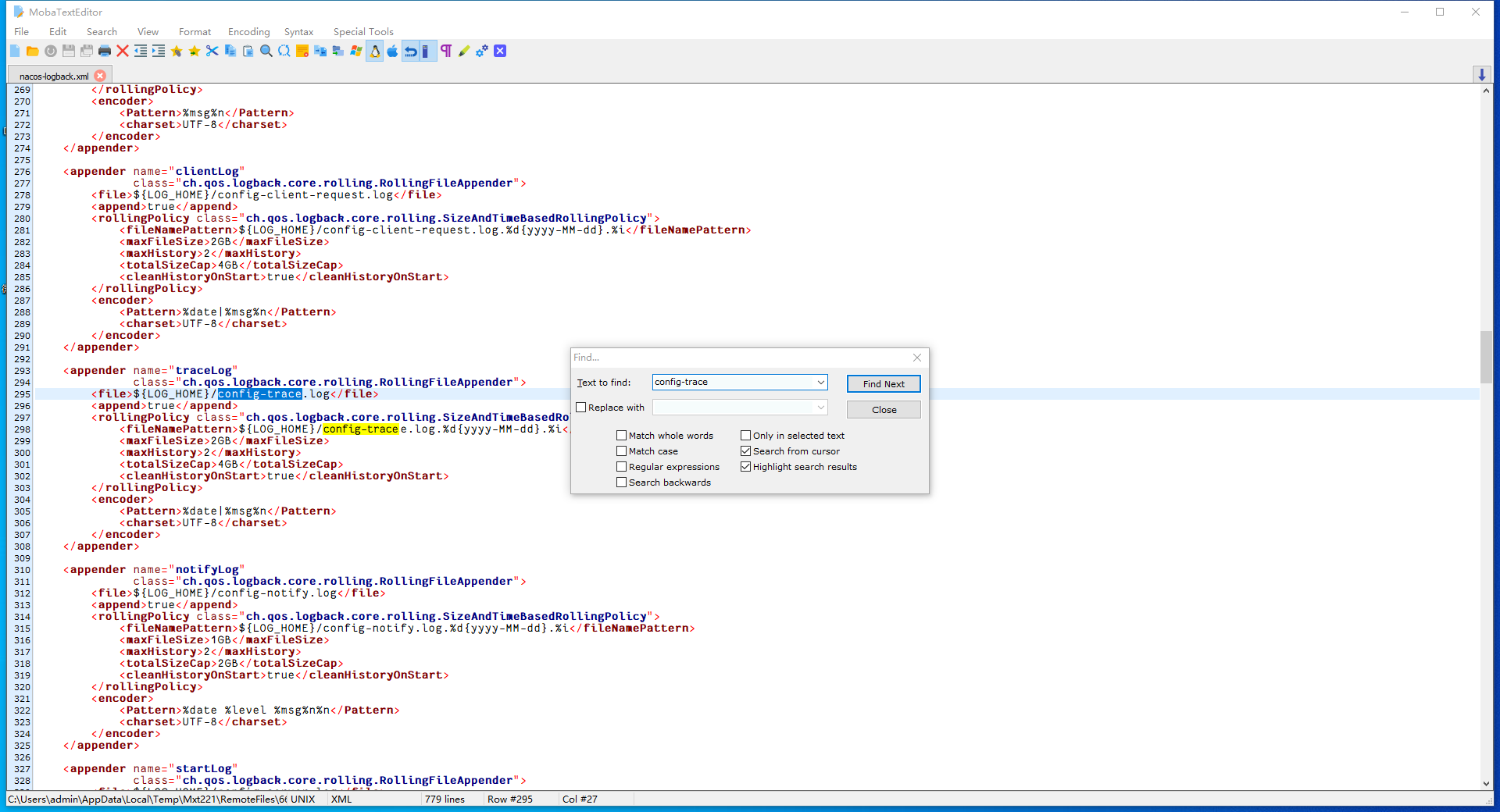
背景
首先是借鉴Corner Net 表述了一下基于Anchor方法的不足:
- anchor的大小/比例需要人工来确认
- anchor并没有完全和gt的bbox对齐,不利于分类任务。
但是CornerNet也有自己的缺点
- CornerNet 只预测了top-left和bottom-right 两个点,并没有关注整体的信息,因此缺少一些全局的信息
- 上述的点导致它对边界过于敏感,经常会预测一些错误的bbox。
为了解决该问题,作者提出了Triplet的关键点预测。他follow了top-left和bottom-right的预测,此外增加了中心点的预测。
具体来说,为了使得中心点的预测更加准确,作者提出了Center Pooling的层用来在水平和垂直两个维度进行特征的聚合。使得每个位置的点都可以尽可能的感知到全局的信息。
此外,作者还提出了cascade corner pooling layer来取代原有的corner pooling layer。
作者也从指标的角度量化了上面提到的CornerNet比较容易出现False Positive的情况,如下图所示。作者展示了在不同IoU阈值下 False Discovery Rate。注意这里为什么没有用mAP,mAP是否有缺点?
- 框的增加,在recall不变的情况下,precision的下降不会导致mAP的下降。=>因此需要关注PR曲线的分数
- mAP是分类别计算的,每个类别都是按照分数排序来计算的,说明每个类别的分数阈值可能会不同,不能用同一个阈值在适应不同的类别。

方法
CenterNet的网络结构如下图所示

整个网络的推理流程如下所示:
- 选择top-k个中心点根据他们的分数
- 根据对应的offset将其还原到对应的输入图像中
- 根据tl-br构成的bbox,判断每个bbox内部的中心区域是否包括上述的中心点。
3.1 N个tl的点和N个br 的点,组合形成N*N个bbox
3.2 如果tl和br的embedding相似度小于阈值,则将对应的bbox剔除,否则保留。 - 如果中心点在bbox中,则用三者分数(tl、br和center)的平均来表示bbox的置信度。
那么这里涉及到一个问题,那就是如何计算每个bbox的中心区域。作者这里认为大的bbox应该使用小的中心区域,避免precision过低。小的bbox应该使用大的中心区域,避免recall过低。因此这里作者提出了scale-aware的中心区域计算方法,详情如下所示,其中针对大物体,n选择5,针对小物体,n选择3。


上述介绍了推理的整体流程,那么我们在从内部逐步解析一下关键的结构,我们分别从center pooling、cascade corner pooling和loss来进行介绍。
center pooling
center pooling的示意图如下图所示。具体来说就是针对每个位置,我们计算其水平和垂直方向的max response,然后想加得到该位置的表征,我们认为这样的表征是包括了全局信息。简化版本的计算如下所示,其中 f , f 3 ∈ R H × W × C f,f_3 \in R^{H \times W \times C} f,f3∈RH×W×C
f1 = np.max(f, axis=0)
f2 = np.max(f, axis=1)
f3 = f1[None, :, :] + f2[:, None, :]

cascaded corner pooling
示意图如下所示

loss
损失函数的定义如下所示。整体上分为三大部分。
-
L d e t c o 、 L d e t c e L_{det}^{co}、L_{det}^{ce} Ldetco、Ldetce表示的corner 和 center两个heatmap组成的loss,这里采用的是focal loss。
-
L p u l l c o 、 L p u s h c o L_{pull}^{co}、L_{push}^{co} Lpullco、Lpushco是让属于同一个物体的corner embedding尽可能相似,属于不同物体的embedding尽可能远离。
-
L o f f c o 、 L o f f c e L_{off}^{co}、L_{off}^{ce} Loffco、Loffce 表示预测corner 和 center在原图上的offset,这里采用的是l1-loss。
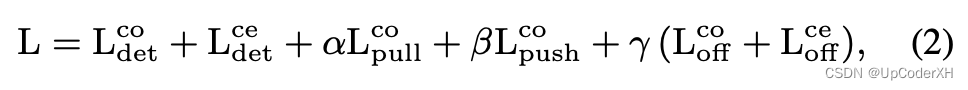
-
QA1:GT是如何计算的?








![[NOIP2007 普及组] 纪念品分组](https://img-blog.csdnimg.cn/4f8c98d0600d427aade5f3e49f2f4393.png)