小结

k近邻算法（knn）

定义

如果一个样本在特征空间中的k个最相似(即特征空间中最邻近)的样本中的大多数属于某一个类别，则该样本也属于这个类别。

算法流程

1）计算已知类别数据集中的点与当前点之间的距离

2）按距离递增次序排序

3）选取与当前点距离最小的k个点

4）统计前k个点所在的类别出现的频率

5）返回前k个点出现频率最高的类别作为当前点的预测分类

距离度量

1 欧式距离(Euclidean Distance)：
2 曼哈顿距离(Manhattan Distance)：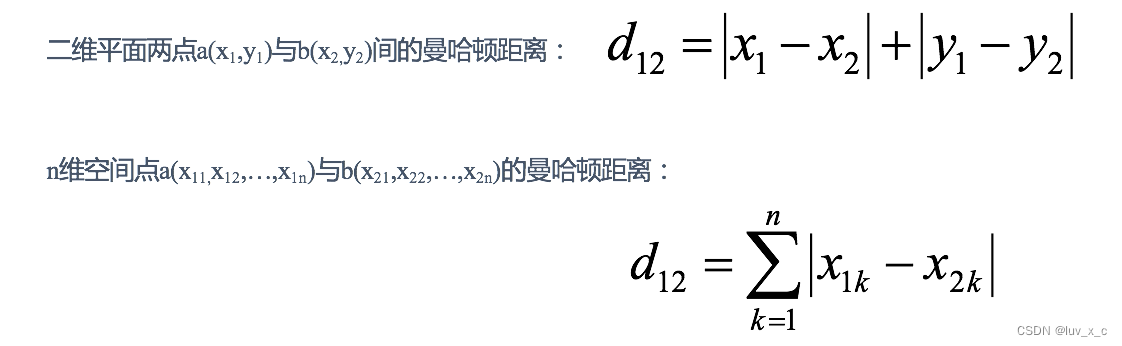
3 标准化欧氏距离 (Standardized EuclideanDistance)：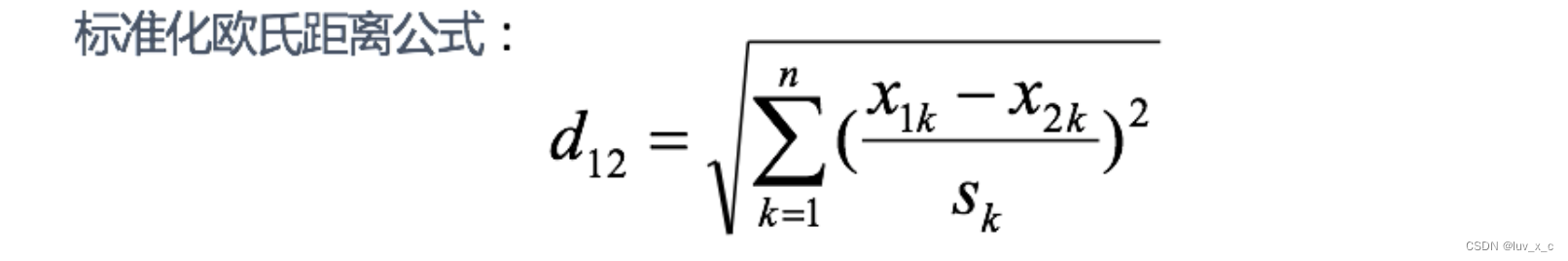

k值的选择

K值过小：容易受到异常点的影响 容易过拟合
k值过大：受到样本均衡的问题 容易欠拟合

总结

k近邻算法总结
优点：

• 简单有效
• 重新训练的代价低
• 适合类域交叉样本
  KNN方法主要靠周围有限的邻近的样本,而不是靠判别类域的方法来确定所属类别的，因此对于类域的交叉或重叠较多的待分样本集来说，KNN方法较其他方法更为适合。
• 适合大样本自动分类
  该算法比较适用于样本容量比较大的类域的自动分类，而那些样本容量较小的类域采用这种算法比较容易产生误分。

缺点：

• 惰性学习
  KNN算法是懒散学习方法（lazy learning,基本上不学习），一些积极学习的算法要快很多
• 类别评分不是规格化
  不像一些通过概率评分的分类
• 输出可解释性不强
  例如决策树的输出可解释性就较强
  对不均衡的样本不擅长
  当样本不平衡时，如一个类的样本容量很大，而其他类样本容量很小时，有可能导致当输入一个新样本时，该样本的K个邻居中大容量类的样本占多数。该算法只计算“最近的”邻居样本，某一类的样本数量很大，那么或者这类样本并不接近目标样本，或者这类样本很靠近目标样本。无论怎样，数量并不能影响运行结果。可以采用权值的方法（和该样本距离小的邻居权值大）来改进。
• 计算量较大
  目前常用的解决方法是事先对已知样本点进行剪辑，事先去除对分类作用不大的样本。

聚类

定义

一种典型的无监督学习算法，主要用于将相似的样本自动归到一个类别中。

在聚类算法中根据样本之间的相似性，将样本划分到不同的类别中，对于不同的相似度计算方法，会得到不同的聚类结果，常用的相似度计算方法有欧式距离法。

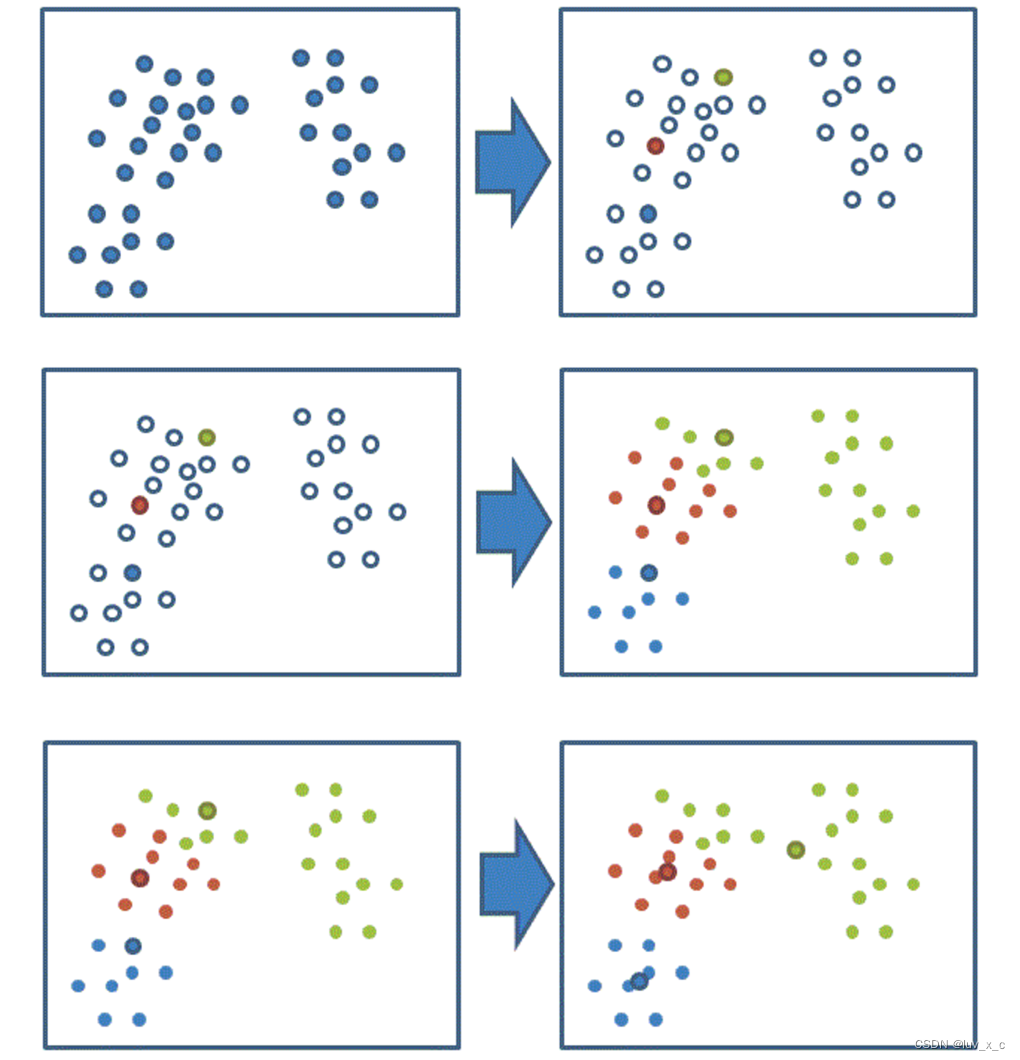
k-means聚类步骤

1、随机设置K个特征空间内的点作为初始的聚类中心
2、对于其他每个点计算到K个中心的距离，未知的点选择最近的一个聚类中心点作为标记类别
3、接着对着标记的聚类中心之后，重新计算出每个聚类的新中心点（平均值）
4、如果计算得出的新中心点与原中心点一样（质心不再移动），那么结束，否则重新进行第二步过程

k-means算法小结

优点：

​ 1.原理简单（靠近中心点），实现容易

​ 2.聚类效果中上（依赖K的选择）

​ 3.空间复杂度o(N)，时间复杂度o(IKN)

N为样本点个数，K为中心点个数，I为迭代次数
缺点：

​ 1.对离群点，噪声敏感 （中心点易偏移）

​ 2.很难发现大小差别很大的簇及进行增量计算

​ 3.结果不一定是全局最优，只能保证局部最优（与K的个数及初值选取有关）