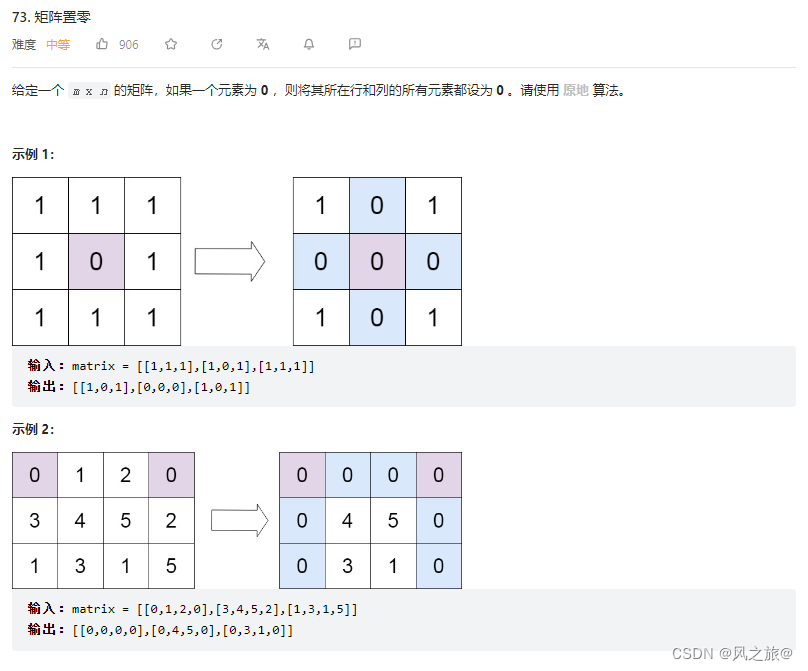
题目链接：力扣

解题思路：

方法一：比较容易想到的方向，使用两个数组row和col保存有0的行或者列，然后将有0的那一行或那一列的所有元素都设置为0

AC代码

class Solution {public void setZeroes(int[][] matrix) {int x = 0;boolean[] row  = new boolean[matrix.length];boolean[] col = new boolean[matrix[0].length];for (int i = 0;i<matrix.length;i++){for (int j =0;j<matrix[0].length;j++){if (matrix[i][j]==0){row[i]=true;col[j]=true;}}}for (int i = 0;i<matrix.length;i++){for (int j =0;j<matrix[0].length;j++){if (row[i]||col[j]){matrix[i][j]=0;}}}}
}

 

这种方式的时间复杂度为O(mn) ，空间复杂度为O(m+n)

解法二：空间复杂度为O(1)

 可以使用矩阵的第一行和第一列来记录当前行或当前列是否需要更新

算法步骤：

1. 遍历整个矩阵，如果某个元素为0，就将该元素所在的行和列的首元素标记为0，表示该行和列需要置0。但是需要使用两个额外的变量来记录原来的第一行和第一列是否有0。
2. 更新时从第二行和第二列开始更新，如果某行或某列的首元素为0，说明该行或该列需要置0，
3. 最后判断第一行和第一列是否需要置0

AC代码

class Solution {public static void setZeroes(int[][] matrix) {boolean firstRow = false;boolean firstCol = false;for (int i = 0; i < matrix.length; i++) {for (int j = 0; j < matrix[0].length; j++) {if (matrix[i][j] == 0) {matrix[i][0] = 0;matrix[0][j] = 0;if (i == 0) {firstRow = true;}if (j == 0) {firstCol = true;}}}}for (int i = 1; i < matrix.length; i++) {for (int j = 1; j < matrix[0].length; j++) {if (matrix[i][0] == 0 || matrix[0][j] == 0) {matrix[i][j] = 0;}}}if (firstRow) {Arrays.fill(matrix[0], 0);}if (firstCol) {for (int i = 0; i < matrix.length; i++) {matrix[i][0] = 0;}}}
}