文章目录
- 连续波光纤耦合激光器
- 工作原理
- 主要特点
- 应用领域
- 设计考虑因素
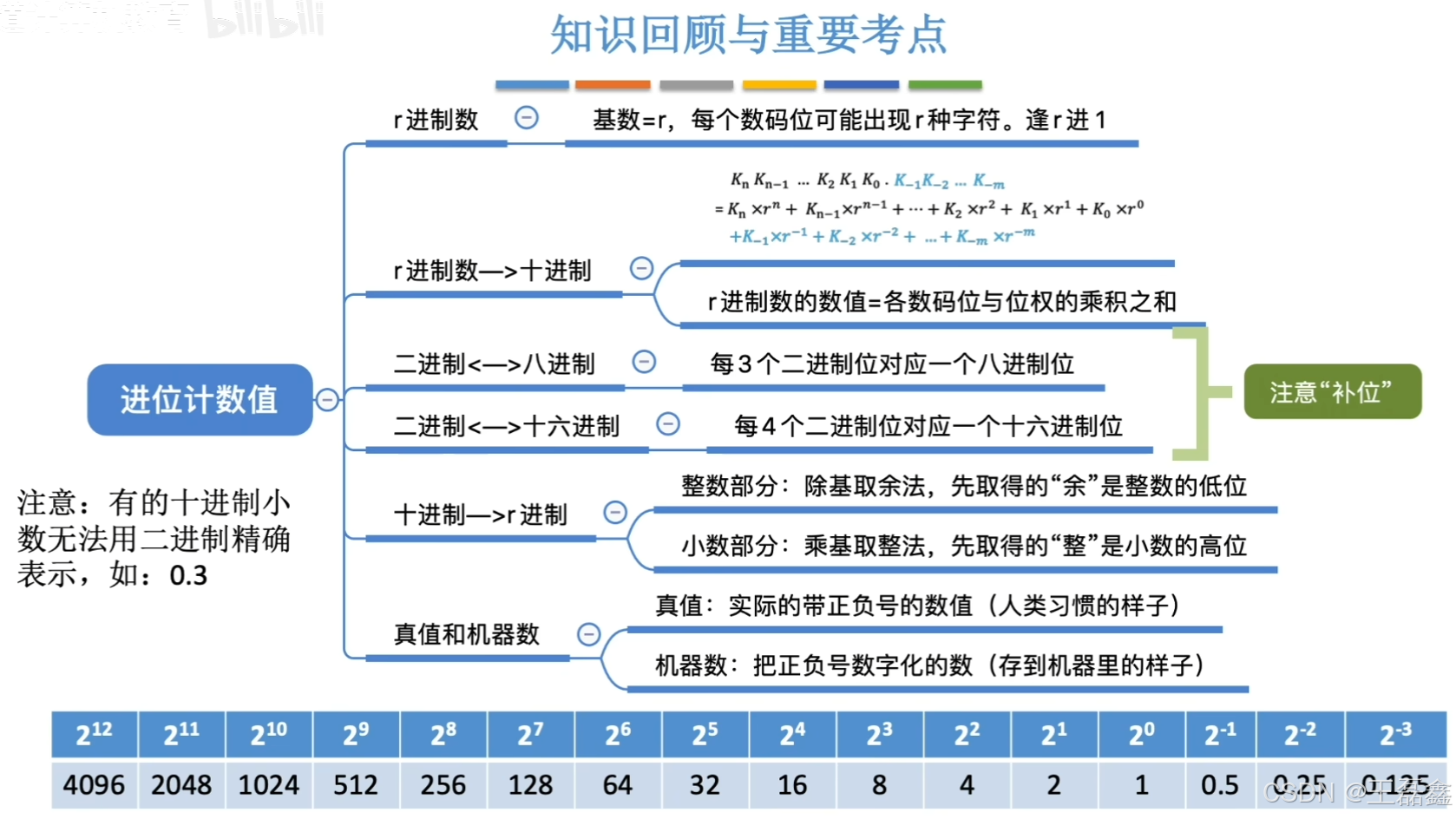
- 数值孔径(Numerical Aperture,简称NA)
- 数值孔径的定义
- 数值孔径的意义
- 数值孔径的计算示例
- 数值孔径与光纤
- 四象限探测器检测目标方法
- 四象限划分
- 检测目标的步骤
- 1. 数据采集
- 2. 坐标转换
- 3. 四象限判断
- 4. 目标位置识别
- 5. 目标跟踪与响应
- 代码示例(基于传感器数据)
- Wiener 滤波
- 维纳滤波的基本原理
- 1. 目标函数:最小化均方误差(MSE)
- 2. 频域表示
- 图像去噪
- 维纳滤波的优势与限制
- 优势:
- 限制:
- Wiener 滤波的实现
- 代码说明:
- LM2596S DC-DC 降压电源
- LM2596S 的特点:
- LM2596S模块的元器件
连续波光纤耦合激光器
连续波光纤耦合激光器(CW Fiber-coupled Laser)是一种利用光纤传输激光输出的激光器。其特点是输出的激光为连续波(Continuous Wave,CW)形式,即激光的输出功率是稳定和持续的,没有明显的脉冲特征。这种激光器通常用于精密加工、传感、医疗等多个领域,具有高稳定性和良好的光束质量。
工作原理
连续波光纤耦合激光器的基本原理是通过光纤将激光从激光源传输到目标位置。光纤耦合技术使得激光器具有更高的输出效率、光束质量和方向性。其工作过程大致可以分为以下几个步骤:
-
激光源:激光器本身通常是半导体激光器、固体激光器或气体激光器等。激光源通过电流或光源激发介质,使其发射出特定波长的激光。
-
光纤耦合:激光通过耦合系统(例如透镜、反射镜等)导入光纤中。耦合的过程需要确保光纤能够有效地接收到激光源的输出,并将光传输到输出端。
-
光纤传输:光纤作为光的传输通道,传输过程中几乎没有能量损失,因此能够保证激光输出的稳定性。通过光纤,激光可以被精确地传输到需要的位置。
-
输出激光:最终,激光通过光纤输出端口传递到目标区域。由于光纤的特殊结构,激光的输出通常具有较小的光斑和较高的光束质量。
主要特点
-
高稳定性:连续波光纤耦合激光器能够提供稳定的输出功率,适合精密控制和长时间运行。
-
良好的光束质量:光纤传输过程中能够保持较高的光束质量,适合对光束质量有要求的应用。
-
紧凑性:光纤耦合激光器的结构相对紧凑,易于集成进各种设备中。
-
高效率:通过光纤传输,激光损耗较低,系统整体效率较高。
-
较强的抗干扰能力:光纤本身对电磁干扰不敏感,因此能够保证在复杂环境下正常工作。
应用领域
-
精密加工:在材料加工、激光切割、激光焊接等领域,连续波光纤耦合激光器可以提供高精度、高功率的激光输出,广泛应用于金属、陶瓷等材料的加工。
-
激光扫描与传感:在激光扫描、三维成像、激光雷达(LiDAR)等应用中,光纤耦合激光器提供稳定的激光输出,用于高精度测量。
-
医疗领域:在激光治疗、激光手术等医疗领域,连续波激光器被用于组织切割、消融等操作,具有较高的精准性和可控性。
-
通信与研究:在光通信领域,光纤耦合激光器被广泛用于信号传输和实验研究。
设计考虑因素
在设计连续波光纤耦合激光器时,需要考虑以下几个因素:
-
光纤匹配:选择适合的光纤和耦合方式,确保激光器的输出能够有效耦合入光纤。
-
功率控制:设计适当的驱动电路和温控系统,确保激光器输出的功率稳定且可调。
-
热管理:激光器工作时会产生大量热量,良好的热管理系统能够防止激光器过热,确保长时间稳定运行。
-
波长选择:根据应用需求选择适当的激光波长,光纤的传输性能和耦合效率也会随波长的不同而有所变化。
-
光束质量:确保激光器的输出光束具有良好的质量,以适应精密加工或高精度测量的需求。
数值孔径(Numerical Aperture,简称NA)
数值孔径(NA)是描述光学系统,特别是显微镜、光纤等光学设备的光学性能的重要参数。它表征了光学系统能够接收或发射光的能力,即系统的光学聚焦能力与分辨率的关系。
数值孔径的定义
数值孔径是由光学系统的物镜(或光纤的核心)与透镜的光学特性共同决定的,它是一个无单位的数值,定义如下:
N A = n sin θ NA = n \sin \theta NA=nsinθ
其中:
- n n n 是介质的折射率,通常是物镜与物体之间的介质(如空气、水、油等)的折射率。
- θ \theta θ 是物镜半角(或入射光束的最大半角),即光线从物镜的中心轴到边缘所形成的角度。
数值孔径的意义
-
光学系统的聚焦能力:数值孔径越大,光学系统的聚焦能力越强,能够集中更多的光线,形成更小的焦点。因此,NA越大,系统的分辨率通常也会更高。
-
光纤的传输能力:在光纤通信中,NA反映了光纤核心能够接受的光线角度范围。较大的NA表示光纤可以接受更多不同角度的光线,传输效率和带宽也更高。
-
分辨率与物镜性能:数值孔径与分辨率相关。分辨率 R R R 与NA之间的关系为:
R = λ 2 × N A R = \frac{\lambda}{2 \times NA} R=2×NAλ
其中, λ \lambda λ 是使用的光的波长。可以看到,数值孔径越大,分辨率越高。
数值孔径的计算示例
假设我们有一个在空气中工作的物镜,折射率 n = 1.0 n = 1.0 n=1.0,入射角度为 3 0 ∘ 30^\circ 30∘,那么数值孔径NA为:
N A = 1.0 × sin ( 3 0 ∘ ) = 1.0 × 0.5 = 0.5 NA = 1.0 \times \sin(30^\circ) = 1.0 \times 0.5 = 0.5 NA=1.0×sin(30∘)=1.0×0.5=0.5
若这个系统使用的是水作为介质,其折射率通常为 n = 1.33 n = 1.33 n=1.33,那么:
N A = 1.33 × sin ( 3 0 ∘ ) = 1.33 × 0.5 = 0.665 NA = 1.33 \times \sin(30^\circ) = 1.33 \times 0.5 = 0.665 NA=1.33×sin(30∘)=1.33×0.5=0.665
可以看出,水介质下的数值孔径比空气中的数值孔径更大,表明水介质下的物镜能够聚焦更多的光线,从而提供更高的分辨率。
数值孔径与光纤
在光纤中,数值孔径的作用是决定光纤的接受角度(或模式)的能力。光纤的NA越大,可以接收到更多不同方向的光线,从而能够支持更多的传播模式,这对于多模光纤尤其重要。
对于光纤,数值孔径也由其核心和包层的折射率差异决定,通常使用如下公式计算:
N A = n 1 2 − n 2 2 NA = \sqrt{n_1^2 - n_2^2} NA=n12−n22
其中:
- n 1 n_1 n1 是光纤核心的折射率。
- n 2 n_2 n2 是光纤包层的折射率。
四象限探测器检测目标方法
四象限探测器(Quadrant Detector),又是一个唬人的名词,本质上就是看物体运动到从哪个象限到哪个象限,判断是哪个方向。
四象限探测器通过将检测区域划分为四个象限(上下左右四个部分),根据目标的分布位置来判断目标是否存在以及其大致位置。
四象限划分
我们通常将平面坐标系的原点 ( 0 , 0 ) (0, 0) (0,0) 放置在检测区域的中心,基于此将区域划分为四个象限,分别为:
- 第一象限:右上, x > 0 , y > 0 x > 0, y > 0 x>0,y>0
- 第二象限:左上, x < 0 , y > 0 x < 0, y > 0 x<0,y>0
- 第三象限:左下, x < 0 , y < 0 x < 0, y < 0 x<0,y<0
- 第四象限:右下, x > 0 , y < 0 x > 0, y < 0 x>0,y<0
通过这种划分,探测器可以分别检测目标是否处于某个象限,并根据这些信息来判断目标的方位和移动方向。
检测目标的步骤
1. 数据采集
首先,通过传感器(如红外传感器、激光雷达、相机等)采集目标的位置信息。这些传感器可以通过测量与目标之间的距离、角度或者其他相关特征来获取目标的位置数据。
- 如果使用图像处理方法,可以通过摄像头获取目标的图像信息。
- 如果使用激光雷达,可以通过点云数据或反射信号获得目标在空间中的坐标。
2. 坐标转换
将目标的坐标数据转换为平面坐标系中的 x , y x, y x,y 坐标。对于激光雷达或其他传感器采集的数据,可能需要根据传感器的角度和距离计算出目标的实际位置。
例如,假设有一个距离 d d d 和角度 θ \theta θ,则可以通过极坐标转直角坐标来得到目标的 x , y x, y x,y 坐标:
x = d ⋅ cos ( θ ) x = d \cdot \cos(\theta) x=d⋅cos(θ)
y = d ⋅ sin ( θ ) y = d \cdot \sin(\theta) y=d⋅sin(θ)
3. 四象限判断
根据得到的 x , y x, y x,y 坐标,判断目标所在的象限:
- 第一象限: x > 0 , y > 0 x > 0, y > 0 x>0,y>0
- 第二象限: x < 0 , y > 0 x < 0, y > 0 x<0,y>0
- 第三象限: x < 0 , y < 0 x < 0, y < 0 x<0,y<0
- 第四象限: x > 0 , y < 0 x > 0, y < 0 x>0,y<0
如果目标的坐标满足某个象限的条件,说明目标位于该象限内。
4. 目标位置识别
通过四象限的划分,可以判断目标的相对位置。如果目标穿越某一象限的边界,探测器可以进一步识别目标的移动方向。
例如,若目标从第一象限移动到第二象限,则说明目标向左移动。如果目标从第一象限进入第四象限,则说明目标向下移动。
5. 目标跟踪与响应
若探测器用于实时跟踪目标,可以通过连续采集和计算目标的位置变化来持续判断其位置和方向,进行相应的操作。对于一些自动化系统,可以根据目标所在的象限来做出相应的决策,如改变机器人方向、触发某些操作等。
代码示例(基于传感器数据)
假设我们已经获取了目标的 x x x 和 y y y 坐标,以下是一个简单的C语言代码示例来判断目标是否位于四象限中的某一象限:
#include <stdio.h>// 判断目标所在的象限
void detectQuadrant(float x, float y) {if (x > 0 && y > 0) {printf("目标在第一象限\n");} else if (x < 0 && y > 0) {printf("目标在第二象限\n");} else if (x < 0 && y < 0) {printf("目标在第三象限\n");} else if (x > 0 && y < 0) {printf("目标在第四象限\n");} else if (x == 0 && y != 0) {printf("目标在Y轴上\n");} else if (y == 0 && x != 0) {printf("目标在X轴上\n");} else {printf("目标在原点\n");}
}int main() {float x, y;// 输入目标坐标printf("请输入目标的X坐标:");scanf("%f", &x);printf("请输入目标的Y坐标:");scanf("%f", &y);// 判断目标所在的象限detectQuadrant(x, y);return 0;
}
Wiener 滤波
Wiener 滤波(维纳滤波)是一种基于统计学的滤波方法,广泛应用于信号处理和图像处理等领域,旨在通过最小化均方误差(MSE)来估计信号或图像中的噪声并进行去噪处理。Wiener 滤波器的核心思想是根据信号和噪声的统计特性,构建一个最佳的滤波器,从而达到降噪的目的。
维纳滤波的基本原理
Wiener 滤波的目标是通过某种方式估计原始信号 x ( n ) x(n) x(n)(或图像中的清晰图像)并消除其中的噪声。给定噪声信号 y ( n ) y(n) y(n),维纳滤波的目标是根据已知的信号与噪声的统计特性,构建一个最优的滤波器 H ( f ) H(f) H(f),使得输出信号 z ( n ) z(n) z(n) 尽可能接近原始信号 x ( n ) x(n) x(n),并且最小化输出信号与原始信号之间的均方误差。
1. 目标函数:最小化均方误差(MSE)
Wiener 滤波的核心是最小化均方误差(MSE),即:
J = E [ ( x ( n ) − z ( n ) ) 2 ] J = E[(x(n) - z(n))^2] J=E[(x(n)−z(n))2]
其中, x ( n ) x(n) x(n) 是原始信号, z ( n ) z(n) z(n) 是滤波后的信号, E [ ⋅ ] E[\cdot] E[⋅] 表示期望值操作。Wiener 滤波器的目标是选择一个滤波器 H ( f ) H(f) H(f),使得该误差最小化。
2. 频域表示
在频域中,Wiener 滤波器的理想形式为:
H ( f ) = S x ( f ) S x ( f ) + S n ( f ) H(f) = \frac{S_x(f)}{S_x(f) + S_n(f)} H(f)=Sx(f)+Sn(f)Sx(f)
其中, S x ( f ) S_x(f) Sx(f) 是原始信号的功率谱密度, S n ( f ) S_n(f) Sn(f) 是噪声的功率谱密度。该公式的含义是,Wiener 滤波器的增益在信号强时较大,在噪声较强时较小,从而能够有效抑制噪声。
图像去噪
在图像处理中,Wiener 滤波常用于去除图像中的高斯噪声。假设原始图像 f ( x , y ) f(x, y) f(x,y) 和噪声图像 g ( x , y ) g(x, y) g(x,y) 之间的关系如下:
g ( x , y ) = f ( x , y ) + n ( x , y ) g(x, y) = f(x, y) + n(x, y) g(x,y)=f(x,y)+n(x,y)
其中, n ( x , y ) n(x, y) n(x,y) 是添加到图像中的噪声。Wiener 滤波器通过以下公式对图像进行去噪:
f ^ ( x , y ) = ∑ u , v h ( u , v ) g ( x − u , y − v ) \hat{f}(x, y) = \sum_{u, v} h(u, v) g(x-u, y-v) f^(x,y)=u,v∑h(u,v)g(x−u,y−v)
其中, h ( u , v ) h(u, v) h(u,v) 是 Wiener 滤波器核函数, f ^ ( x , y ) \hat{f}(x, y) f^(x,y) 是滤波后的图像。
维纳滤波的优势与限制
优势:
- 最小化均方误差:Wiener 滤波通过统计学方法,能够找到最优的滤波器,从而使得去噪效果最好,能最大限度地保留信号。
- 自适应性:Wiener 滤波器能够根据信号和噪声的统计特性自动调整滤波参数,具有较强的自适应性。
- 广泛应用:适用于各种信号和图像去噪任务,特别是对高斯噪声有良好的效果。
限制:
- 需要先验知识:Wiener 滤波需要了解信号和噪声的功率谱密度。若噪声模型不准确,可能导致滤波效果不佳。
- 计算复杂度较高:计算信号和噪声的功率谱密度以及实现频域滤波可能需要较高的计算资源。
- 对非高斯噪声的效果不佳:Wiener 滤波主要适用于高斯噪声,对于其他类型的噪声(如椒盐噪声),效果可能不如预期。
Wiener 滤波的实现
以下是一个基于Python的Wiener滤波实现代码示例,用于图像去噪:
import numpy as np
import cv2
from scipy.signal import convolve2ddef wiener_filter(img, noise_var, signal_var):"""实现Wiener滤波器用于图像去噪:param img: 输入的噪声图像:param noise_var: 噪声的方差:param signal_var: 信号的方差:return: 去噪后的图像"""# 获取图像的大小rows, cols = img.shape # 获取图像的行数和列数# 对输入图像进行二维快速傅里叶变换(FFT)fft_img = np.fft.fft2(img) # 将图像转换到频域fft_img_conj = np.conj(fft_img) # 计算图像的共轭复数(对于频域滤波,通常使用共轭)# 计算信号的功率谱密度(Power Spectral Density,PSD)signal_psd = np.abs(fft_img) ** 2 / (rows * cols) # 图像的功率谱(幅度的平方),并归一化到单位面积# 计算噪声的功率谱密度,噪声功率谱假设是一个常数noise_psd = noise_var * np.ones_like(signal_psd) # 噪声的功率谱密度,假设噪声方差为常数# 计算Wiener滤波器的频域传递函数H(f)H = signal_psd / (signal_psd + noise_psd) # Wiener滤波器的增益函数,利用信号和噪声的功率谱计算# 应用Wiener滤波器(在频域上)wiener_filtered = np.fft.ifft2(fft_img_conj * H) # 在频域内进行滤波,进行反傅里叶变换得到去噪后的图像# 返回滤波后的图像的绝对值(因为fft的结果可能是复数)return np.abs(wiener_filtered)# 读取含噪声的图像
noisy_image = cv2.imread('noisy_image.png', cv2.IMREAD_GRAYSCALE) # 读取灰度图像# 假设信号和噪声的方差
noise_variance = 0.1 # 假设噪声的方差为0.1
signal_variance = 0.9 # 假设信号的方差为0.9# 使用Wiener滤波进行去噪
denoised_image = wiener_filter(noisy_image, noise_variance, signal_variance) # 对噪声图像进行去噪# 显示原始图像和去噪后的图像
cv2.imshow('Original', noisy_image) # 显示原始噪声图像
cv2.imshow('Denoised', denoised_image) # 显示去噪后的图像
cv2.waitKey(0) # 等待用户按键
cv2.destroyAllWindows() # 关闭所有OpenCV窗口代码说明:
- FFT和频域操作:在代码中,我们将图像转换到频域,通过傅里叶变换计算信号的功率谱和噪声的功率谱。
- Wiener滤波器的实现:Wiener滤波器在频域中通过信号和噪声的功率谱来计算频域滤波函数 H ( f ) H(f) H(f),然后对图像进行滤波。
- 去噪图像显示:处理后的图像通过
imshow函数显示,便于直观比较。
LM2596S DC-DC降压电源模块是一款非常常见的开关电源降压转换器(Buck Converter),广泛应用于各种电子设备的电源设计中。它可以将较高的输入电压转换为较低的输出电压,且具有高效、稳定的特性。以下是对LM2596S模块的一些详细介绍。
LM2596S DC-DC 降压电源
LM2596S是由Texas Instruments (德州仪器) 提供的一款集成开关调节器芯片。该芯片采用了降压转换方式,即高电压输入经过调节后输出较低电压的过程。LM2596S模块通常集成在一块小型电路板上,具有良好的散热设计和多种输出电压选择,适合嵌入到各种项目中。
LM2596S 的特点:
-
宽输入电压范围:
LM2596S的输入电压范围为 4V到40V。这使得它可以从多种不同的电源(如12V电池、电源适配器等)中获取能量。 -
输出电压可调:
LM2596S的输出电压范围为 1.25V到37V,通过电位器调节输出电压。也有一些模块提供固定输出电压版本(如5V、12V、15V等)。 -
高效率:
LM2596S作为开关电源,具有相对较高的转换效率(通常高于80%),比传统线性电压调节器具有更低的功耗和更少的热量产生。 -
输出电流:
LM2596S可以提供最大 2A 的输出电流,这对于大多数低功耗应用来说足够。 -
内置过热、过载和短路保护:
LM2596S具有过热保护、过电流保护和短路保护功能,在异常情况下可以自动关闭以保护电路。 -
简单的外部组件:
只需要少数几个外部元件,如电感、电容、二极管等,就可以实现高效的电压转换。
LM2596S模块的元器件
- 输入电压 (Vin):供电输入端,通常为12V或更高的电压。
- 电感 (L):用于滤波和能量存储,帮助降低输出电压的噪声。
- 二极管 (D):通常为肖特基二极管,用于防止反向电流。
- 电容 ©:用于平滑输出电压,减少电压波动。