数据挖掘全流程解析
数据指标选择
在这一阶段,使用直方图和柱状图的方式对数据进行分析,观察什么数据属性对于因变量会产生更加明显的结果。
如何绘制直方图和条形统计图
数据清洗
观察数据是否存在数据缺失或者离群点的情况。
数据异常的两种情况 :
1、不完整(缺少属性值)
2、含有噪音数据(错误或者离群)
缺失数据的处理方法:
1、忽略元组(当每个属性的缺失值比例比较大时,效果非常差,直接删除处理)
2、手动填写缺失值(工作量会比较大)
3、自动填写(使用属性的缺失值进行填充,仅对于连续性数值类型的数值适用),假如数据是离散标签类型数据,则使用相应的众数进行填充。
噪音数据的处理方法(使用3sigma原则或者箱线图发现离群点,再进行删除操作):
1、正态分布的3sigma原则

2、箱线图进行监测,发现离群数据,进一步删除离群点(箱线图又称为五分位图)其中含有离群点、最大值、最小值、四分之一位数、四分之三位数、中位数。
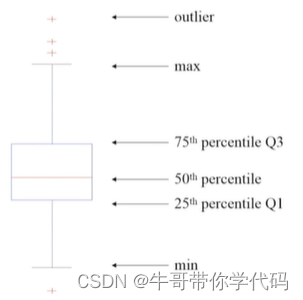
上述图中的最小值和最大值不一定会指的是数据中的真正的最小值和最大值,因为数据中真正的最小值和最大值可能是离群点。怎样求最小值和最大值捏?使用下面公式进行判断:
我们计四分之一位数为Q1,四分之三位数为Q3。
首先计算四分之一极差:
四分之一极差 IQR=Q3-Q1
最大值=Q3+1.5*极差
最小值=Q1-1.5*极差
离群点:通常情况下的一个值高于1.5倍的极差或者低于1.5倍的极差。.
使用下面代码即可绘制箱线图
import pandas as pd
import numpy as np
import matplotlib.pyplot as pl
from sklearn.impute import Simplelmputer
data url = "train.csv"
df= pd.read_csv(data_url)
imp = SimpleImputer(missing_values = np.nan, strategy = 'mean')
imp.fit(df.iloc[:,5:6))
pl.boxplot(imp.transform(df.iloc[:,5:6])
pl.xlabel('data')
pl.show()
数据转换
数据中既有字符串也有数值、且数值量纲不统一。
需要统一化:字符数值统一化
需要规范化:统一量纲
离散数据特征的二进制编码
对于标称类(无序)离散数据连续化特征构造通常采用二进制编码方法
对于序数类离散数据连续化特征构造可以直接使用[0,m-1]的整数
数据规范化
最小最大规范化: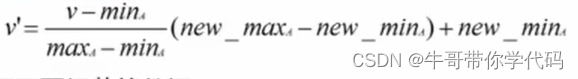
z-分数规范化:

小数定标:移动属性A的小数点位置(移动位数依赖于属性A的最大值)v'=v/10^j , j为使Max(|v'|)<1的最小整数
二进制编码方式
(1)代码实现sklearn中的OneHotEncoder(独热编码)->二进制中只允许一位为1
import pandas as pd
from sklearn import preprocessing
data_url = "train.csv"
df= pd.read_esv(data_url)
X = df.iloc[:,4:5]
enc = preprocessing.OneHotEncoder()
y = enc.fit_transform(X).toarray()
print(y) 
上述代码是将序数类型的数据编码成[0,m-1]范围内的整数
哑编码(允许多个位为一)
哑编码需要更少的二进制编码,独热编码需要更多的二进制编码(因为独热编码只允许一个二进制为1,所以没有哑编码的表现力那么强,需要更多的二进制编码)。
import pandas as pd
data_url = "train.csv"
df = pd.read_csv(data_url)
X = df.iloc[:,11:12]
y = pd.get_dummies(X,drop_first=True)
print(y)drop_first=True 为哑编码
drop_first=False 为独热编码
上面的代码既可以做独热编码也可以做哑编码
两种规范化函数
最小最大规范化函数
from sklearn import preprocessing
data_url = "train.csv"
df= pd.read_csv(data_url)
imp = Simplelmputer(missing_values = np.nan, strategy = 'mean')
imp.fit(df.iloc[:,5:6])
X = imp.transform(df.iloc[:,5:6])
min_max_scaler = preprocessing.MinMaxScaler()
X_train_minmax = min_max_scaler.fit_transform(X)
print(X_train_minmax)当获得的数据属于数值类型数据时,可以在建模之前使用最小最大规范化函数对量纲作一个统一。同时,我们也可以使用下面的方法进行量纲的统一。
z得分规范化
import pandas as pd
import numpy as np
from sklearn.impute import Simplelmputer
from sklearn import preprocessing
data_url = "train.csv"
df= pd.read_csv(data_url)
imp = Simplelmputer(missing_values = np.nan, strategy = 'mean')
imp.fit(df.iloc[:,5:6])
X = imp.transform(df.iloc[:,5:6])
scaler = preprocessing.scale(X)
print(scaler)数据降维
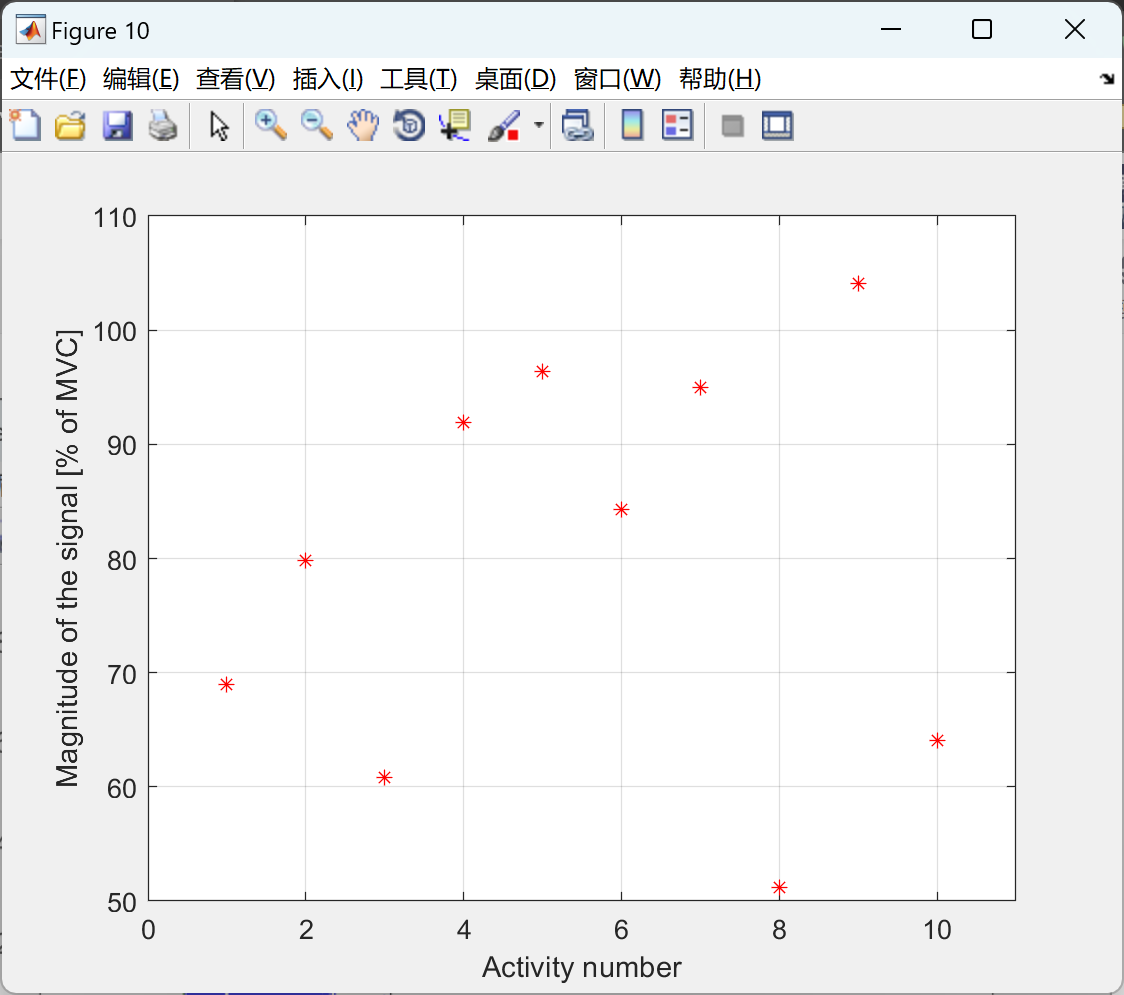
散点图分析(如何绘制散点图)
用来显示两组数据的相关性分布
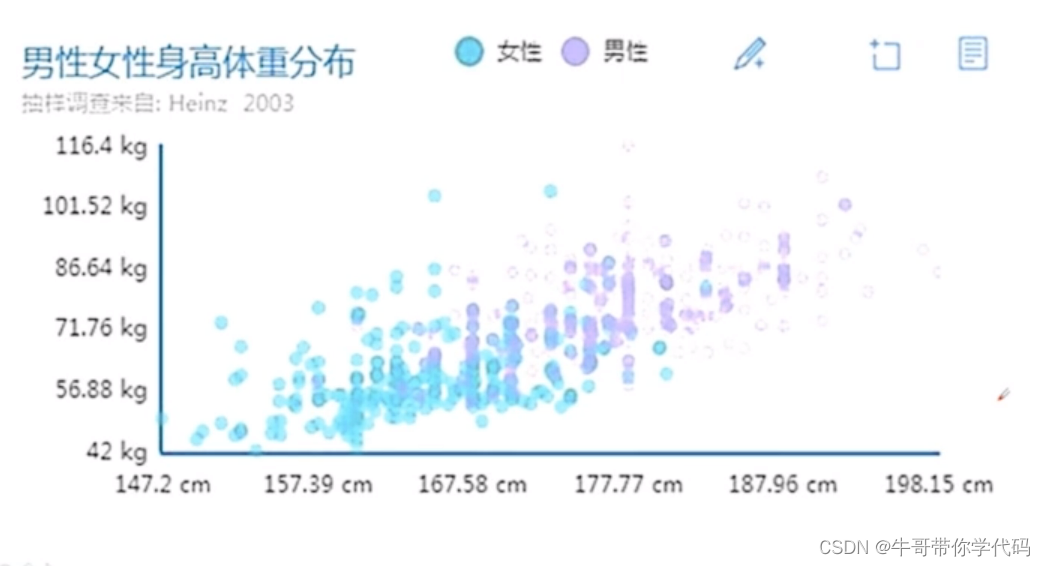
PCA(主成分分析)
直观理解(坐标轴的旋转)

在普通的XY轴坐标系,我们对每个点求方差,会发现方差比较大,也就意味着在X、Y轴上的信息量都比较大。因此不管舍弃哪一维都会损失数据的信息量。
通过PCA旋转,我们可以看到下面的图片,在长轴上数据的方差依然非常大,但是在短轴上方差非常小。方差小说明信息量就比较小。在这时,假如我们保留长轴数据,去掉短轴数据,对数据量的丢失也不会出现很明显的现象。
总的来说,PCA分析法就是通过坐标轴的旋转,将每个坐标轴信息量比较大的数据,经过旋转,使得在长轴上的信息量比较大。短轴上的信息量比较小。(实现了一种线性变换)
最终得到的结果形如
Z1=0.78*x1+0.01*x2+0.56*x3+0.067*x4
Z2=0.086*x1+0.76*x2+0.45*x3+0.97*x4
上面的主成分Z1、Z2分别由原来的四维数据(四种变量)降维得到。我们可以看到对于上面的二维数据我们可以看出来每种主成分中对应的变量的权值系数的不同。
权值系数的求解过程(了解即可):
对数据的相关矩阵求特征值特征向量,最后得到相应的权值
from sklearn.decomposition import PCA
import pandas as pd
data_url = "iris_train.csv"
df= pd.read_csv(data_url)
X = df.iloc[:,1:5]
y=df.iloc[:,5]
pca = PCA(n_components=4)
pca.fit(X)
print(pca.explained_variance_ratio_)绘制相关性矩阵图片(热力图)
使用热力图可以对相关性进行更清晰的描述和直观理解
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
train csv ='trainOX.csv'
train data = pdread csv(train_csv)
train data.drop(['ID','date','hour'],axis=1,inplace=True)
corrmat = train_data.corr()
f;ax = plt.subplots(figsize=(12,8))
sns.heatmap(corrmat, vmax=0.8, square=True)
plt.show()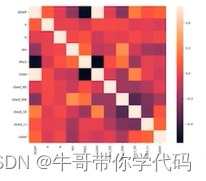
准确率评价
混淆矩阵
对于准确率的评价可以使用混淆矩阵的方法进行评估
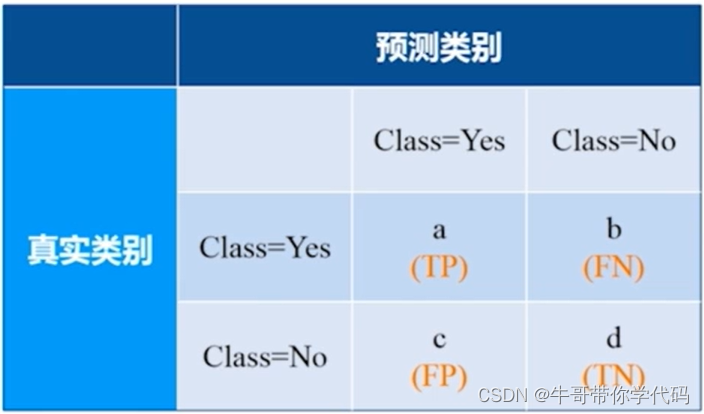
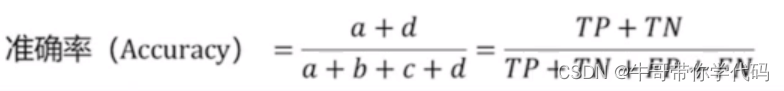
上述公式是准确率的计算公式
对应的左侧对应一列为样本中数据的真实类别。上边一行对应的是样本中数据的预测数据。
a对应的又称为真阳例(True Positive)、b对应的又称为假阴例(False Negative)、c对应的又称为假阳例(False Negative)、d对应的为真阴例(True Negative)。
对于各个类别的相关解释:
真阳例:指的是实际数据与预测数据结果相同的情况,数据本身为正类,我们把它预测为正类。(比如一部分用户是生病的,我们将其也预测为生病的,这样的用户数目即为真阳例)
假阴例:一个用户是生病的,但是通过模型预测的结果是没有生病的。
假阳例:本身是一个没有生病的客户,但是通过模型进行预测的结果为一个生病的客户,故为假阳例。
真阴例:客户没有生病,使用模型进行预测也没有生病。
显而易见上述混淆矩阵中,TP与TN是预测正确的(本身是正确的和本身不是正确的都预测准确了)。
对于数据检验部分,我们往往会将数据七三分为训练集和测试集两部分。
除此之外,我们往往也会使用K折交叉验证的方法对数据进行相关的验证。
K折交叉验证
在数据检验时,使用数据集中的倒数第k份数据进行检验,例如,第一次,使用倒数第1份数据进行检验;第二次检验,使用倒数第2份数据进行检验;第三次,使用倒数第3份数据进行检验....最多进行十折交叉验证。
知识点补充:
K-Means算法
优点
-
聚类时间快
-
当结果簇是密集的,而簇与簇之间区别明显时,效果较好
-
相对可扩展和有效,能对大数据集进行高效划分
缺点
-
用户必须事先指定聚类簇的个数
-
常常终止于局部最优
-
只适用于数值属性聚类(计算均值有意义)
-
对噪声和异常数据也很敏感
-
不同的初始值,结果可能不同
-
不适合发现非凸面形状的簇