多源
- 超级源点和汇点
- 最短距离[超级汇点]
- 昂贵的聘礼
- 多源BFS
- 矩阵距离
超级源点和汇点
超级源点跟超级汇点是模拟出来的虚拟点,多用于图中:
<1>同时有多个汇点和一个源点,建立超级汇点
1、2、3、6分别到达4或者5或者7的最短路径,设立0这个超级汇点。
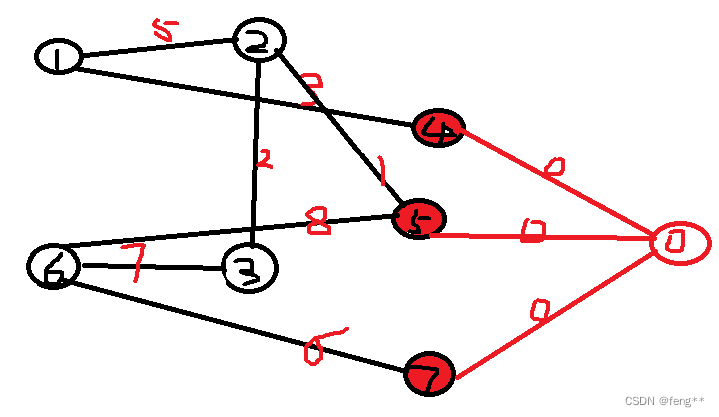
<2>同时有多个源点和一个汇点,建立超级源点
<3>同时有多个源点和多个汇点,建立超级源点和超级汇点
最短距离[超级汇点]
题目连接:https://www.acwing.com/problem/content/1490/
思路分析:这个题的关键就在于模拟出来一个超级汇点,对于每个村庄来说,目的地都是一个商店,具体是哪一个商店是不要求的,只需要找到最近的一个商店,也就是找到到这些商店集合的最短路径,虚拟出来一个超级汇点,到这些商店的路径都为0,这样每个村庄到达集合的最短路径其实就是到达这个超级汇点的最短路径了,也就相当于是这个超级汇点到每个点的最短路径,进行一次dijstra就行,也就简化成了求点到点的最短路径。
AC代码:
#include<iostream>
#include<queue>
#include<vector>
using namespace std;
const int N=100005;
const int INF=0x3f3f3f3f;
typedef pair<int,int>PII;
vector<PII>adj[N];
int dist[N];
bool visited[N];
int n,m,k,q,x;
priority_queue<PII,vector<PII>,greater<PII>>que;void dijistra(int s)
{for(int i=0;i<=n;i++) dist[i]=INF; dist[s]=0; que.push({0,s});while(!que.empty()){int min=que.top().second;que.pop();if(visited[min]) continue;visited[min]=true;for(int i=0;i<adj[min].size();i++){if(!visited[adj[min][i].first]&&dist[min]+adj[min][i].second<dist[adj[min][i].first]){dist[adj[min][i].first]=dist[min]+adj[min][i].second;que.push({dist[adj[min][i].first],adj[min][i].first});}}}
}
int main()
{cin>>n>>m;while(m--){int u,v,c; cin>>u>>v>>c; adj[u].push_back({v,c}); adj[v].push_back({u,c});}cin>>k;while(k--){cin>>x; adj[0].push_back({x,0}); adj[x].push_back({0,0});}dijistra(0); cin>>q; while(q--){cin>>x; cout<<dist[x]<<endl;}return 0;
}
昂贵的聘礼
刷题链接:https://www.acwing.com/problem/content/905/
思路分析:到底怎么建立图是很关键的,必要的时候要加一些超级源点和超级汇点
还是注意要建立一个超级源点,表示最后终止继续交换下去的那个人的花费是他的物品的价格;
最后要保证求出来的最短路包含的结点的等级相互之间都不超过m,只能是枚举这个等级区间了,不能说每次更新邻接结点的时候判断该结点距离当前纳入最短路径集合的结点的距离,如果超过了m就不更新,这样只能保证相邻的两个结点的等级是不超过m的,但是最后最短路径包含的全部结点相互间不一定都不超过m,规则是只要跟一个很高的人交换了,后面涉及的所有等级很低的人都不能再进行交换
AC代码:
#include<iostream>
#include<queue>
#include<vector>
#include<algorithm>
using namespace std;
const int N=105;
const int INF=0x3f3f3f3f;
typedef pair<int,int>PII; //first表示未结点编号,second表示到达该结点的优惠
vector<PII>adj[N];
int dist[N];
bool visited[N];
int m,n,p,l,x,t,v;
int Rank[N]; //存储每个结点的等级
priority_queue<PII,vector<PII>,greater<PII>>que;int dijistra(int down,int up) //传入区间等级最大和最小值
{for(int i=0;i<=n;i++){dist[i]=INF; visited[i]=false;}dist[0]=0;que.push({0,0});while(!que.empty()){int min=que.top().second;que.pop();if(visited[min]) continue;visited[min]=true;for(int i=0;i<adj[min].size();i++){//超级源点跟谁都能到达 if(Rank[adj[min][i].first]>up||Rank[adj[min][i].first]<down) continue; //等级相差太大,无法到达 if(!visited[adj[min][i].first]&&dist[min]+adj[min][i].second<dist[adj[min][i].first]){dist[adj[min][i].first]=dist[min]+adj[min][i].second;que.push({dist[adj[min][i].first],adj[min][i].first});}}}return dist[1];
}
int main()
{cin>>m>>n;for(int i=1;i<=n;i++){cin>>p>>l>>x;adj[0].push_back({i,p}); //建立超级源点到该点的边权Rank[i]=l;while(x--) //替代品们 {cin>>t>>v;adj[t].push_back({i,v}); //建立替代品到该点的边权} }int ans=INF;for(int i=Rank[1]-m;i<=Rank[1];i++){ans=min(ans,dijistra(i,i+m)); //超级源点到每个点的最短路径 }cout<<ans<<endl; return 0;
}
多源BFS
单源BFS:起始阶段只需要将某一个元素加入队列
二叉树层序遍历
多源BFS:开始阶段加入多个元素入队列,可以将其理解为存在一个超级源点,然后进行宽搜扩展,第一阶段会把距离为0的点扩展进队列进行求解最短距离,第二阶段会把距离为1的点扩展进队列进行求解最短距离,第三阶段会把距离为2的点扩展进队列进行求解最短距离,…最后成功将所有点距离目标点的最短距离求出来了。
矩阵距离
题目链接:https://www.acwing.com/problem/content/description/175/
思路分析:曼哈顿距离实际就是从1位置处向外扩展,每次扩展距离加1
AC代码:
#include<iostream>
#include<bits/stdc++.h>
using namespace std;
int n,m;
typedef pair<int,int>PII;
queue<PII>tou;
const int INF=0x3f3f3f3f;
const int N=1005;
int grid[N][N];
int off[4][2]={{0,-1},{0,1},{-1,0},{1,0}};
int main()
{cin>>n>>m;for(int i=0;i<n;i++){for(int j=0;j<m;j++){char t;cin>>t;if(t=='1') {grid[i][j]=0;tou.push({i,j});}else grid[i][j]=-1;}}while(!tou.empty()){int x=tou.front().first;int y=tou.front().second;tou.pop();for(int i=0;i<4;i++){int xi=x+off[i][0],yi=y+off[i][1];if(xi>=0 && yi>=0 &&xi<n && yi<m && grid[xi][yi]<0){tou.push({xi,yi});grid[xi][yi]=grid[x][y]+1;}}}for(int i=0;i<n;i++){for(int j=0;j<m;j++){cout<<grid[i][j]<<" ";}cout<<endl;}return 0;
}