红黑树模拟实现并封装为map和set
- 前言
- 正式开始
- 红黑树概念
- 红黑树基本要求
- 大致框架
- 树节点
- 树
- 调整红黑树使其平衡
- 第一种:cur红,p红,g黑,u存在且为红
- 第二种:cur红,p红,g黑,u不存在或为黑
- 左左,右右:单旋 + 变色
- 左右,右左:双旋 + 变色
前言
本篇主要讲解红黑树的模拟实现,实现之后再封装成map和set。
红黑树中所用到的旋转功能均源自我的上一篇博客,本篇中不会再详谈旋转,若对于旋转不了解的同学可以先看看上一篇博客:【C++】AVL树模拟实现插入功能
正式开始
前一篇的AVL树,是严格平衡的一棵二叉搜索树,也就是每个节点的做右子树高度差不超过1。
红黑树,在二叉搜索树的基础上,多了一个条件:最长路径不超过最短路径的2倍。没有AVL树那么严格,但是也是近似平衡的。
同AVL树相比,插入同样的数据,AVL树旋转更多,红黑树旋转更少,红黑树的优势就在于此,这一点比AVL树优很多,毕竟每次旋转的时候还是要动不少指针的。
但同时红黑树也有一丁点的劣势,查找效率比AVL树低一丢丢,因为极端情况下,也就是最长路径就是最短路径的2倍时,当我们正好要查找最长路径的叶子节点时,速度比AVL树慢了一半。但是虽说是一半,那也只是 l o g 2 N log_2N log2N的一半,如果存储10亿个数,查找最边上的节点,也就查找30次就能找到,因为对于AVL树来说几乎是完全二分的,那么红黑树的最坏情况就是60次喽,但是这样二者相差可以说是忽略不计的。
所以考虑整体情况的话,还是红黑树更胜一筹。不然STL中的map和set底层用的就不是红黑树了。
红黑树概念
红黑树,是一种二叉搜索树,但在每个结点上增加一个存储位表示结点的颜色,可以是Red或Black。 通过对任何一条从根到叶子的路径上各个结点着色方式的限制,红黑树确保没有一条路径会比其他路径长出俩倍,因而是接近平衡的。
先来一棵树看看:
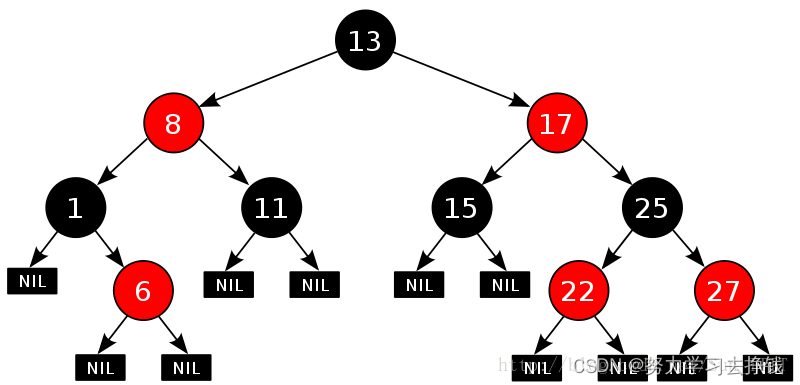
看起来花里胡哨的,不要怕,纸老虎。
红黑树基本要求
红黑树实现的时候不是按照AVL树那样依靠平衡因子来实现的。而是通过控制节点是红色还是黑色来实现的,不然也就不叫红黑树了。
但是对于节点是红色还是黑色是有要求的:
- 每个节点非黑即红
- 根节点是黑色的
- 红色节点的两个子节点为黑色的,即树中没有连续的红色结点
- 对于每个结点,从该结点到其所有后代叶结点的简单路径上,均包含相同数目的黑色结点。即每条路径上黑色结点数相等。
- 每个叶子结点都是黑色的(此处的叶子结点指的是空结点)。
第五点其实没什么用,是指空节点是黑色节点,当树是空树的时候正好可以和第二条对应。树是空树,根节点就是空的,空节点是黑色节点,那么根节点也就是黑色结点了。
我再把上面那张图拿出来,各位对着前四点看看:
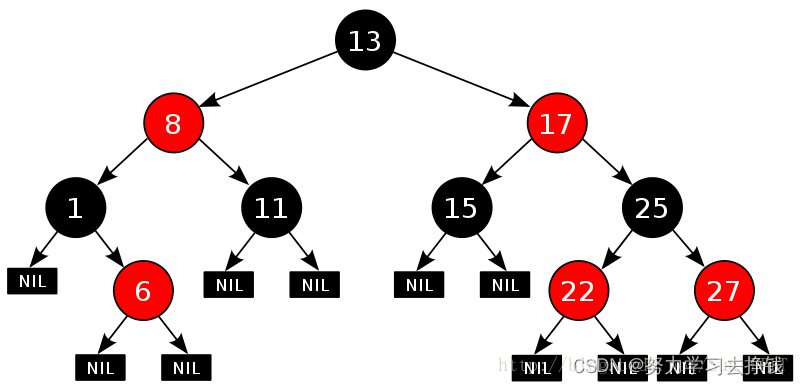
每个结点满足上述条件后就能够保证最长路径不超过最短路径的二倍了。各位想想为什么。
上述条件中可没有说不能有连续的黑色节点,所以最短路径就可以是连续黑色结点所组成的路径,最长路径就是一黑一红一黑一红…组成的路径。那么当到达极限时,最长路径就正好是最短路径的二倍。
再问个问题:
上图中,一共有几条路径?
答案是:11条。
有的同学可能懵了,不要懵。
上面数路径是要数到空节点的,上面一共有11个空节点,所以也就是11条路径。
这里也是第五点的一个好处,方便我们数路径,可以看到图中空节点写的是NIL,红黑树这里把空节点叫做NIL节点。
废话不多说了,我们先把树大致框架搞出来。
大致框架
树节点
红黑树树节点中包含的东西如下:

构造函数为:

颜色暂时不给,等会插入的时候会再说。
树
再来写树。
初始就一根:

然后把二叉搜索树的基本的插入功能写出来:

上面我把调整树结构的留下,这里细讲。
调整红黑树使其平衡
若插入新节点后的树结构不符合了前面说的那四条规则,此时就要调整。
但是插入节点要确定一下其颜色,如何确定呢?
看第三条和第四条规定。不能有连续的红色节点,所有路径黑色节点数量相同。
所以如果我们插入红色节点,影响的就只是当前插入节点所处的路径,因为红色节点不相连即可。如果我们插入黑色结点,影响的就是整棵树了,因为当前路径加一个黑的,其他路径就都要加一个黑的。显然,我们要选就选红色的插入,千万不敢选黑色的插,一选黑色就要调整棵树,选了红色只调当前路径就够了。
那么调整之前,我得先声明几个节点的名字
- cur节点,就是新插入的节点,等会在调整的过程中我以cur表示。
- . 父(father)节点 / 双亲(parent)节点, 等会在调整的过程中我以字母p表示。
- 叔叔(uncle)节点,就是父节点的兄弟,等会在调整的过程中我以字母u表示。
- 爷爷(grandfather)节点,就是父节点的父节点,等会在调整的过程中我以字母g表示。
先来个图看看:
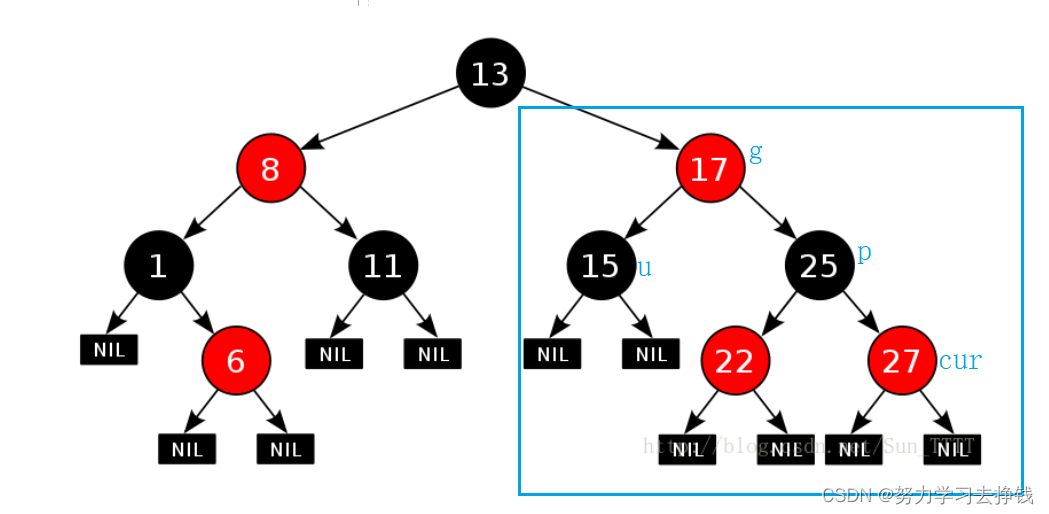
那么调整可分为两大种情况。
第一种:cur红,p红,g黑,u存在且为红
第二种:cur红,p红,g黑,u不存在或为黑
说一下为啥是上面两种。
首先我们插入的一定是红色节点。
- 树为空的时候,不需要调整,直接让根搞成黑色节点。
- 插入节点为红色,p为黑色,此时不需要调整,直接插入即可。因为前面也说了,极限长度是黑红黑红这样规律走下去的,当插入的是红色的时候,不会出现到达最长路径的情况。所以不需要调整。
- 插入节点为红色,p为红色,违反第三条规定,此时就需要调整。而且当p为红色的时候,g一定为黑色,因为原树要保证是红黑树,所以当p是红色的时候,不能有连续的红色节点,所以g就一定是黑色的。
然后将第三点的调整分为两大种,至于为什么,等会将调整的时候就知道了,这是前人总结出来的规律。
那么就开始将调整。
如果你对于AVL树插入时的旋转非常熟悉了,那么这里红黑树插入的调整自然也不在话下。
正式开始调整:
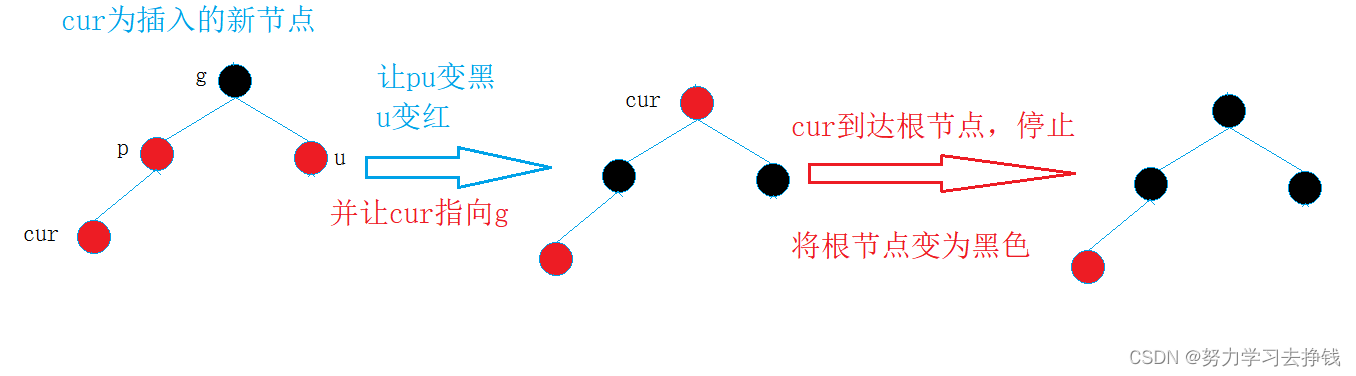
第一种:cur红,p红,g黑,u存在且为红
调整方式为:pu变黑g变红,cur指向g继续向上调整,遇到树根为止,将树根改为黑。
即只有变色。
先来两个例子:
调整一次:
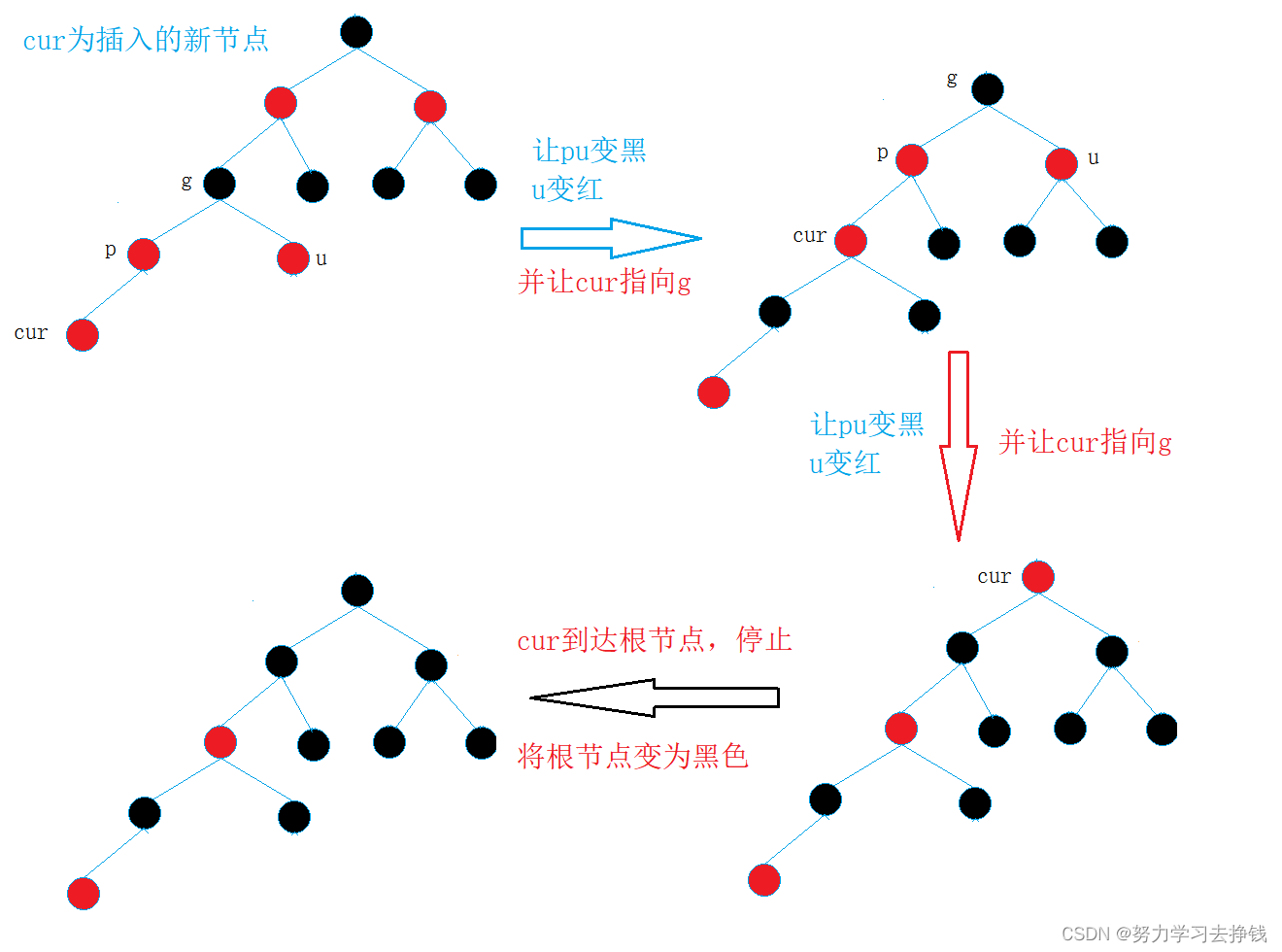
调整两次:
不用往下画了,再往下就是调整三、四、五……等等次数了。是有规律的,上面两个都是具象图,下来我把抽象图给大家,各位参考参考:
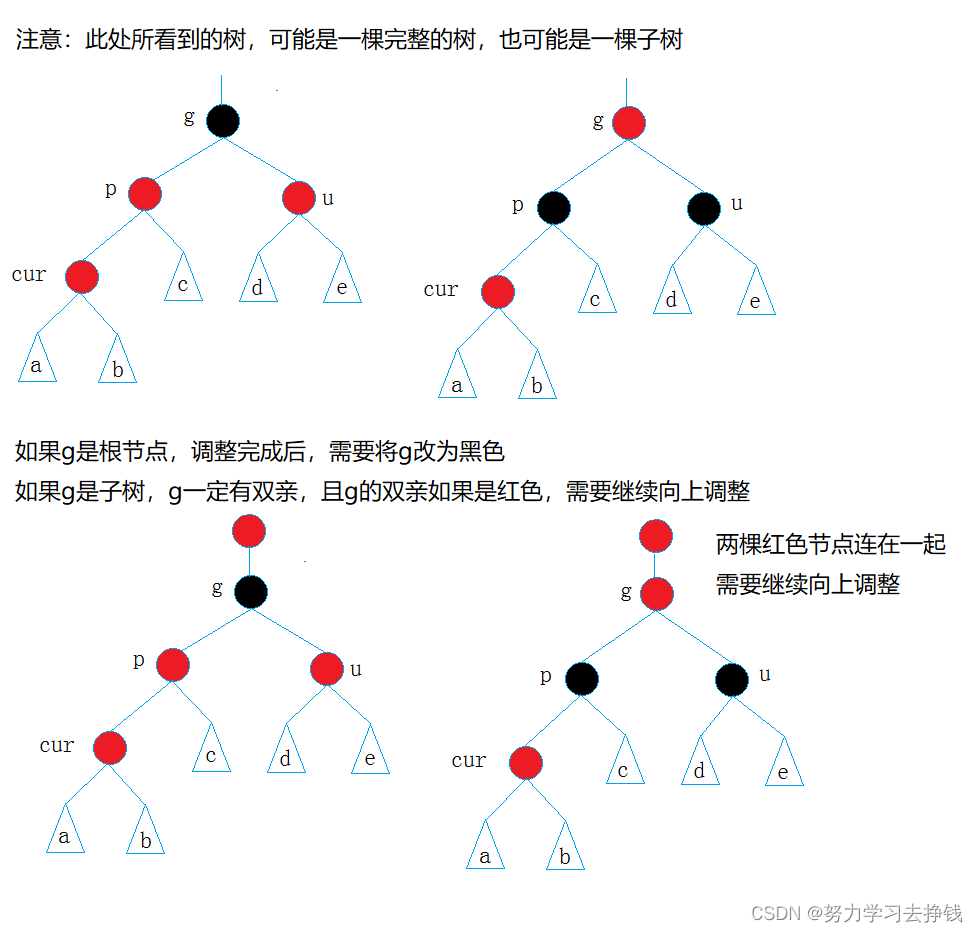
附上我手画的图:
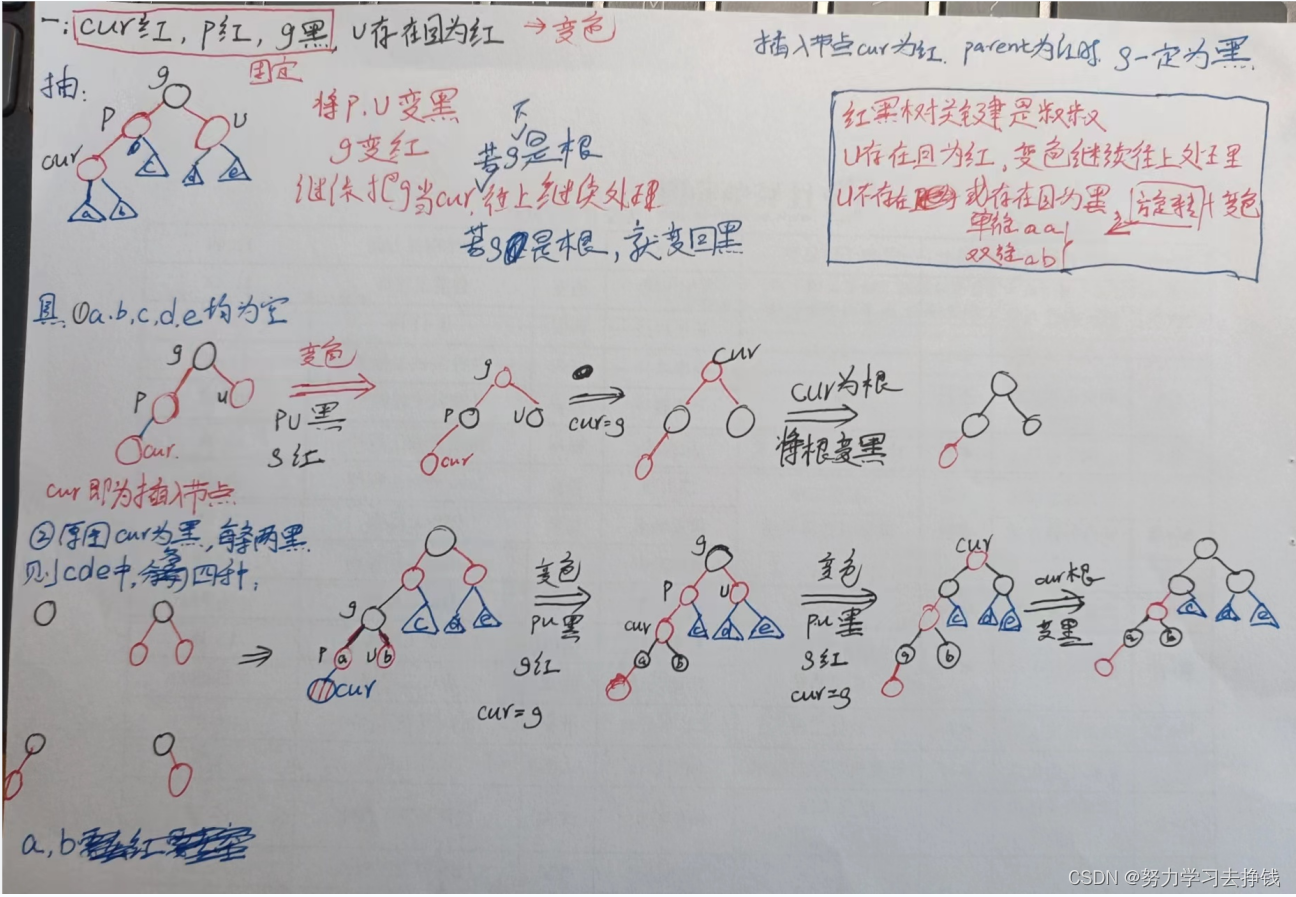
比较潦草,主要是方便我看一下。
这里不管cur在p左边还是右边,调整方式都是一样的,记住最开始写的调整方式就行:
调整方式为:pu变黑g变红,cur指向g继续向上调整,遇到树根为止,将树根改为黑。
即只有变色。
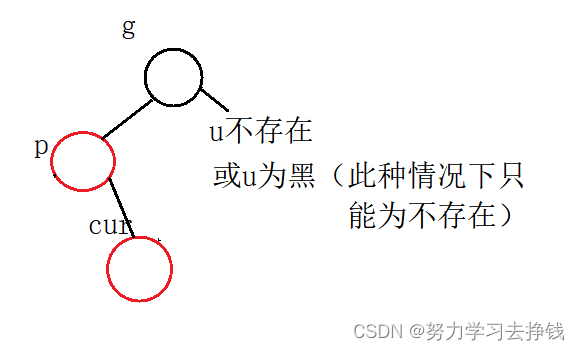
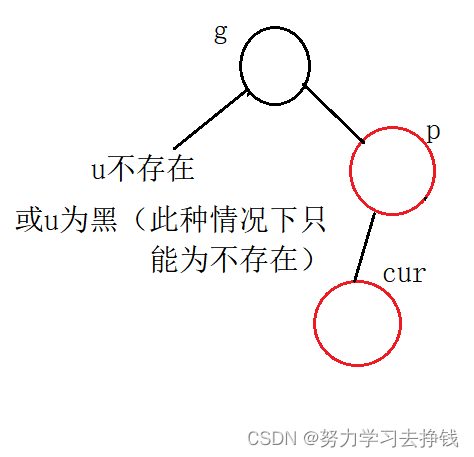
第二种:cur红,p红,g黑,u不存在或为黑
第二大种就要用到旋转了,但还要再分为两小种。
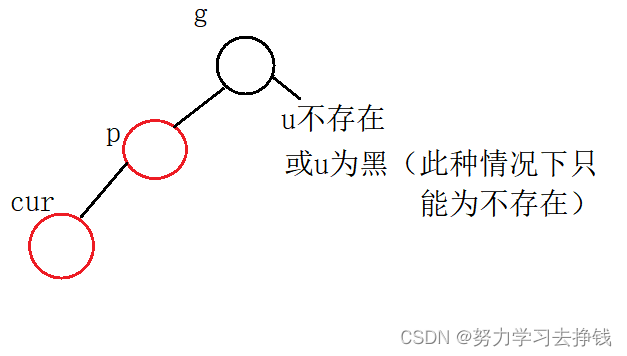
第一小种:p在g左且cur在p左,或者p在g右且cur在p右。此种情况下为单旋。
对应的图为:
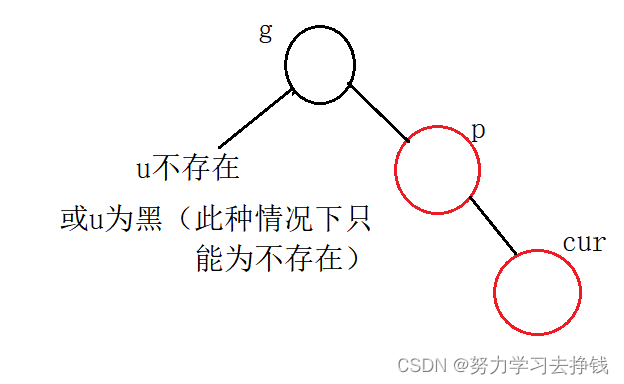
第二小种:p在g左且cur在p右,或者p在g右且cur在p左。此种情况下为双旋。
对应图为:
然后再细谈:
左左,右右:单旋 + 变色
单旋 + 变色。
和AVL树一样,左左就右单旋,右右就左单旋。
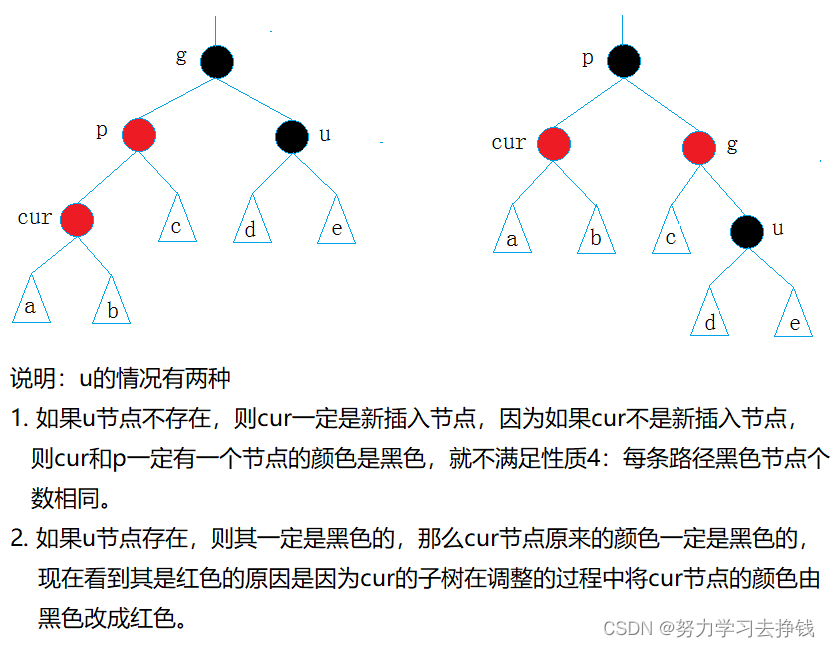
我就只画左左的,还是先给两个实例的图,再给抽象图。
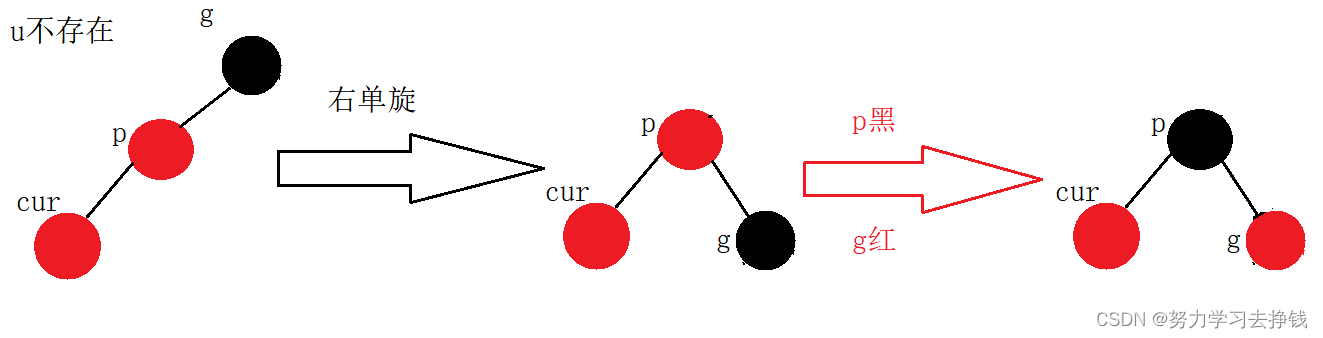
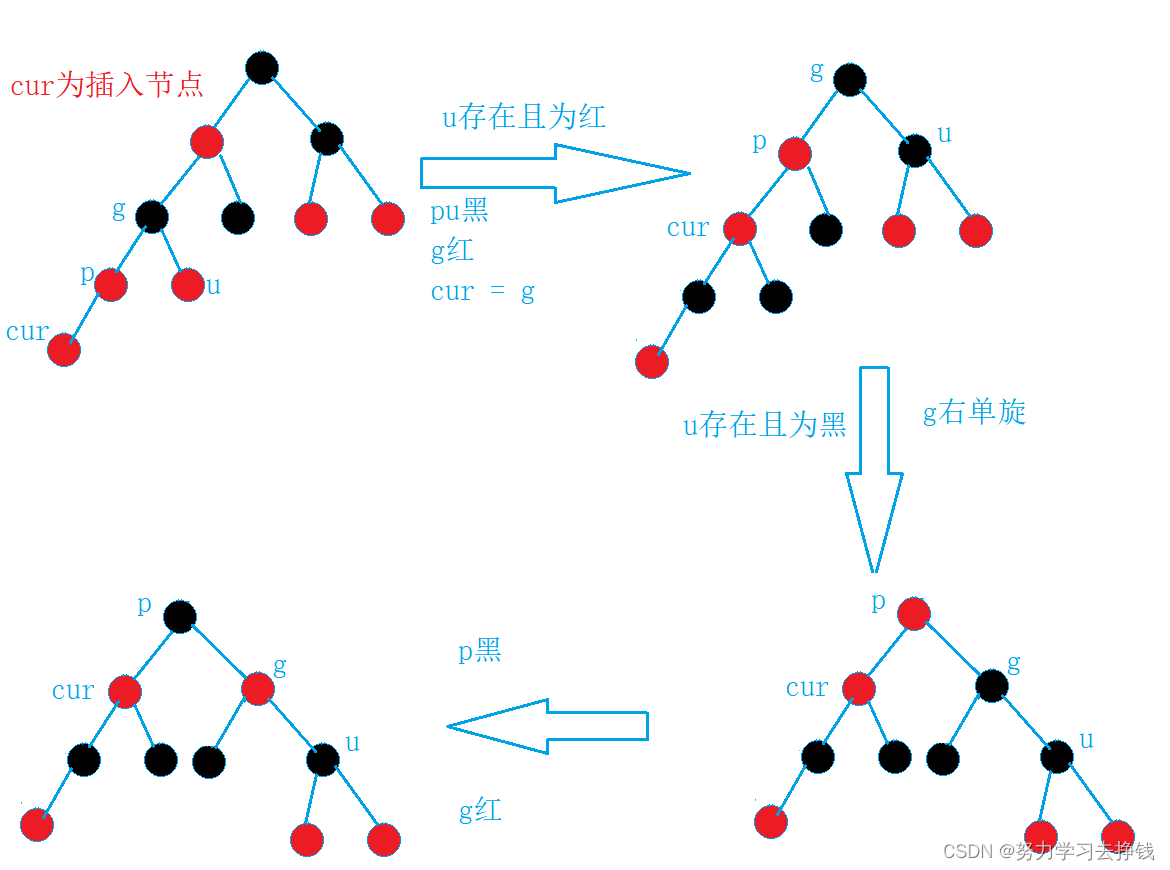
抽象图:
左右,右左:双旋 + 变色
单旋 + 变色。
和AVL树一样,左右就左右双旋,右左就右左双旋。
实例:
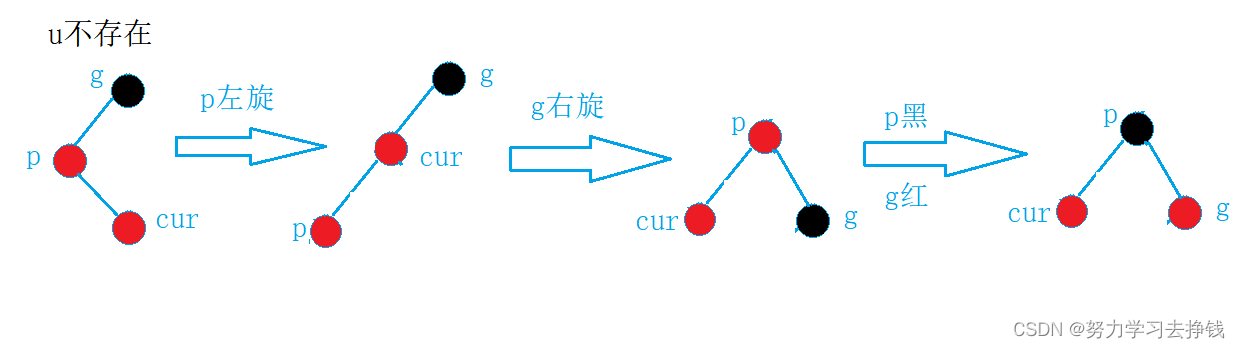
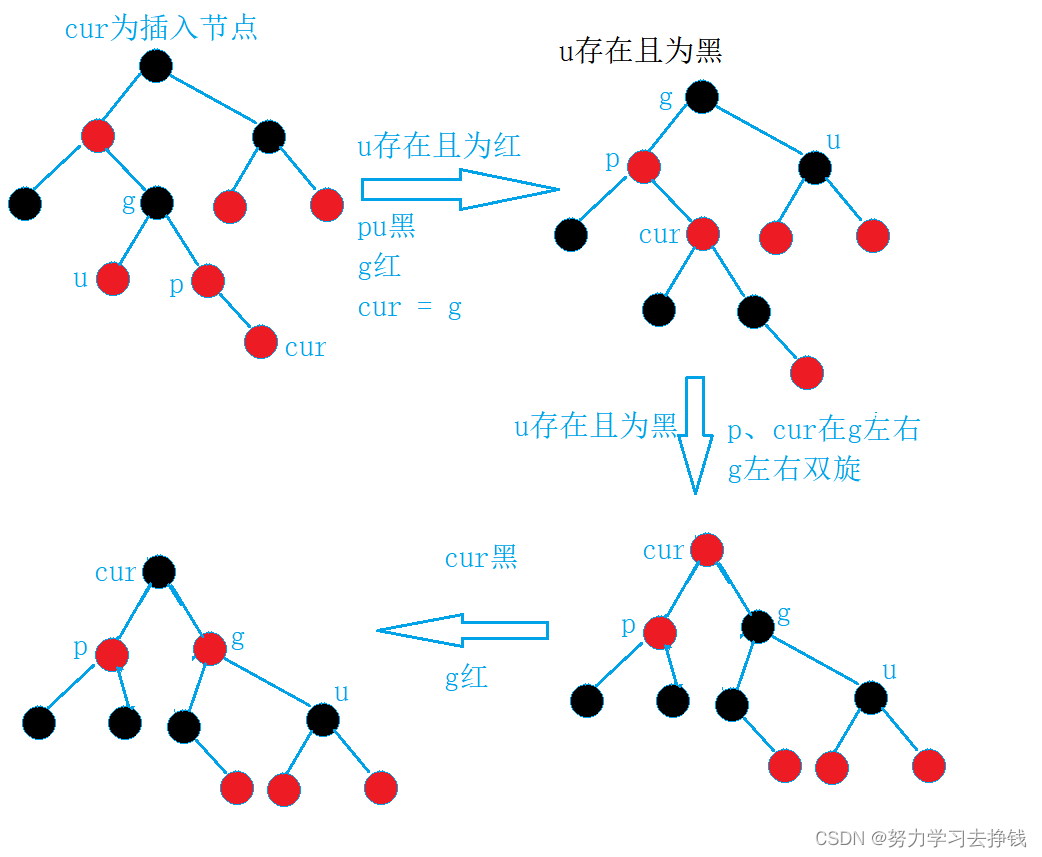
抽象图:
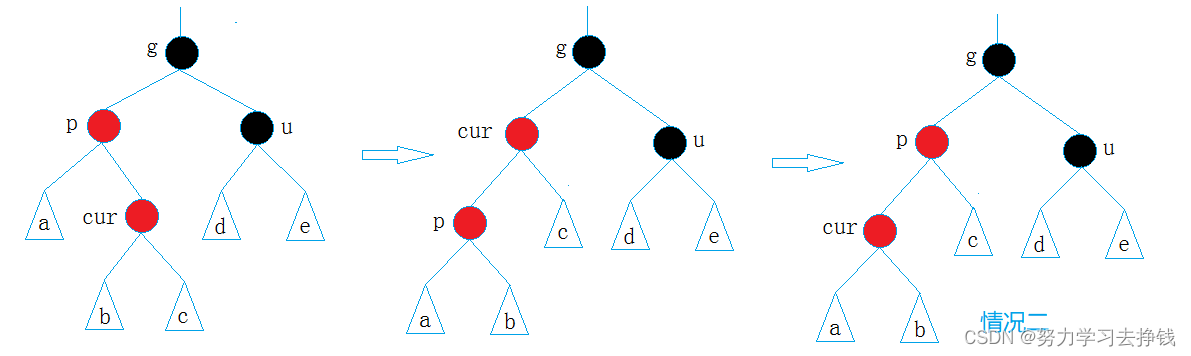
手画图:
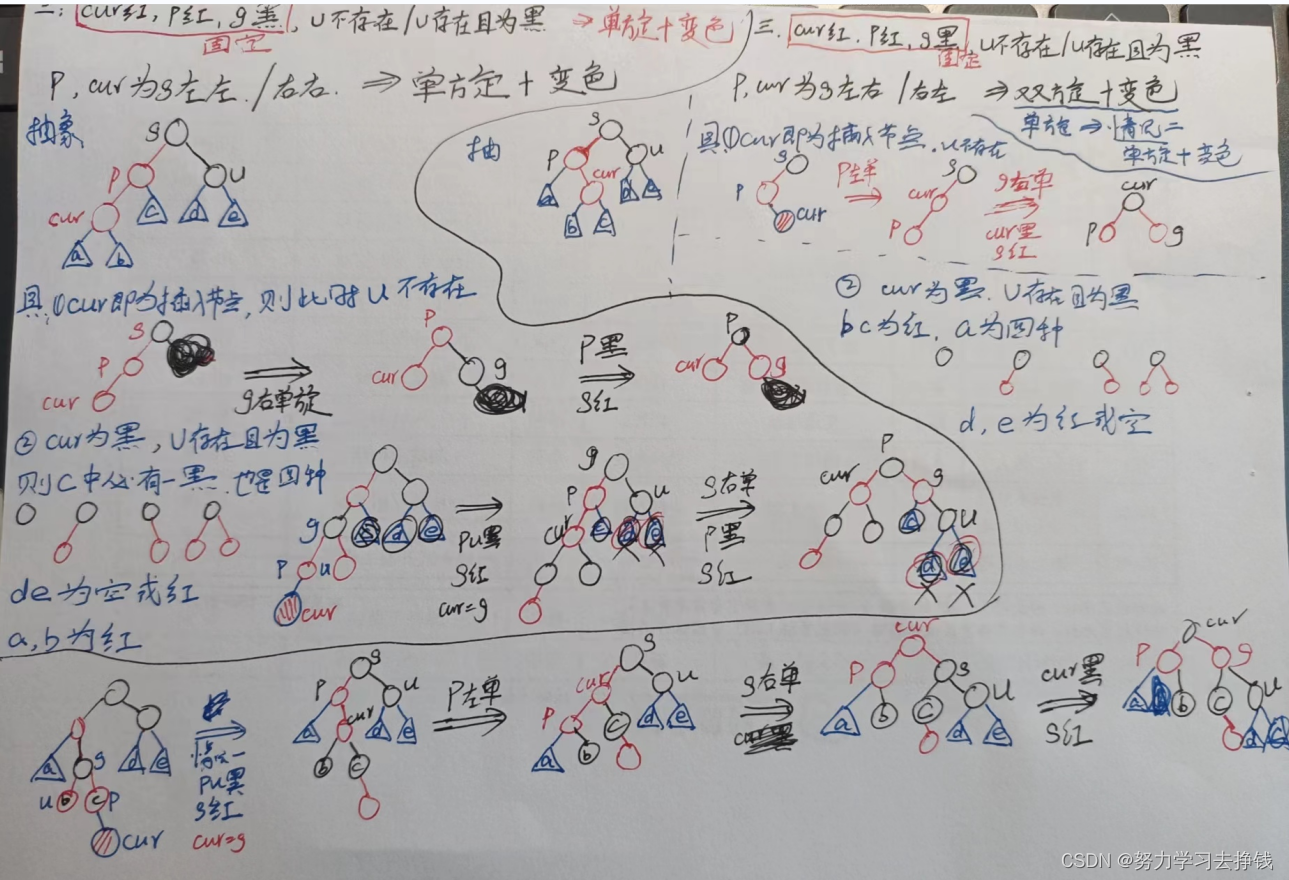
总结一下:
红黑树调节平衡关键是看叔叔。
u存在且为红,变色继续往上处理。
u不存在 或者 存在且为黑,旋转+变色。其中旋转又分单旋和双旋,若p、cur在单侧,就单旋,若p、cur一左一右或一右一左就双旋。
上面的三种情况搞完就可以写代码了。
调节平衡的代码如下:

其中我光用了单旋,没有用双旋,因为双旋就是两个单旋。
单旋代码:

可以写一个中序遍历来简单打印一下结果:


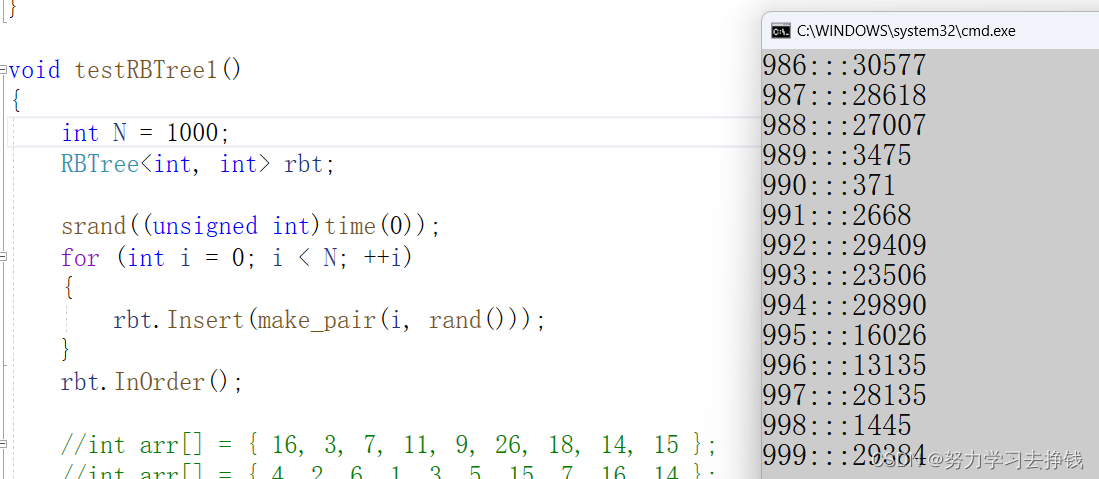
但是简单的中序遍历可不够,来写一个专门用来检查是否平衡的函数。

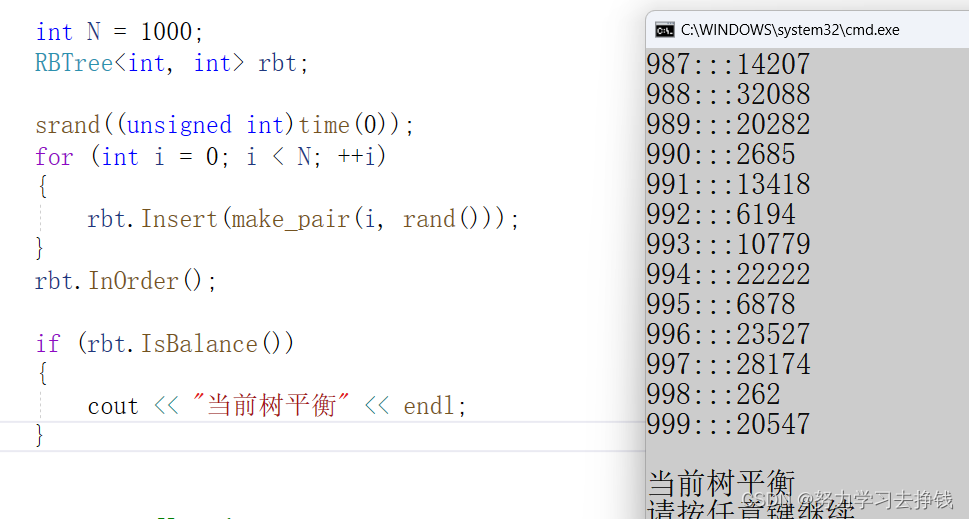
到此结束。。。