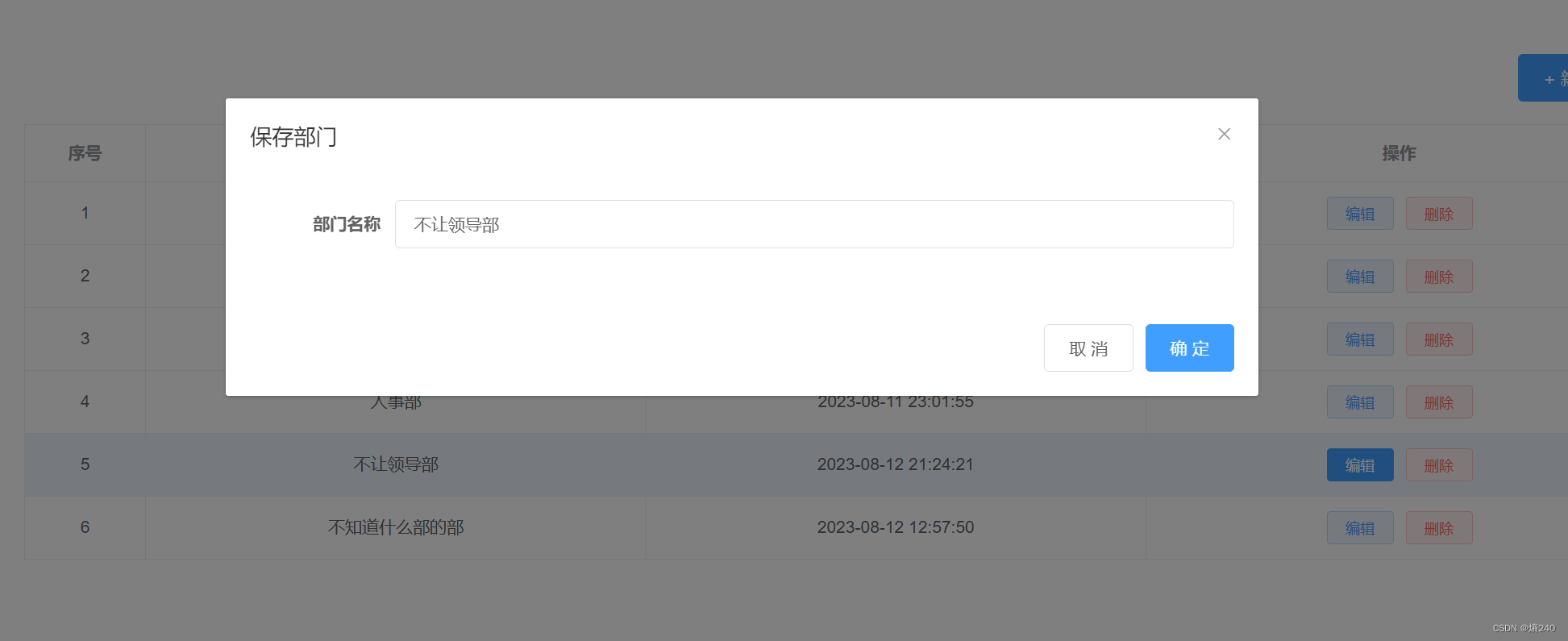
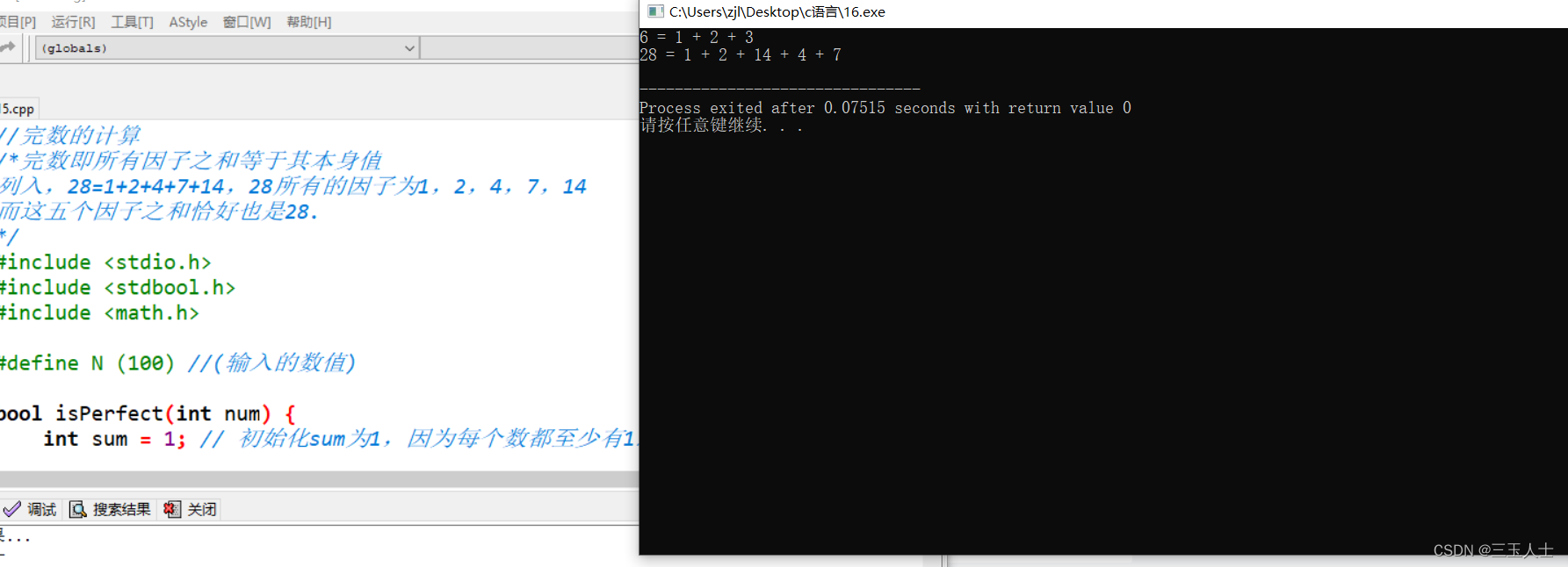
完数即所有因子之和等于其本身值
列入，28=1+2+4+7+14，28所有的因子为1，2，4，7，14
而这五个因子之和恰好也是28. 

//完数的计算
/*完数即所有因子之和等于其本身值
列入，28=1+2+4+7+14，28所有的因子为1，2，4，7，14
而这五个因子之和恰好也是28. 
*/ 
#include <stdio.h>
#include <stdbool.h>
#include <math.h>#define N (100) //(输入的数值)bool isPerfect(int num) {int sum = 1; // 初始化sum为1，因为每个数都至少有1这个因子for (int i = 2; i <= sqrt(num); i++) {if (num % i == 0) {sum += i;if (i != num / i) {sum += num / i;}}}return sum == num;
}int main() {for (int i = 2; i <= N; i++) {if (isPerfect(i)) {printf("%d = 1", i);for (int j = 2; j <= sqrt(i); j++) {if (i % j == 0) {printf(" + %d", j);if (j != i / j) {printf(" + %d", i / j);}}}printf("\n");}}return 0;
}
/*
引入stdbool.h头文件，使用bool类型来表示是否为完全数。
定义了一个辅助函数isPerfect，该函数接受一个整数参数，判断该数是否为完全数。
在isPerfect函数中，只需要遍历2到sqrt(num)之间的数即可，将因子及其对应的补因子同时相加，以减少计算次数。
在isPerfect函数中，使用bool类型来返回判断结果。
在主函数中，调用isPerfect函数来判断每个数是否为完全数，并输出结果。
修改了循环变量的命名以提高代码可读性。
*/