这一章还是很重要的,可以看到为什么dt1^dt2和dt1dt2是一样的。

可以看到,核心还是黎曼和,我们把两种微分的黎曼和都列出来,并且证明两个相等,即可。
这里要注意,微分形式的积分,在黎曼和的情况下是带作用的变量的。这里还看不出来,因为它没有写出微分形式的黎曼和。我们后面看就清楚了。
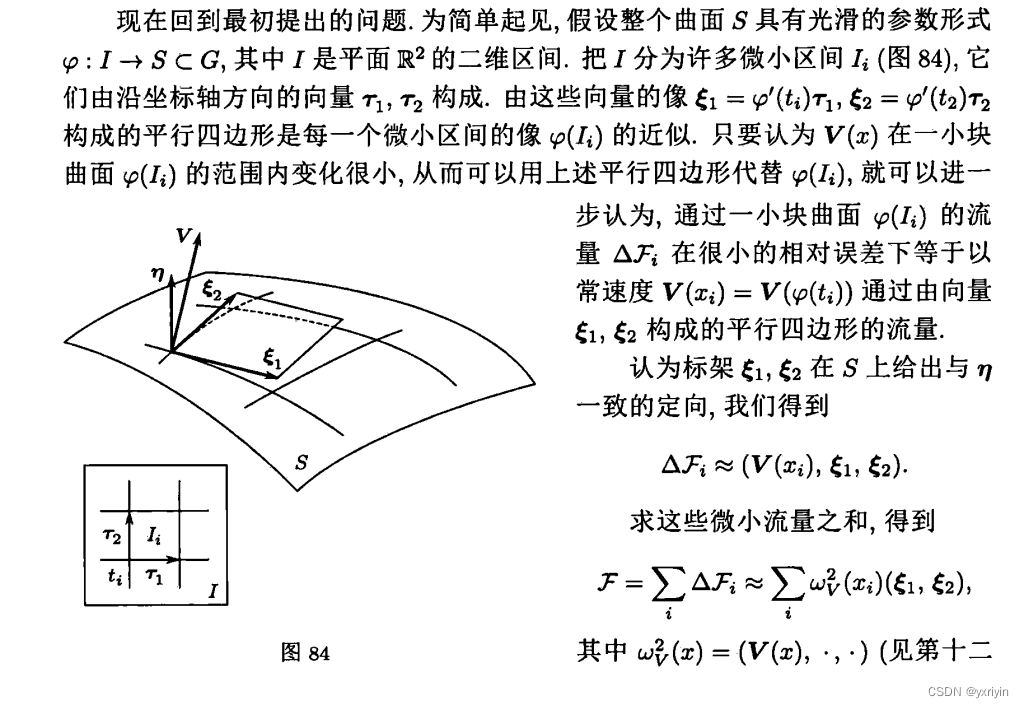
这是流形式,可以看到2形式的黎曼和。是需要作用在两个向量上的。
这里很重要,可以卡拿到,相比起之前我们普通积分的黎曼和肯定会写出dt1dt2,微分形式的黎曼和的积分是省略后面的dt1^dt2的,或者是这个部分被合并到了2形式里面。当然你也可以展开它,就会变成公式(4)

利用变量代换或者拉回,我们可以得到两个不同的黎曼和是相等的。而其中一个黎曼和可以进一步化简成为我们熟悉的面积,而这个就转化成了我们熟悉的普通积分。也就证明了外微分形式和普通微分的等价性。
后面的推导就是水到渠成了。

接下来我们需要把上面的推导扩展到k维曲面上去。

这一段很长,其实就是假定phi是恒等映射的时候得到的结论。这里要注意,前面虽然证明了外积和普通微分乘积是等价的,但微分形式的积分通过变量代换后,还是会有一个额外的雅克比行列式。这里是认为这个变量代换是恒等映射,那么雅克比行列式就相当于1了。
后面这个定义的合理性证明书上写的相对比较模糊,还是看老师的课程更好。这里我就不展开说明了,感觉有点费脑子,绕口。核心就是你需要证明在两个不同的标架下,两个的积分是相等的。我们先写出其中一个标架的积分,然后把另一个标架的积分通过变量代换公式转过来。然后证明转换后的两者是相等的即可。

接下来是体形式的相关内容:

前面格拉姆矩阵求面积的公式,现在用在这里看看。

这里引出了面积正负的问题,为了解决这个问题,引出了体形式:

这里我看了很久,始终没理解这个公式怎么来的,后来仔细看了原来的内容,发现竟然如此简单:


之前看这一段,理解不够深入,只是单纯认为k反对称形式可以看成f(t)dx1^dx2....这样,但其实这个公式是非常重要的:
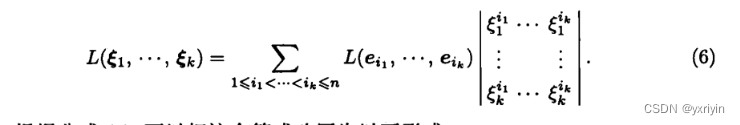
如果我们把e1,e2看成一组标准正交基,而kexi1,kexi2.。。看成另一组标准正交基,那么他们的关系就是相差一个行列式,而这个行列式正式从kexi空间转到e空间的矩阵的转置。
而体形式中:

因为变换矩阵是正交的,转置其实就是逆矩阵,所以就是e转到kexi空间的矩阵。所以公式是显然成立的。