今日份题目：

给定两个字符串s1 和 s2，返回 使两个字符串相等所需删除字符的 ASCII 值的最小和 。

示例1

输入: s1 = "sea", s2 = "eat"
输出: 231
解释: 在 "sea" 中删除 "s" 并将 "s" 的值(115)加入总和。
在 "eat" 中删除 "t" 并将 116 加入总和。
结束时，两个字符串相等，115 + 116 = 231 就是符合条件的最小和。

示例2

输入: s1 = "delete", s2 = "leet"
输出: 403
解释: 在 "delete" 中删除 "dee" 字符串变成 "let"，
将 100[d]+101[e]+101[e] 加入总和。在 "leet" 中删除 "e" 将 101[e] 加入总和。
结束时，两个字符串都等于 "let"，结果即为 100+101+101+101 = 403 。
如果改为将两个字符串转换为 "lee" 或 "eet"，我们会得到 433 或 417 的结果，比答案更大。

提示

• 0 <= s1.length, s2.length <= 1000

• s1 和 s2 由小写英文字母组成

题目思路

动态规划，依旧是使用二维dp数组记录子问题到当前问题的决定。

状态转移方程：

当当前两个位置的字符相同时，就更新为前边两个位置的dp值即可；当前两个位置的字符不同时，就需要找到前边两个位置中ASCII码小的那个加入到前一个子问题中：

if(c1==c2) 
{dp[i][j]=dp[i-1][j-1];
} 
else 
{dp[i][j]=min(dp[i-1][j]+s1[i-1],dp[i][j-1]+s2[j-1]);
}

代码

class Solution 
{
public:int minimumDeleteSum(string s1, string s2) {//获取两个字符串的长度int n=s1.size();int m=s2.size();//获取字符串ASCII码int a;for(int i=0;i<n;i++) a+=s1[i];int b;for(int i=0;i<m;i++) b+=s2[i];if(n==0) return b;else if(m==0) return a;int dp[2000][2000]={0};//更新边界值for(int i=1;i<=n;i++) {dp[i][0]=dp[i-1][0]+s1[i-1];}for(int j=1;j<=m;j++) {dp[0][j]=dp[0][j-1]+s2[j-1];}//更新所有dp值for(int i=1;i<=n;i++) {char c1=s1[i-1];for(int j=1;j<=m;j++) {char c2=s2[j-1];if(c1==c2) {dp[i][j]=dp[i-1][j-1];} else {dp[i][j]=min(dp[i-1][j]+s1[i-1],dp[i][j-1]+s2[j-1]);}}}return dp[n][m];}
};

提交结果

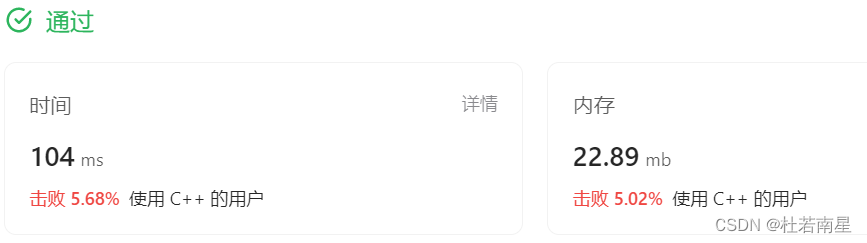
 欢迎大家在评论区讨论，如有不懂的代码部分，欢迎在评论区留言！