- 博主简介:努力学习的22级计算机科学与技术本科生一枚🌸
- 博主主页: @是瑶瑶子啦
- 每日一言🌼: 所谓自由,不是随心所欲,而是自我主宰。——康德
目录
- 一、前言
- 二、刷题
- 1、最大二叉树
- 2、从前序与中序遍历序列构造二叉树
- 3、从中序与后序遍历序列构造二叉树
- 4、 根据前序和后序遍历构造二叉树
一、前言
🍊 二叉树的构造问题一般都是使用「分解问题」的思路:构造整棵树 = 根节点 + 构造左子树 + 构造右子树
( 关键在于明确递归函数的定义,然后利用这个定义,构建二叉树的套路很简单,先找到根节点,然后找到并递归构造左右子树即可)
二、刷题
1、最大二叉树
🔗654. 最大二叉树
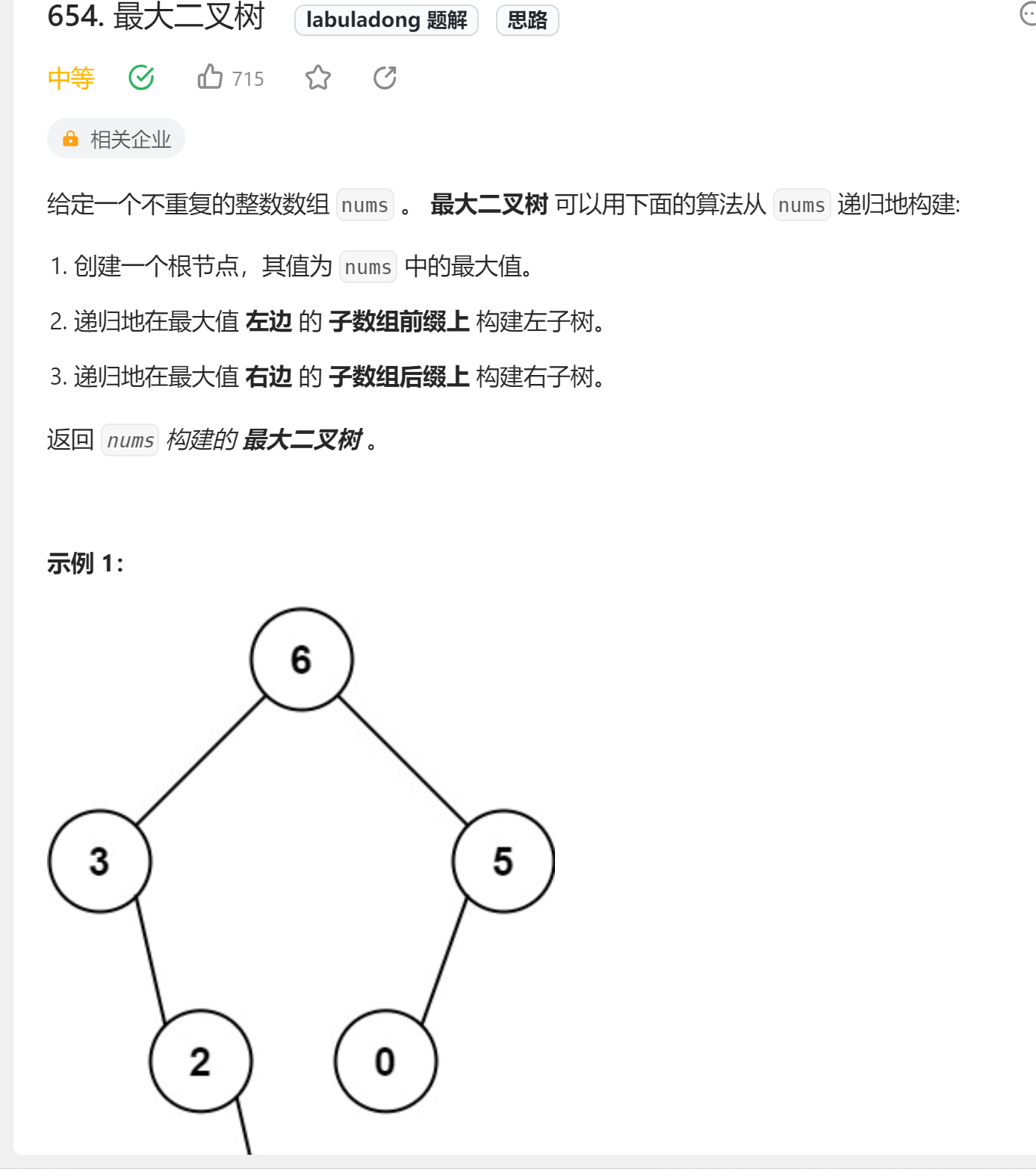
public TreeNode constructMaximumBinaryTree(int[] nums) {if(nums==null||nums.length==0){return null;}//1、找到最大元素,构造根节点int max = nums[0];int index = 0;for (int i = 1; i < nums.length; i++){if(nums[i] > max){index = i;max = nums[i];}}TreeNode root = new TreeNode(max);//左子树和右子树数组构造int[] numsLeft = Arrays.copyOfRange(nums, 0, index);int[] numsRight = Arrays.copyOfRange(nums,index+1, nums.length);root.left = constructMaximumBinaryTree(numsLeft);root.right = constructMaximumBinaryTree(numsRight);return root;}
2、从前序与中序遍历序列构造二叉树
🔗105. 从前序与中序遍历序列构造二叉树
-
👧🏻思路:
- 大的框架还是分解成子问题,这里定义一个递归函数:
build(递归函数的定义:给定二叉树前序遍历、中序遍历数组、前序数组起始坐标、前序数组末尾坐标、中序数组起始坐标、中序数组末尾坐标) - 在递归函数前序位置需要确定左子树两个数组的的四个坐标和右子树的四个坐标,核心是算出当前root在中序数组中的位置
rootIndex
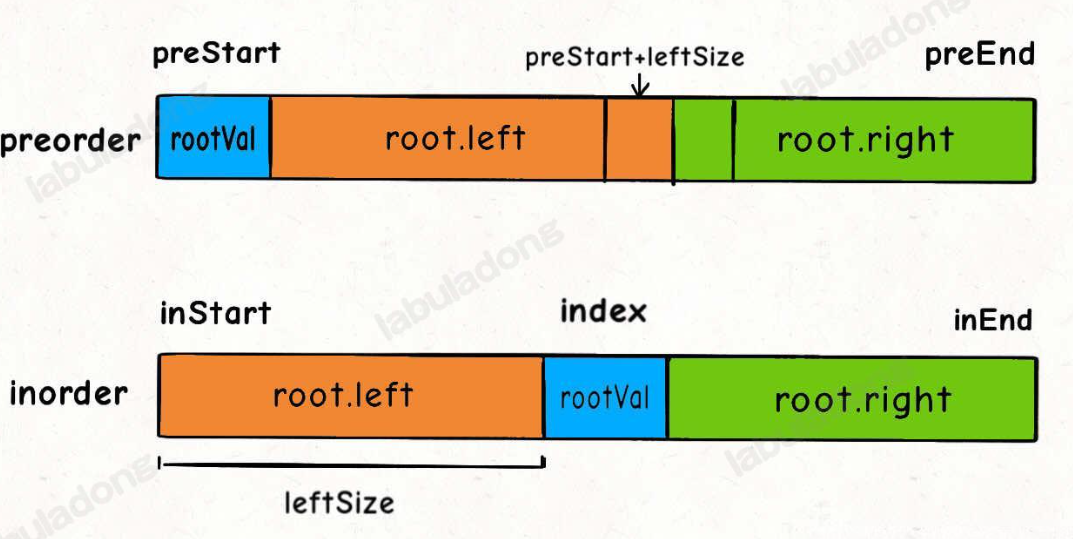
- 大的框架还是分解成子问题,这里定义一个递归函数:
-
🙇🏻♀️代码:
public TreeNode buildTree(int[] preorder, int[] inorder) {//递归函数的定义:给定二叉树前序遍历、中序遍历数组、前序数组起始坐标、前序数组末尾坐标、中序数组起始坐标、中序数组末尾坐标int pStart = 0;int pEnd = preorder.length-1;int iStart = 0;int iEnd = inorder.length-1;return build(preorder,inorder, pStart, pEnd, iStart, iEnd);}public TreeNode build(int[] preorder, int[] inorder, int pStart, int pEnd, int iStart, int iEnd){if(pStart > pEnd){return null;}//1、先在前序数组中找到根节点TreeNode root = new TreeNode(preorder[pStart]);//2、在中序数组中找到根节点,划分左右数组int rootIndex = -1;int leftSize = 0;for(int i = iStart; i <= iEnd; i++){if(inorder[i] == root.val){rootIndex = i;leftSize = i-iStart;break;}}root.left = build(preorder, inorder, pStart+1, pStart+leftSize, iStart ,rootIndex-1);root.right = build(preorder, inorder, pStart+leftSize+1, pEnd, rootIndex+1, iEnd);return root;}
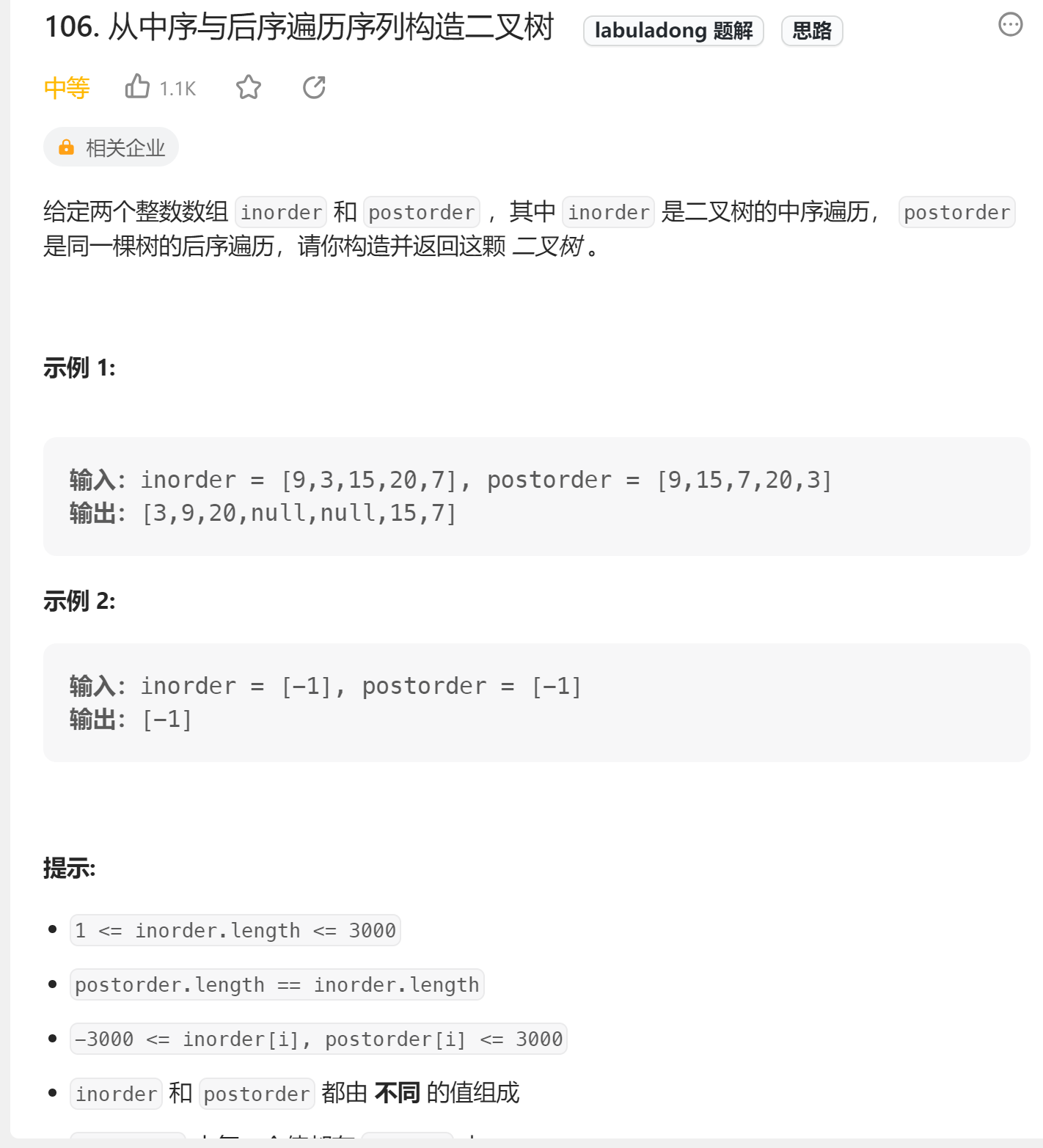
3、从中序与后序遍历序列构造二叉树
🔗106. 从中序与后序遍历序列构造二叉树
-
👧🏻思路:
- 同上,关键在于四个坐标的确定要准确
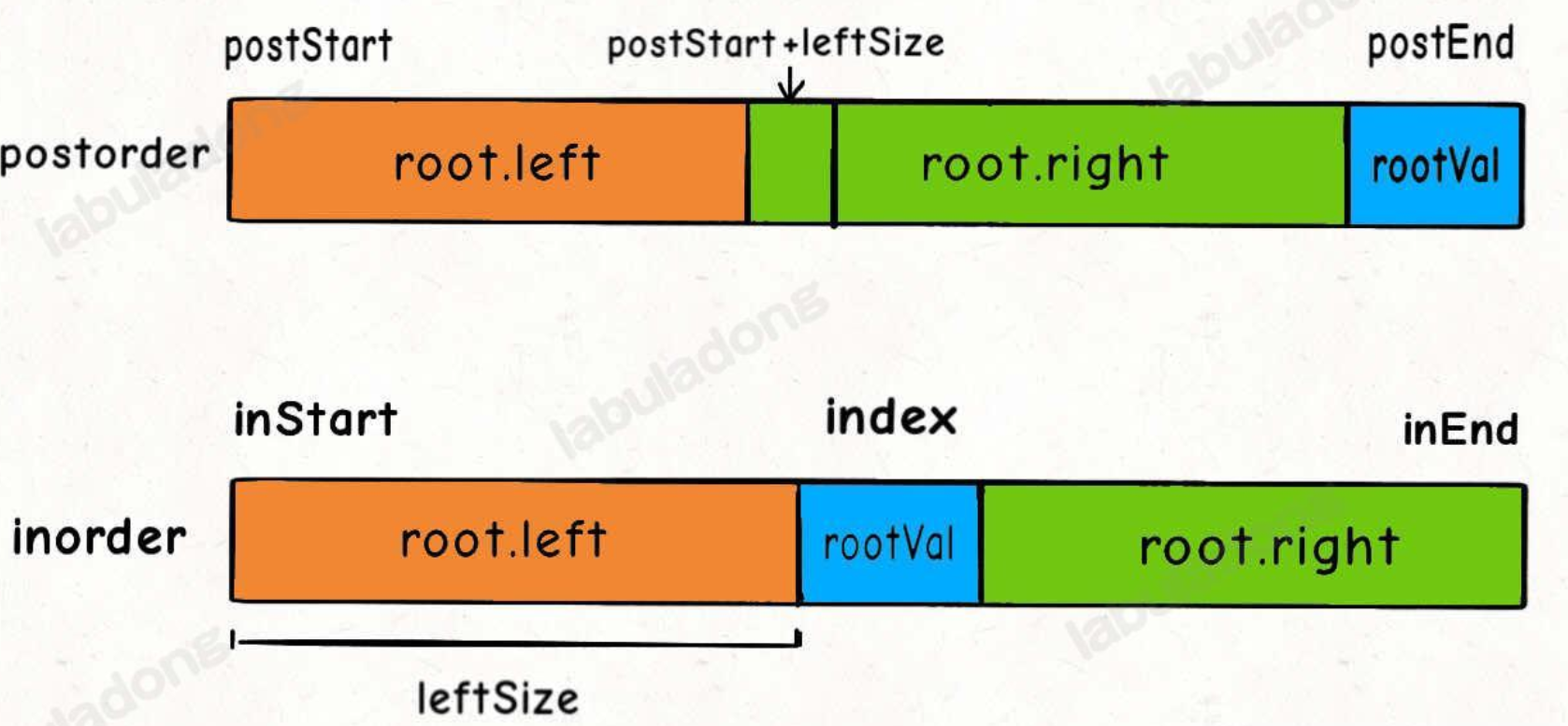
- 同上,关键在于四个坐标的确定要准确
-
🙇🏻♀️代码:
public TreeNode buildTree(int[] inorder, int[] postorder) {int inStart = 0;int inEnd = inorder.length -1;int posStart = 0;int posEnd = postorder.length - 1;return build(inorder, postorder, inStart, inEnd, posStart, posEnd);}public TreeNode build(int[] inorder, int[] postorder, int inStart, int inEnd, int posStart, int posEnd){if(posStart>posEnd){return null;}TreeNode root = new TreeNode(postorder[posEnd]);//得到根节点//找到根节点在中序数组中的位置int index = 0;int leftSize = 0;for(int i = inStart; i <= inEnd; i++ ){if(inorder[i] == root.val){index = i;leftSize = i - inStart;break;}}//*******构建左子树右子树 */root.left = build(inorder, postorder, inStart, index-1, posStart,posStart+leftSize -1);root.right = build(inorder, postorder, index+1, inEnd, posStart+leftSize,posEnd-1);return root;}
4、 根据前序和后序遍历构造二叉树
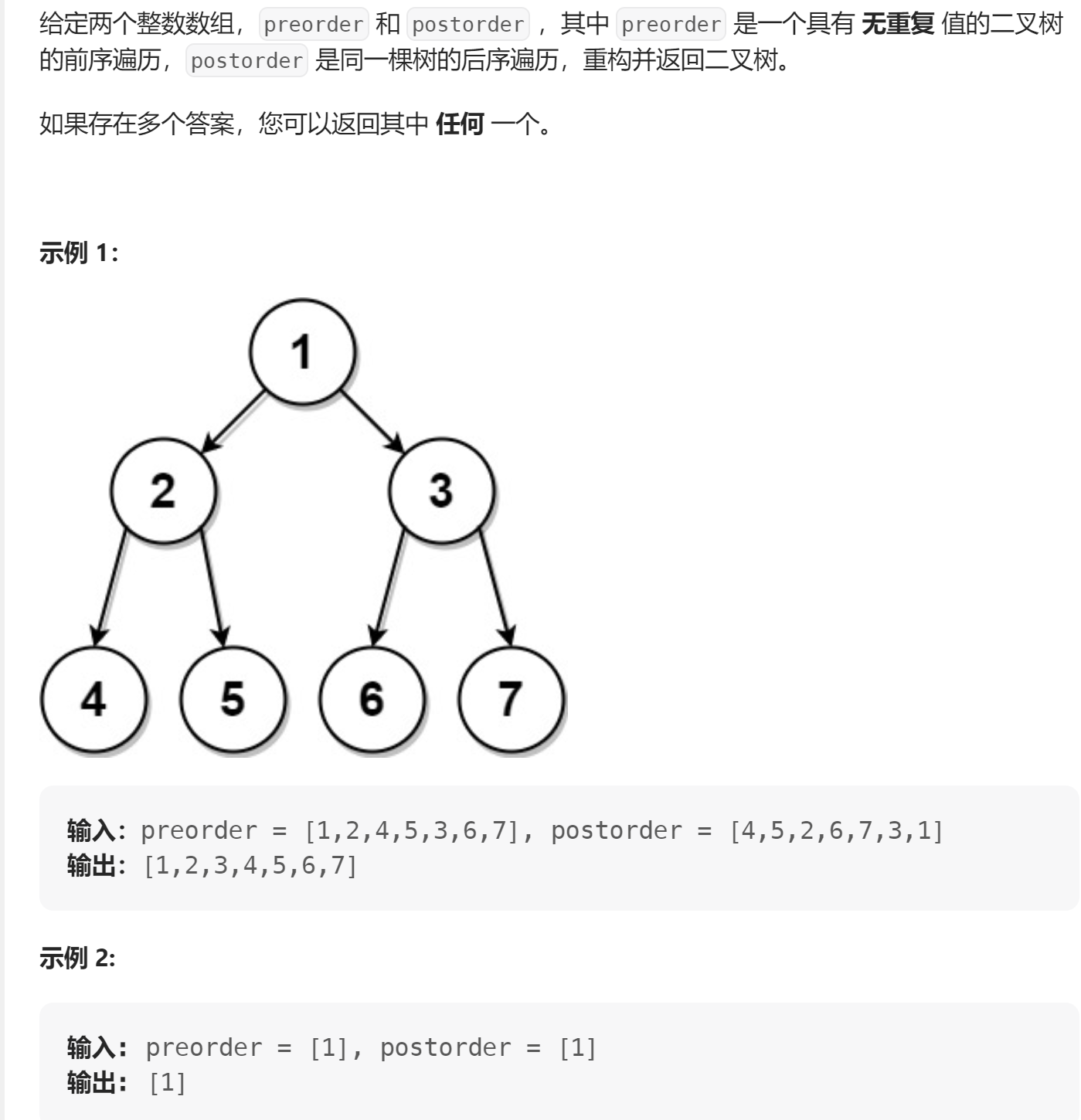
🔗889. 根据前序和后序遍历构造二叉树
- 👧🏻思路:
-
根据我们知道,只通过前序+后序是无法唯一构造一棵二叉树的。那么当然了,这题告诉我们有多个答案只用返回一个即可
-
前两个(前序+中序&&中序+后序)可以唯一确定是因为通过前序/后序数组可以在前序位置唯一确定根节点root,然后在中序数组中可以根据root分成左中序数组和右中序数组,所以是可以确定唯一一颗二叉树的。
-
而前序+后序按照这个思路其实也不是不行,因为前序和后序的数组划分是这样的:
🤔咦,根据上图,貌似前序和中序可以构造唯一二叉树呀
🙅🏻♀️不对,因为这里我们默认了一个大前提:root+1是left子树的跟,也就是默认了左子树至少有一个节点。但是实际上 ,左子树可能为空!——我们只是选取了其中一种可能情况而言。 -
🙋🏻构建思路
1. 首先将前序/后序遍历的第一个节点作为根节点root
2. 前序数组中,root后面相邻元素作为左子树的根节点(坐标记为preStartL=preStart+1);
3. 根据前序数组中的左子树根节点在后序数组中找到左子树的根节点:坐标记为posEndL
4. 从而求得左子树节点个数leftSize = posStartL - posStart + 1,将左右子树划分
5. 划分后即可确定左右子树的四个坐标点,带入递归函数分解成子问题即可
-

-
🙇🏻♀️代码:
public TreeNode constructFromPrePost(int[] preorder, int[] postorder) {int preStart = 0;int preEnd = preorder.length -1;int posStart = 0;int posEnd = postorder.length - 1;return build(preorder, postorder, preStart, preEnd, posStart, posEnd);}public TreeNode build(int[] preorder, int[] postorder, int preStart, int preEnd, int posStart, int posEnd){if (preStart > preEnd) {return null;}//****** */!注意,这种情况必须特判!*****if (preStart == preEnd) {return new TreeNode(preorder[preStart]);}//************************************* */TreeNode root = new TreeNode(preorder[preStart]);//1、得到根节点//2、key:求leftSizeint preStartL = preStart+1;//int posEndL = -1;//2.1:找左子树根节点在后序数组中的位置for(int i = posStart; i <= posEnd; i++ ){if(postorder[i] == preorder[preStartL]){posEndL = i;break;}}int leftSize = posEndL - posStart + 1;root.left = build(preorder, postorder, preStartL, preStartL + leftSize -1, posStart, posEndL);root.right = build(preorder, postorder, preStartL + leftSize, preEnd, posEndL + 1, posEnd -1 );return root;} -
🍊注意!:在上面代码重点标出部分,需要特判的原因是:我们在思路部分已经讲过,这种方法默认左子树至少有一个节点(一棵树至少有两个节点),而
preStart == preEnd并不满足这个大前提,所以需要特判!!
💐若有不懂的地方,欢迎随时在评论区or私信找瑶瑶子交流讨论🌺

-
Java岛冒险记【从小白到大佬之路】
-
LeetCode每日一题–进击大厂
-
Go语言核心编程
-
算法