同Kruskal算法一样,Prim算法也是最小生成树的算法,但与Kruskal算法有较大的差别。
Prim算法整体是通过“解锁” + “选中”的方式,点 -> 边 -> 点 -> 边。
因为是最小生成树,所以针对的也是无向图,所以可以随意选取一个点作为进入点,通过解锁这个点,可以获得从这个点出去的所有边,在通过这些边中权重最小的边解锁其他的点。如此反复。直到最小生成树的形成。
如图所示:
左侧为原始图,从a点出发(哪个点都可以,假设从a),解锁了a点(解锁的点画圈),并且解锁了从a点直接出发权重为1,2,9的三条边(边解锁为虚线),根据权重选择1的边(选择具体边改颜色)。并解锁了b点。
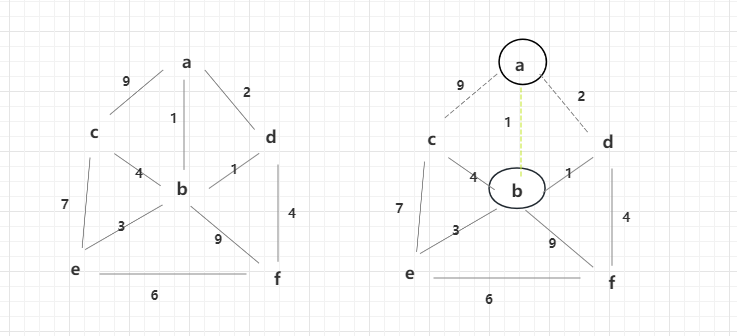
通过解锁的b点,可解锁权重1,3,4,9的边,此时bd边的权重最小为1,所以解锁了d的点。
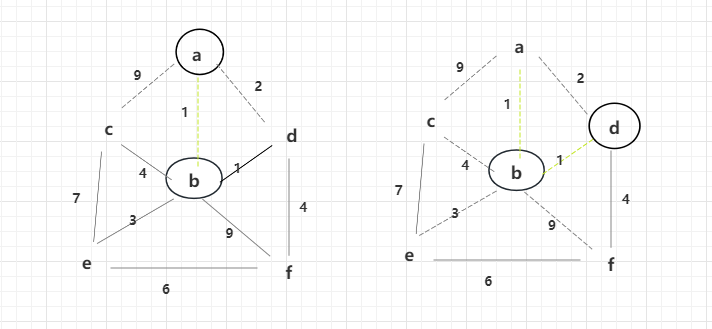
解锁d后,d直接出来的边4也会进行解锁。再次选择权重较小的为2,但是此时d已经解锁过了,所以不考虑2,再次选择be为3的边解锁。
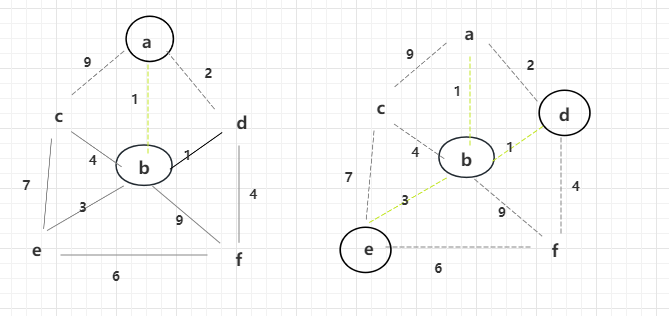
此时解锁后图形如上面所示,e点解锁后会解锁权重6、7的边。
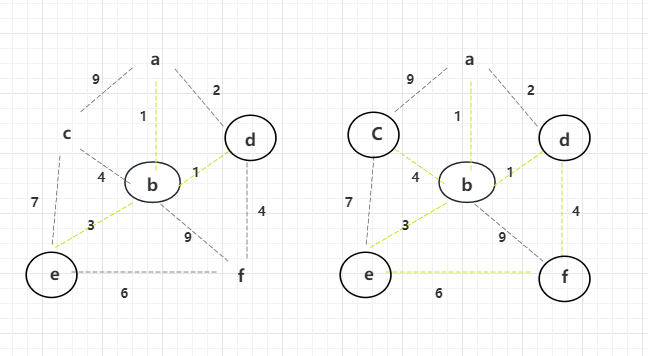
此时所有的边都已经解锁,选择权重小的边,并且不会形成环的点,进行解锁。
最终去掉所有没被选择的边,剩余的就是最小生成树。
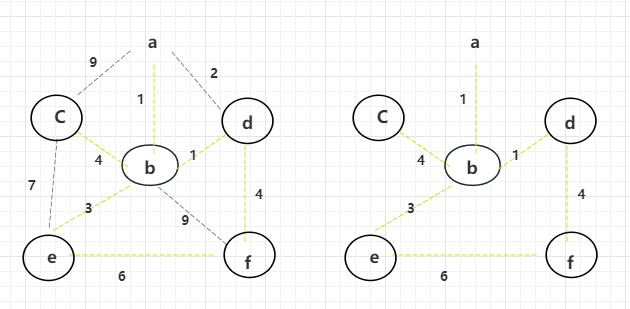
总结
- 最小生成树是要用最小距离接所有可达的点。
- 所以,随机的每一个点,在获取这个点所有的边中选取权重最小的 那一条边,组织起来就一定会是最小生成树组成的答案。
代码实现
基于上面图解是代码实现。点 > 边 -> 点 -> 边的解锁方式。
最外层的for循环可防“森林”。 a -> b c ->d e->f,a可以找到b,c可以找到d, e可以找到f。但是a c e之间互相没关系。
public static class EdgeComparator implements Comparator<Edge> {@Overridepublic int compare(Edge o1, Edge o2) {return o1.weight - o2.weight;}}public static Set<Edge> primMST(Graph graph) {//放入PriorityQueue中,并根据边的权重进行排序PriorityQueue<Edge> priorityQueue = new PriorityQueue<>(new EdgeComparator());//解锁的点Set<Node> setNodes = new HashSet<>();//构成最小生成树的所有边Set<Edge> result = new HashSet<>();//遍历图集中所有的点for (Node node : graph.nodes.values()) {//如果没解锁if (!setNodes.contains(node)) {setNodes.add(node);//将点的所有的边,放到PriorityQueue中排序for (Edge edge : node.edges) {priorityQueue.add(edge);}while (!priorityQueue.isEmpty()) {Edge edge = priorityQueue.poll();//获取到这个边连接的to点Node toNode = edge.to;if (!setNodes.contains(edge.to)) {//解锁to点setNodes.add(toNode);result.add(edge);//并且将to点所有的边也都放到Queue中for (Edge nextEdge : toNode.edges) {priorityQueue.add(nextEdge);}}}}//如果防森林,就不break break;}return result;}