节点不连续伽辽金方法在求解线性和非线性平流方程中的一维实现（Matlab代码实现）

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

💥1 概述

📚2 运行结果

🎉3 参考文献

🌈4 Matlab代码实现

💥1 概述

本文提出了节点不连续伽辽金方法在求解线性和非线性平流方程中的一维实现，无需任何滤波器或限幅器。本公式旨在向CFD从业者介绍该方法，因此它意味着可读性而不是非常有效的实施。

该方法的基本思想是将平流方程离散化为一维节点不连续伽辽金方程，然后使用迭代方法求解该方程。

在一维情况下，平流方程可以写为：

∂u/∂t + c ∂u/∂x = 0

其中，u是要求解的变量，t是时间，x是空间坐标，c是平流速度。

为了将平流方程离散化为节点不连续伽辽金方程，我们首先将时间和空间离散化为有限的网格点。然后，我们使用中心差分方法来近似平流方程中的导数项。具体来说，我们使用以下公式来近似时间导数和空间导数：

∂u/∂t ≈ (u_i^n+1 - u_i^n) / Δt

∂u/∂x ≈ (u_i+1^n - u_i-1^n) / (2Δx)

其中，u_i^n表示在第n个时间步长和第i个空间节点处的变量值，Δt是时间步长，Δx是空间步长。

将这些近似代入平流方程，我们得到节点不连续伽辽金方程：

(u_i^n+1 - u_i^n) / Δt + c (u_i+1^n - u_i-1^n) / (2Δx) = 0

为了求解该方程，我们使用迭代方法，如迭代法或牛顿法。迭代方法的基本思想是将方程转化为一个求根问题，并通过迭代逼近根的解。

总之，节点不连续伽辽金方法是一种求解线性和非线性平流方程的一维实现方法，它不需要滤波器或限幅器。然而，由于其可读性和实施的简单性，它可能不是非常高效的方法。

📚2 运行结果

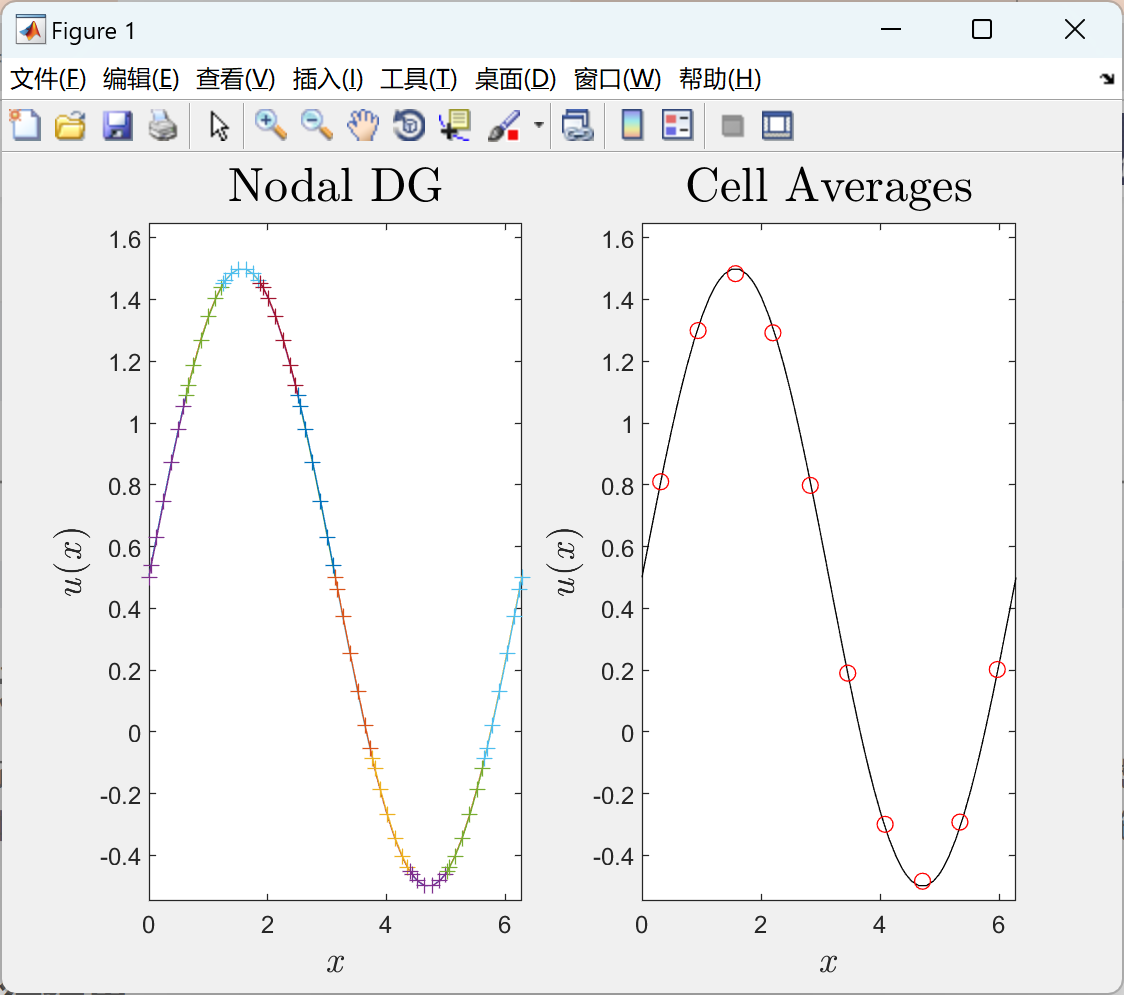
部分代码：

% Build 1d mesh
xgrid = mesh1d([0 2*pi],nE,'LGL',K);
dx = xgrid.elementSize; J = xgrid.Jacobian;
x = xgrid.nodeCoordinates; w = xgrid.weights';
xc = xgrid.elementCenter;

% Load DG tools
tool = DGtools(xgrid.solutionPoints);
V = tool.Vandermonde2;
invM = tool.nodalInvMassMatrix;
Dr = tool.nodalCoefDiffMatrix;

% Build Lift Operator
Emat = zeros(K+1,2); % array of element's shape function
Emat(1,1)=1; Emat(K+1,2)=1;
Lift = V*(V'*Emat);

% IC
u0 = IC(x,2);

% Set plot range
plotrange = [xgrid.range(1),xgrid.range(2),...
min(min(min(0.9*u0)),min(min(1.1*u0))),1.1*max(max(u0))];

%% Solver Loop

% Set initial time & load IC
t=0; u=u0; it=0;

% Using a 3rd Order 3-stage SSPRK time integration
while t < tEnd
uo = u;

% update time
dt = cfl*dx/max(max(abs(dflux(u)))); t = t+dt;

% iteration counter
it = it+1;

% 1st stage
dF = residual(u,flux,dflux,Lift,Dr);
u = uo-dt*dF/J;

% 2nd Stage
dF = residual(u,flux,dflux,Lift,Dr);
u = 0.75*uo+0.25*(u-dt*dF/J);

% 3rd stage
dF = residual(u,flux,dflux,Lift,Dr);
u = (uo+2*(u-dt*dF/J))/3;

% build cell averages
u_bar = w*u/2;

% Plot u
subplot(1,2,1); plot(x,u,x,u0,'-+'); axis(plotrange); grid off;
subplot(1,2,2); plot(xc,u_bar,'ro'); axis(plotrange); grid off;

%if rem(it,10) == 0
drawnow;
%end
end
%% Final Plot for IC 2
subplot(1,2,1); plot(x,u,x,u0,'-+'); axis(plotrange);
title('Nodal DG','interpreter','latex','FontSize',18);
xlabel('$\it{x}$','interpreter','latex','FontSize',14);
ylabel({'$\it{u(x)}$'},'interpreter','latex','FontSize',14);
subplot(1,2,2); plot(x,u0,'k-',xc,u_bar,'ro'); axis(plotrange);
title('Cell Averages','interpreter','latex','FontSize',18);
xlabel('$\it{x}$','interpreter','latex','FontSize',14);
ylabel({'$\it{u(x)}$'},'interpreter','latex','FontSize',14);