1.1 什么是OptaPlanner

每个组织都面临规划问题：为产品或服务提供有限的受约束的资源（员工、资产、时间和金钱）。OptaPlanner用来优化这种规划，以实现用更少的资源来做更多的业务。 这被称为Constraint Satisfaction Programming（约束规划，这是运筹学学科的一部分）。

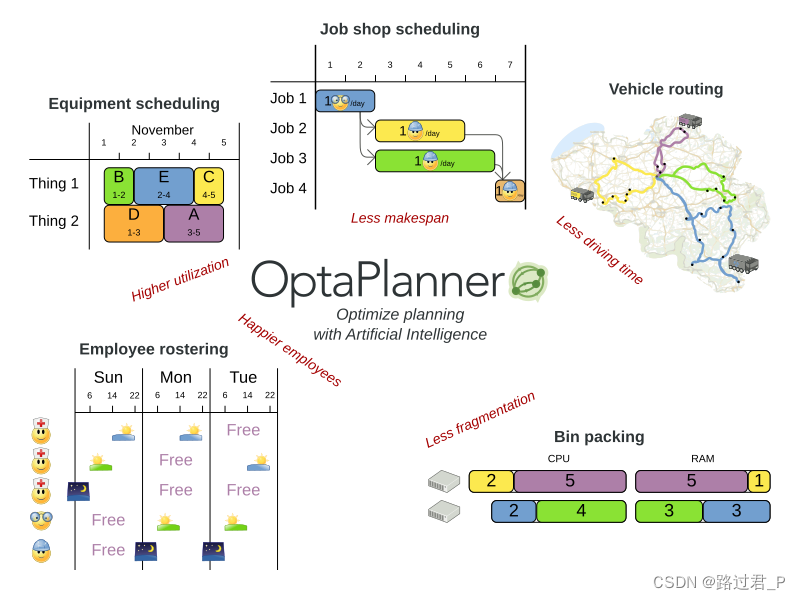
OptaPlanner 是一个轻量级、可嵌入的约束满足问题求解引擎，可优化规划问题。它适用的场景例如：

• 员工轮班排班：为护士、修理工等排班。
• 议程安排：安排会议，约会，维护工作，广告等。
• 教育方面的排班：安排学科，课程，考试，学术会议等。
• 车辆路线：利用已知的地图工具规划运输货物和/或乘客的车辆路线，这些路线可以经过多个目的地。
• 装箱问题：如何使用装箱、卡车、船舶和存储仓库装载物品，或者是云计算中如何跨计算机资源打包信息。
• 车间作业调度：汽车装配线规划、机器队列规划、劳动力任务规划等。
• 切割库存：在切割纸张、钢材、地毯等时最大限度地减少浪费。
• 体育日程安排：为足球联赛、棒球联赛规划比赛和训练时间表。
• 财务优化：投资组合优化、风险分散等。

1.2 什么是规划问题

规划问题存在一个基于有限资源和特定规则的最优解。最优解可以是任何数量的事务，例如：

• 利润最大化
• 环境影响最小化
• 员工和顾客满意度最大化

实现这些目标的能力取决于可用资源的数量，例如：

• 人员数量
• 时间
• 预算
• 实物资产（机械、车辆、计算机、建筑物等）

还必须考虑与这些资源相关的特定限制，例如一个人的工作小时数、他们使用某些机器的能力或设备之间的兼容性。

OptaPlanner可以帮助Java程序员有效地解决约束满足问题。它使用非常有效的得分计算，将优化启发式和元启发式算法结合在一起。

1.2.1 规划问题是NP-Complete还是NP-Hard问题

NP-Hard问题是指在多项式时间内无法解决的问题。这些问题通常是非常困难的，因为它们的解决需要大量的计算资源。NP-Hard问题的例子包括旅行推销员问题、分治问题等。
NP-Complete问题是指在多项式时间内可以解决，但在NP-Hard问题的解决过程中可以被解决的问题。这些问题的解决通常比NP-Hard问题的解决要快，但仍然需要大量的计算资源。NP-Complete问题的例子包括完全背包问题、分支界限问题等。

前面提到的所有场景都可能是NP-Complete或者NP-Hard的，也就是说：

• 在合理的时间内验证问题的给定解决方案很容易。
• 没有灵丹妙药可以在合理的时间内找到问题的最佳解决方案。（至少，世界上最聪明的计算机科学家还没有发现这样的灵丹妙药。 但是，如果他们找到一个适用于某个NP-Complete问题的解决方案，它将适用于每个NP-Complete问题。）

这意味着解决问题可能比你预期的要困难，因为常用的技术不足以解决问题：

• 蛮力算法（即使是再聪明的变体）将会耗费大量的时间
• 快速算法（例如在装箱问题中，先放入最大的物品）将得到远远偏离最优解的解决方案。

通过使用先进的优化算法，OptaPlanner 可以在合理的时间内为这类规划问题找到接近最优的解决方案。

1.2.2 规划问题存在约束（硬约束或软约束）

通常，规划问题存在至少两个级别的约束：

• 绝对不可破坏的（负面）硬约束。（例如，一名教师不能同时教授两节不同的课程。）
• 如果可以避免，就不应该破坏的（负面）软约束。（例如：某教师不喜欢在星期五的下午授课。）

某些问题也可能存在积极的约束：

• 如果可能的话，应该满足的（正向的）软约束。（例如，某教师喜欢在星期一的上午授课。）

某些基础问题（例如N皇后问题）只存在硬约束。某些问题存在三个或更多级别的约束，例如硬、中等、软约束。
这些约束定义了规划问题的得分计算（也称为适应度函数）。规划问题的每个解决方案都可以用得分评级。在 OptaPlanner 中，得分约束用面向对象的语言（例如Java代码）编写。这样的代码易于编写、灵活且可扩展。

1.2.3 规划问题存在巨大的搜索空间

规划问题有许多解决方案。 这些解决方案可划分为以下几类：

• 不考虑是否破坏任何约束的possible solution（可能方案）。规划问题往往存在大量这种毫无价值的解决方案。
• 不破坏任何负面硬约束的feasible solution（可行方案）。可行方案往往与可能方案数量相对。有时候没有可行方案。每一个可行方案都是可能方案
• 得分最高的optimal solution（最佳方案）。规划问题至少有一个最佳方案。即使没有可行方案，且最佳方案不可行的情况下也是如此。
• 在给定时间内找到的最高分的best solution（最优方案）。最优方案可能是可行的，如果时间充裕的话，它就是最佳方案。

与直觉相反，即使数据集很小，可能方案的数量也是巨大的（如果计算正确的话）。正如你在例子中看到的，大多数案例比已知宇宙中原子的数量（10^80）有更多的可能方案。由于没有找到最优解决方案的灵丹妙药，因此任何实现都必须评估一部分的可能方案。

OptaPlanner支持多种优化算法，可以有效地处理大量可能方案。 根据用例的不同，某些优化算法的性能优于其他算法，但无法提前判断。使用 OptaPlanner，只需几行XML或代码来修改求解器的配置，即可轻松切换优化算法。