文章内容来自DR_CAN关于傅里叶变换的视频,本篇文章提供了一些基础知识点,比如三角函数常用的导数、三角函数换算公式等。
文章全部链接:
基础知识点
Part1:三角函数系的正交性
Part2:T=2π的周期函数的傅里叶级数展开
Part3:周期为T=2L的函数展开
Part4:傅里叶级数的复数形式
Part5:从傅里叶级数推导傅里叶变换
总结
Part2: T = 2 π T = 2 \pi T=2π的周期函数的傅里叶级数展开
假设周期 T = 2 π T = 2 \pi T=2π,将一个周期函数展开为傅里叶级数如下:
f ( x ) = ∑ n = 1 ∞ ( a n c o s n x + b n s i n n x ) = a 0 2 + ∑ n = 1 ∞ ( a n c o s n x + b n s i n n x ) \begin{align} f(x) &= \sum_{n=1}^{\infty} (a_n cos nx + b_n sin nx) = \frac{a_0} {2} + \sum_{n = 1}^{\infty} \left ( a_n cos nx + b_n sin nx \right) & \end{align} f(x)=n=1∑∞(ancosnx+bnsinnx)=2a0+n=1∑∞(ancosnx+bnsinnx)
计算函数中的相关系数 a 0 a_0 a0、 a n a_n an、 b n b_n bn。
第一步,求解 a 0 a_0 a0,对 f ( x ) f(x) f(x)在 [ − π , π ] [-\pi, \pi] [−π,π]之间计算积分 ∫ − π π f ( x ) d x \int_{- \pi}^{\pi} f(x)dx ∫−ππf(x)dx,即为:
∫ − π π f ( x ) d x = a 0 2 ∫ − π π 1 d x + ∫ − π π ∑ n = 1 ∞ a n c o s n x d x + ∫ − π π ∑ n = 1 ∞ b n s i n n x d x \begin{align} & \int_{- \pi}^{\pi} f(x)dx = \frac{a_0}{2} \int_{- \pi}^{\pi} 1 dx + \int_{- \pi}^{\pi} \sum_{n = 1}^{\infty} a_n cos nx dx +\int_{- \pi}^{\pi} \sum_{n = 1}^{\infty} b_n sin nx dx & \end{align} ∫−ππf(x)dx=2a0∫−ππ1dx+∫−ππn=1∑∞ancosnxdx+∫−ππn=1∑∞bnsinnxdx
计算上式第2项
∫ − π π ∑ 1 ∞ a n c o s n x d x = ∫ − π π a 1 c o s x d x + ∫ − π π a 2 c o s 2 x d x + . . . + ∫ − π π a n c o s n x d x + . . . = a 1 ∫ − π π c o s x d x + a 2 ∫ − π π c o s 2 x d x + . . . + a n ∫ − π π c o s n x d x + . . . \begin{align} \int_{- \pi}^{\pi} \sum_1^{\infty} a_n cos nx dx &= \int_{- \pi}^{\pi} a_1 cos x dx + \int_{- \pi}^{\pi} a_2 cos 2x dx + ... + \int_{- \pi}^{\pi} a_n cos nx dx + ... \\ &= a_1 \int_{- \pi}^{\pi} cos x dx + a_2 \int_{- \pi}^{\pi} cos 2x dx + ... + a_n \int_{- \pi}^{\pi} cos nx dx + ... & \end{align} ∫−ππ1∑∞ancosnxdx=∫−ππa1cosxdx+∫−ππa2cos2xdx+...+∫−ππancosnxdx+...=a1∫−ππcosxdx+a2∫−ππcos2xdx+...+an∫−ππcosnxdx+...
根据三角函数的正交性, ∫ − π π ∑ n = 1 ∞ a n c o s n x d x = 0 \int_{- \pi}^{\pi} \sum_{n = 1}^{\infty} a_n cos nx dx = 0 ∫−ππ∑n=1∞ancosnxdx=0
计算第3项
∫ − π π ∑ 1 ∞ b n s i n n x d x = ∫ − π π b 1 s i n x d x + ∫ − π π b 2 s i n 2 x d x + . . . + ∫ − π π b n s i n n x d x + . . . = b 1 ∫ − π π s i n x d x + b 2 ∫ − π π s i n 2 x d x + . . . + b n ∫ − π π s i n n x d x + . . . \begin{align} \int_{- \pi}^{\pi} \sum_1^{\infty} b_n sin nx dx &= \int_{- \pi}^{\pi} b_1 sin x dx + \int_{- \pi}^{\pi} b_2 sin 2x dx + ... + \int_{- \pi}^{\pi} b_n sin nx dx + ... \\ &= b_1 \int_{- \pi}^{\pi} sin x dx + b_2 \int_{- \pi}^{\pi} sin 2x dx + ... + b_n \int_{- \pi}^{\pi} sin nx dx + ... &\end{align} ∫−ππ1∑∞bnsinnxdx=∫−ππb1sinxdx+∫−ππb2sin2xdx+...+∫−ππbnsinnxdx+...=b1∫−ππsinxdx+b2∫−ππsin2xdx+...+bn∫−ππsinnxdx+...
根据三角函数正交性, ∫ − π π ∑ n = 1 ∞ b n s i n n x d x = 0 \int_{- \pi}^{\pi} \sum_{n = 1}^{\infty} b_n sin nx dx = 0 ∫−ππ∑n=1∞bnsinnxdx=0
那么 ∫ − π π f ( x ) d x = a 0 2 ∫ − π π 1 d x = a 0 2 x ∣ − π π = a 0 2 2 π = π a 0 \int_{- \pi}^{\pi} f(x)dx = \frac{a_0}{2} \int_{- \pi}^{\pi} 1 dx = \frac{a_0}{2} x|_{- \pi}^{\pi} = \frac{a_0}{2} 2 \pi = \pi a_0 ∫−ππf(x)dx=2a0∫−ππ1dx=2a0x∣−ππ=2a02π=πa0,计算求得:
a 0 = 1 π ∫ − π π f ( x ) d x \begin{align} & a_0 = \frac{1}{\pi}\int_{- \pi}^{\pi} f(x)dx & \end{align} a0=π1∫−ππf(x)dx
第二步,计算 a n a_n an,等号两边同时乘以 c o s m x cos mx cosmx,然后在 [ − π , π ] [-\pi, \pi] [−π,π]区间内求积分。如下:
∫ − π π f ( x ) c o s m x d x = a 0 2 ∫ − π π c o s m x d x + ∫ − π π ∑ n = 1 ∞ a n c o s n x c o s m x d x + ∫ − π π ∑ n = 1 ∞ b n s i n n x c o s m x d x \begin{align} & \int_{- \pi}^{\pi} f(x) cos mx dx = \frac{a_0}{2} \int_{- \pi}^{\pi} cosmx dx + \int_{- \pi}^{\pi} \sum_{n = 1}^{\infty} a_n cos nx cos mx dx + \int_{- \pi}^{\pi} \sum_{n = 1}^{\infty} b_n sin nx cos mx dx & \end{align} ∫−ππf(x)cosmxdx=2a0∫−ππcosmxdx+∫−ππn=1∑∞ancosnxcosmxdx+∫−ππn=1∑∞bnsinnxcosmxdx
计算第一项结果为0
a 0 2 ∫ − π π c o s m x d x = a 0 2 ∫ − π π c o s 0 x c o s m x d x = 0 \begin{align} &\frac{a_0}{2} \int_{- \pi}^{\pi} cosmx dx = \frac{a_0}{2} \int_{- \pi}^{\pi} cos 0x cosmx dx = 0 & \end{align} 2a0∫−ππcosmxdx=2a0∫−ππcos0xcosmxdx=0
计算第二项
∫ − π π ∑ n = 1 ∞ a n c o s n x c o s m x d x = ∫ − π π a 1 c o s x c o s m x d x + ∫ − π π a 2 c o s 2 x c o s m x d x + . . . + ∫ − π π a n c o s n x c o s m x d x + . . . = a 1 ∫ − π π c o s x c o s m x d x + a 2 ∫ − π π c o s 2 x c o s m x d x + . . . + a n ∫ − π π c o s n x c o s m x d x + . . . \begin{align} \int_{- \pi}^{\pi} \sum_{n = 1}^{\infty} a_n cos nx cos mx dx &= \int_{- \pi}^{\pi} a_1 cos x cos mx dx + \int_{- \pi}^{\pi} a_2 cos 2x cos mx dx + ... + \int_{- \pi}^{\pi} a_n cos nx cos mx dx + ... \\ & = a_1 \int_{- \pi}^{\pi} cos x cos mx dx + a_2 \int_{- \pi}^{\pi} cos 2x cos mx dx + ... + a_n \int_{- \pi}^{\pi} cos nx cos mx dx + ... & \end{align} ∫−ππn=1∑∞ancosnxcosmxdx=∫−ππa1cosxcosmxdx+∫−ππa2cos2xcosmxdx+...+∫−ππancosnxcosmxdx+...=a1∫−ππcosxcosmxdx+a2∫−ππcos2xcosmxdx+...+an∫−ππcosnxcosmxdx+...
当 m ≠ n m \ne n m=n时
a n ∫ − π π c o s n x c o s m x d x = 0 \begin{align} & a_n \int_{- \pi}^{\pi} cos nx cos mx dx = 0 & \end{align} an∫−ππcosnxcosmxdx=0
当 m = n m=n m=n时,根据三角函数平方公式可得 ∫ − π π c o s n x c o s n x d x = 1 2 [ ∫ − π π 1 d x + ∫ − π π c o s 2 n x d x ] = π \int_{- \pi}^{\pi} cos nx cos nx dx = \frac{1}{2} \left [\int_{- \pi}^{\pi}1dx + \int_{- \pi}^{\pi}cos 2nxdx \right] = \pi ∫−ππcosnxcosnxdx=21[∫−ππ1dx+∫−ππcos2nxdx]=π,该项只会保留当 m = n m=n m=n时的结果,即:
∫ − π π ∑ n = 1 ∞ a n c o s n x c o s m x d x = ∫ − π π a n c o s n x c o s n x d x = π a n \begin{align} & \int_{- \pi}^{\pi} \sum_{n = 1}^{\infty} a_n cos nx cos mx dx = \int_{- \pi}^{\pi} a_n cos nx cos nx dx = \pi a_n & \end{align} ∫−ππn=1∑∞ancosnxcosmxdx=∫−ππancosnxcosnxdx=πan
计算第三项
∫ − π π ∑ n = 1 ∞ b n s i n n x c o s m x d x = ∫ − π π a 1 s i n x c o s m x d x + ∫ − π π a 2 s i n 2 x c o s m x d x + . . . + ∫ − π π a n s i n n x c o s m x d x + . . . = a 1 ∫ − π π s i n x c o s m x d x + a 2 ∫ − π π s i n 2 x c o s m x d x + . . . + a n ∫ − π π s i n n x c o s m x d x + . . . \begin{align} \int_{- \pi}^{\pi} \sum_{n = 1}^{\infty} b_n sin nx cos mx dx &= \int_{- \pi}^{\pi} a_1 sin x cos mx dx + \int_{- \pi}^{\pi} a_2 sin 2x cos mx dx + ... + \int_{- \pi}^{\pi} a_n sin nx cos mx dx + ... \\ & = a_1 \int_{- \pi}^{\pi} sin x cos mx dx + a_2 \int_{- \pi}^{\pi} sin 2x cos mx dx + ... + a_n \int_{- \pi}^{\pi} sin nx cos mx dx + ... & \end{align} ∫−ππn=1∑∞bnsinnxcosmxdx=∫−ππa1sinxcosmxdx+∫−ππa2sin2xcosmxdx+...+∫−ππansinnxcosmxdx+...=a1∫−ππsinxcosmxdx+a2∫−ππsin2xcosmxdx+...+an∫−ππsinnxcosmxdx+...
由正交性可得第三项为0:
∫ − π π ∑ n = 1 ∞ b n s i n n x c o s m x d x = 0 \begin{align} &\int_{- \pi}^{\pi} \sum_{n = 1}^{\infty} b_n sin nx cos mx dx = 0 & \end{align} ∫−ππn=1∑∞bnsinnxcosmxdx=0
那么就有:
∫ − π π f ( x ) c o s n x d x = ∫ − π π ∑ n = 1 ∞ a n c o s n x c o s m x d x = π a n ⇒ a n = 1 π ∫ − π π f ( x ) c o s n x d x \begin{align} & \int_{- \pi}^{\pi} f(x) cos nx dx = \int_{- \pi}^{\pi} \sum_{n = 1}^{\infty} a_n cos nx cos mx dx = \pi a_n \\ & \Rightarrow \\ & a_n = \frac{1}{\pi} \int_{- \pi}^{\pi} f(x) cos nx dx &\end{align} ∫−ππf(x)cosnxdx=∫−ππn=1∑∞ancosnxcosmxdx=πan⇒an=π1∫−ππf(x)cosnxdx
第三步,计算 b n b_n bn,等式两边乘以 s i n m x sin mx sinmx,然后在区间 [ − π , π ] [-\pi, \pi] [−π,π]之间计算积分,如下:
∫ − π π f ( x ) s i n m x d x = a 0 2 ∫ − π π s i n m x d x + ∫ − π π ∑ n = 1 ∞ a n c o s n x s i n m x d x + ∫ − π π ∑ n = 1 ∞ b n s i n n x s i n m x d x \begin{align} & \int_{- \pi}^{\pi} f(x) sin mx dx = \frac{a_0}{2} \int_{- \pi}^{\pi} sin mx dx + \int_{- \pi}^{\pi} \sum_{n = 1}^{\infty} a_n cos nx sin mx dx + \int_{- \pi}^{\pi} \sum_{n = 1}^{\infty} b_n sin nx sin mx dx & \end{align} ∫−ππf(x)sinmxdx=2a0∫−ππsinmxdx+∫−ππn=1∑∞ancosnxsinmxdx+∫−ππn=1∑∞bnsinnxsinmxdx
计算第一项为0:
a 0 2 ∫ − π π s i n m x d x = a 0 2 ∫ − π π c o s 0 x s i n m x d x = 0 \begin{align} &\frac{a_0}{2} \int_{- \pi}^{\pi} sin mx dx = \frac{a_0}{2} \int_{- \pi}^{\pi} cos 0x sin mx dx = 0 & \end{align} 2a0∫−ππsinmxdx=2a0∫−ππcos0xsinmxdx=0
计算第二项为0:
∫ − π π ∑ n = 1 ∞ a n c o s n x s i n m x d x = ∫ − π π a 1 c o s x s i n m x d x + ∫ − π π a 2 c o s 2 x s i n m x d x + . . . + ∫ − π π a n c o s n x s i n m x d x + . . . = a 1 ∫ − π π c o s x s i n m x d x + a 2 ∫ − π π c o s 2 x s i n m x d x + . . . + a n ∫ − π π c o s n x s i n m x d x + . . . = 0 \begin{align} \int_{- \pi}^{\pi} \sum_{n = 1}^{\infty} a_n cos nx sin mx dx &= \int_{- \pi}^{\pi} a_1 cos x sin mx dx + \int_{- \pi}^{\pi} a_2 cos 2x sin mx dx + ... + \int_{- \pi}^{\pi} a_n cos nx sin mx dx + ... \\ & = a_1 \int_{- \pi}^{\pi} cos x sin mx dx + a_2 \int_{- \pi}^{\pi} cos 2x sin mx dx + ... + a_n \int_{- \pi}^{\pi} cos nx sin mx dx + ... \\ & = 0 & \end{align} ∫−ππn=1∑∞ancosnxsinmxdx=∫−ππa1cosxsinmxdx+∫−ππa2cos2xsinmxdx+...+∫−ππancosnxsinmxdx+...=a1∫−ππcosxsinmxdx+a2∫−ππcos2xsinmxdx+...+an∫−ππcosnxsinmxdx+...=0
计算第三项
∫ − π π ∑ n = 1 ∞ b n s i n n x s i n m x d x = ∫ − π π b 1 s i n x s i n m x d x + ∫ − π π b 2 s i n 2 x s i n m x d x + . . . + ∫ − π π b n s i n n x s i n m x d x + . . . = b 1 ∫ − π π s i n x s i n m x d x + b 2 ∫ − π π s i n 2 x s i n m x d x + . . . + b n ∫ − π π s i n n x s i n m x d x + . . . \begin{align} \int_{- \pi}^{\pi} \sum_{n = 1}^{\infty} b_n sin nx sin mx dx &= \int_{- \pi}^{\pi} b_1 sin x sin mx dx + \int_{- \pi}^{\pi} b_2 sin 2x sin mx dx + ... + \int_{- \pi}^{\pi} b_n sin nx sin mx dx + ... \\ & = b_1 \int_{- \pi}^{\pi} sin x sin mx dx + b_2 \int_{- \pi}^{\pi} sin 2x sin mx dx + ... + b_n \int_{- \pi}^{\pi} sin nx sin mx dx + ... & \end{align} ∫−ππn=1∑∞bnsinnxsinmxdx=∫−ππb1sinxsinmxdx+∫−ππb2sin2xsinmxdx+...+∫−ππbnsinnxsinmxdx+...=b1∫−ππsinxsinmxdx+b2∫−ππsin2xsinmxdx+...+bn∫−ππsinnxsinmxdx+...
当 m ≠ n m \ne n m=n时
b n ∫ − π π s i n n x s i n m x d x = 0 \begin{align} & b_n \int_{- \pi}^{\pi} sin nx sin mx dx = 0 & \end{align} bn∫−ππsinnxsinmxdx=0
当 m = n m=n m=n时,根据三角函数平方公式可得 ∫ − π π s i n n x s i n n x d x = 1 2 [ ∫ − π π 1 d x − ∫ − π π c o s 2 n x d x ] = π \int_{- \pi}^{\pi} sin nx sin nx dx = \frac{1}{2} \left [\int_{- \pi}^{\pi}1dx - \int_{- \pi}^{\pi}cos 2nxdx \right] = \pi ∫−ππsinnxsinnxdx=21[∫−ππ1dx−∫−ππcos2nxdx]=π,该项只会保留当 m = n m=n m=n时的结果,即:
∫ − π π ∑ n = 1 ∞ b n s i n n x s i n m x d x = ∫ − π π b n s i n ( n x ) s i n ( n x ) d x = π b n \begin{align} & \int_{- \pi}^{\pi} \sum_{n = 1}^{\infty} b_n sin nx sin mx dx = \int_{- \pi}^{\pi} b_n sin (nx) sin (nx) dx = \pi b_n & \end{align} ∫−ππn=1∑∞bnsinnxsinmxdx=∫−ππbnsin(nx)sin(nx)dx=πbn
那么就有:
∫ − π π f ( x ) s i n n x d x = ∫ − π π ∑ n = 1 ∞ b n s i n n x s i n m x d x = π b n ⇒ b n = 1 π ∫ − π π f ( x ) s i n n x d x \begin{align} & \int_{- \pi}^{\pi} f(x) sin nx dx = \int_{- \pi}^{\pi} \sum_{n = 1}^{\infty} b_n sin nx sin mx dx = \pi b_n \\ & \Rightarrow \\ & b_n = \frac{1}{\pi} \int_{- \pi}^{\pi} f(x) sin nx dx &\end{align} ∫−ππf(x)sinnxdx=∫−ππn=1∑∞bnsinnxsinmxdx=πbn⇒bn=π1∫−ππf(x)sinnxdx
综上,可以得出,对于一个周期 T = 2 π T=2 \pi T=2π的周期函数,其傅里叶级数为:
f ( x ) = a 0 2 + ∑ n = 1 ∞ ( a n c o s n x + b n s i n n x ) 其中 , a 0 = 1 π ∫ − π π f ( x ) d x a n = 1 π ∫ − π π f ( x ) c o s n x d x b n = 1 π ∫ − π π f ( x ) s i n n x d x \begin{align} & f(x) = \frac{a_0} {2} + \sum_{n = 1}^{\infty} \left ( a_n cos nx + b_n sin nx \right) \\ & 其中, \\ & a_0 = \frac{1}{\pi}\int_{- \pi}^{\pi} f(x)dx \\ & a_n = \frac{1}{\pi} \int_{- \pi}^{\pi} f(x) cos nx dx \\ & b_n = \frac{1}{\pi} \int_{- \pi}^{\pi} f(x) sin nx dx &\end{align} f(x)=2a0+n=1∑∞(ancosnx+bnsinnx)其中,a0=π1∫−ππf(x)dxan=π1∫−ππf(x)cosnxdxbn=π1∫−ππf(x)sinnxdx
Part3:周期为 2 L 2L 2L的函数展开
对于一个 T = 2 L T=2L T=2L的周期函数 f ( t ) = f ( t + 2 L ) f(t) = f(t+2L) f(t)=f(t+2L) ,展开傅里叶级数。
换元法令 x = π L t x = \frac{\pi}{L} t x=Lπt,那么 t = L π x t = \frac{L}{\pi} x t=πLx,代入到 f ( t ) f(t) f(t)
f ( t ) = f ( L π x ) \begin{align} & f(t) = f(\frac{L}{\pi}x) & \end{align} f(t)=f(πLx)
令 g ( x ) = f ( t ) = f ( L π x ) g(x) = f(t) = f(\frac{L}{\pi}x) g(x)=f(t)=f(πLx)。
有 x x x与 t t t、 f ( t ) = g ( x ) f(t)=g(x) f(t)=g(x)的换算关系可以得到:
( t = − L ⇔ x = − π ) ⇒ f ( − L ) = g ( − π ) (t=-L \Leftrightarrow x=-\pi) \Rightarrow f(-L) = g(-\pi) (t=−L⇔x=−π)⇒f(−L)=g(−π)
( t = L ⇔ x = π ) ⇒ f ( L ) = g ( π ) (t=L \Leftrightarrow x=\pi) \Rightarrow f(L) = g(\pi) (t=L⇔x=π)⇒f(L)=g(π)
( t = 3 L ⇔ x = 3 π ) ⇒ f ( 3 L ) = g ( 3 π ) (t=3L \Leftrightarrow x= 3\pi) \Rightarrow f(3L) = g(3 \pi) (t=3L⇔x=3π)⇒f(3L)=g(3π)
. . . ... ...
因为 f ( t ) f(t) f(t)是一个周期为 2 L 2L 2L函数,有 f ( − L ) = f ( L ) = f ( 3 L ) . . . f(-L) = f(L) = f(3L)... f(−L)=f(L)=f(3L)...,那么就有 g ( − π ) = g ( π ) = g ( 3 π ) . . . g(-\pi) = g( \pi) = g(3 \pi)... g(−π)=g(π)=g(3π)...,可以看出 g ( x ) g(x) g(x)是一个周期为 2 π 2 \pi 2π的周期函数。
展开 g ( x ) g(x) g(x)傅里叶级数为:
g ( x ) = a 0 2 + ∑ n = 1 ∞ ( a n c o s n x + b n s i n n x ) 其中 , a 0 = 1 π ∫ − π π g ( x ) d x a n = 1 π ∫ − π π g ( x ) c o s n x d x b n = 1 π ∫ − π π g ( x ) s i n n x d x \begin{align} & g(x) = \frac{a_0} {2} + \sum_{n = 1}^{\infty} \left ( a_n cos nx + b_n sin nx \right) \\ & 其中, \\ & a_0 = \frac{1}{\pi}\int_{- \pi}^{\pi} g(x)dx \\ & a_n = \frac{1}{\pi} \int_{- \pi}^{\pi} g(x) cos nx dx \\ & b_n = \frac{1}{\pi} \int_{- \pi}^{\pi} g(x) sin nx dx &\end{align} g(x)=2a0+n=1∑∞(ancosnx+bnsinnx)其中,a0=π1∫−ππg(x)dxan=π1∫−ππg(x)cosnxdxbn=π1∫−ππg(x)sinnxdx
将 x = π L t x = \frac{\pi}{L}t x=Lπt代入,有:
c o s n x = c o s n π L t s i n n x = s i n n π L t g ( x ) = f ( t ) ∫ − π π d x = ∫ − L L d π L t = π L ∫ − L L d t 1 π ∫ − π π d x = 1 π ∫ − L L d π L t = 1 π π L ∫ − L L d t = 1 L ∫ − L L d t \begin{align} cos nx & = cos \frac{n \pi}{L}t \\ sin nx & = sin \frac{n \pi}{L}t \\ g(x) & = f(t) \\ \int_{-\pi}^{\pi} dx & = \int_{-L}^{L} d \frac{\pi}{L}t = \frac{\pi}{L} \int_{-L}^{L}dt \\ \frac{1}{\pi} \int_{-\pi}^{\pi} dx & = \frac{1}{\pi} \int_{-L}^{L} d \frac{\pi}{L}t = \frac{1}{\pi} \frac{\pi}{L} \int_{-L}^{L}dt = \frac{1}{L} \int_{-L}^{L}dt \\ &\end{align} cosnxsinnxg(x)∫−ππdxπ1∫−ππdx=cosLnπt=sinLnπt=f(t)=∫−LLdLπt=Lπ∫−LLdt=π1∫−LLdLπt=π1Lπ∫−LLdt=L1∫−LLdt
代入展开函数有:
f ( t ) = a 0 2 + ∑ n = 1 ∞ ( a n c o s n π L t + b n s i n n π L t ) 其中 , a 0 = 1 L ∫ − L L f ( t ) d x a n = 1 L ∫ − L L f ( t ) c o s n π L t d x b n = 1 L ∫ − L L f ( t ) s i n n π L t d x \begin{align} f(t) &= \frac{a_0} {2} + \sum_{n = 1}^{\infty} \left ( a_n cos \frac{n \pi}{L}t + b_n sin \frac{n \pi}{L}t \right) \\ & 其中, \\ a_0 &= \frac{1}{L}\int_{- L}^{L} f(t)dx \\ a_n &= \frac{1}{L} \int_{- L}^{L} f(t) cos \frac{n \pi}{L}t dx \\ b_n &= \frac{1}{L} \int_{- L}^{L} f(t) sin \frac{n \pi}{L}t dx &\end{align} f(t)a0anbn=2a0+n=1∑∞(ancosLnπt+bnsinLnπt)其中,=L1∫−LLf(t)dx=L1∫−LLf(t)cosLnπtdx=L1∫−LLf(t)sinLnπtdx
在工程中, t t t从 0 0 0开始,周期 T = 2 L T = 2L T=2L,令 ω = π L = 2 π T \omega = \frac{\pi}{L} = \frac{2 \pi}{T} ω=Lπ=T2π,有 L = π ω L = \frac{\pi}{\omega} L=ωπ
对于周期函数
∫ − L L d t = ∫ 0 2 L d t = ∫ 0 T d t \begin{align} & \int_{-L}^{L} dt = \int_{0}^{2L} dt = \int_{0}^{T} dt &\end{align} ∫−LLdt=∫02Ldt=∫0Tdt
代入上面的展开函数就得到,对于 T = 2 L T=2L T=2L的周期函数,其傅里叶级数展开如下:
f ( t ) = a 0 2 + ∑ n = 1 ∞ ( a n c o s n ω t + b n s i n n ω t ) 其中 , a 0 = 1 L ∫ − L L f ( t ) d x a n = 1 L ∫ − L L f ( t ) c o s n ω t d x b n = 1 L ∫ − L L f ( t ) s i n n ω t d x \begin{align} & f(t) = \frac{a_0} {2} + \sum_{n = 1}^{\infty} \left ( a_n cos n \omega t + b_n sin n \omega t \right) \\ & 其中, \\ & a_0 = \frac{1}{L}\int_{- L}^{L} f(t)dx \\ & a_n = \frac{1}{L} \int_{- L}^{L} f(t) cos n \omega t dx \\ & b_n = \frac{1}{L} \int_{- L}^{L} f(t) sin n \omega t dx &\end{align} f(t)=2a0+n=1∑∞(ancosnωt+bnsinnωt)其中,a0=L1∫−LLf(t)dxan=L1∫−LLf(t)cosnωtdxbn=L1∫−LLf(t)sinnωtdx
原视频博主提供了一个示例,计算如下图所示的周期函数的傅里叶展开。
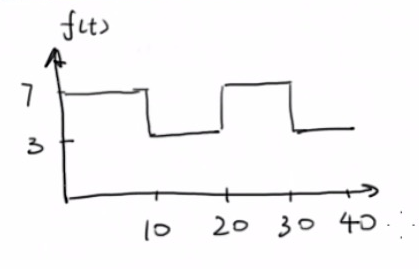
解:
由上图知道周期 T = 2 L = 20 T= 2L = 20 T=2L=20,令 ω = π L = π 10 \omega = \frac{\pi} {L} = \frac{\pi}{10} ω=Lπ=10π。根据上面得到的结论,上图的傅里叶级数展开函数为:
f ( t ) = a 0 2 + ∑ n = 1 ∞ ( a n c o s n ω t + b n s i n n ω t ) ,其中 L = 10 a 0 = 1 L ∫ − L L f ( t ) d x a n = 1 L ∫ − L L f ( t ) c o s n ω t d x b n = 1 L ∫ − L L f ( t ) s i n n ω t d x \begin{align} f(t) &= \frac{a_0} {2} + \sum_{n = 1}^{\infty} \left ( a_n cos n \omega t + b_n sin n \omega t \right) & ,其中L=10 \\ a_0 &= \frac{1}{L}\int_{- L}^{L} f(t)dx \\ a_n &= \frac{1}{L} \int_{- L}^{L} f(t) cos n \omega t dx \\ b_n &= \frac{1}{L} \int_{- L}^{L} f(t) sin n \omega t dx &\end{align} f(t)a0anbn=2a0+n=1∑∞(ancosnωt+bnsinnωt)=L1∫−LLf(t)dx=L1∫−LLf(t)cosnωtdx=L1∫−LLf(t)sinnωtdx,其中L=10
代入图示函数计算:
a 0 = 1 10 [ ∫ 0 10 7 d x + ∫ 0 10 3 d x ] = 1 10 [ 7 ⋅ ( 10 − 0 ) + 3 ⋅ ( 20 − 10 ) ] = 10 \begin{align} a_0 &= \frac{1}{10} \left[ \int_{0}^{10} 7dx + \int_{0}^{10} 3dx \right] \\ & = \frac{1}{10} \left[ 7 \cdot (10-0) + 3 \cdot (20-10) \right] \\ & = 10 \end{align} a0=101[∫0107dx+∫0103dx]=101[7⋅(10−0)+3⋅(20−10)]=10
a n = 1 10 [ ∫ 0 10 7 c o s n ω t d x + ∫ 10 20 3 c o s n ω t d x ] = 1 10 [ 7 n ω s i n n ω t ∣ 0 10 + 3 n ω s i n n ω t ∣ 10 20 ] = 1 n π [ 7 ( s i n n π − s i n 0 ) + 3 ( s i n 2 n π − s i n n π ) ] = 0 \begin{align} a_n & = \frac{1}{10} \left[ \int_{0}^{10} 7 cos n \omega t dx + \int_{10}^{20} 3 cos n \omega t dx \right] \\ & = \frac{1}{10} \left[ \frac{7}{n \omega} sin n \omega t |_{0}^{10} + \frac{3}{n\omega} sin n \omega t |_{10}^{20} \right] \\ & = \frac{1}{n \pi} \left[ 7 ( sin n \pi - sin 0) + 3 (sin 2n \pi - sin n \pi) \right] \\ & = 0 \end{align} an=101[∫0107cosnωtdx+∫10203cosnωtdx]=101[nω7sinnωt∣010+nω3sinnωt∣1020]=nπ1[7(sinnπ−sin0)+3(sin2nπ−sinnπ)]=0
b n = 1 10 [ ∫ 0 10 7 s i n n ω t d x + ∫ 10 20 3 s i n n ω t d x ] = 1 10 [ − 7 n ω c o s n ω t ∣ 0 10 − 3 n ω c o s n ω t ∣ 10 20 ] = − 1 n π [ 7 ( c o s n π − c o s 0 ) + 3 ( c o s 2 n π − c o s n π ) ] = 4 n π [ 1 − c o s n π ] \begin{align} b_n & = \frac{1}{10} \left[ \int_{0}^{10} 7 sin n \omega t dx + \int_{10}^{20} 3 sin n \omega t dx \right] \\ & = \frac{1}{10} \left[ - \frac{7}{n \omega} cos n \omega t |_{0}^{10}- \frac{3}{n\omega} cos n \omega t |_{10}^{20} \right] \\ & = - \frac{1}{n \pi} \left[ 7 ( cos n \pi - cos 0) + 3 (cos 2n \pi - cos n \pi )\right] \\ & = \frac{4}{n \pi} \left[ 1 - cos n \pi \right] \end{align} bn=101[∫0107sinnωtdx+∫10203sinnωtdx]=101[−nω7cosnωt∣010−nω3cosnωt∣1020]=−nπ1[7(cosnπ−cos0)+3(cos2nπ−cosnπ)]=nπ4[1−cosnπ]
当 n n n是奇数时, c o s n π = − 1 cos n \pi = -1 cosnπ=−1,此时 b n = 8 n π b_n = \frac{8}{n \pi} bn=nπ8;
当 n n n是偶数时, c o s n π = 1 cos n \pi = 1 cosnπ=1,此时 b n = 0 b_n = 0 bn=0;
最后,图示函数的傅里叶级数展开为:
F ( t ) = { 5 + ∑ n = 1 ∞ ( 8 n π s i n n π 10 t ) , n = 2 k + 1 , k ∈ z 5 , n = 2 k , k ∈ z \begin{align} F(t) = \left\{\begin{matrix} 5 + \sum_{n=1}^{\infty} (\frac{8}{n \pi} sin \frac{n \pi}{10} t),& n=2k+1,k \in z \\ 5 , & n=2k,k \in z \end{matrix}\right. \end{align} F(t)={5+∑n=1∞(nπ8sin10nπt),5,n=2k+1,k∈zn=2k,k∈z
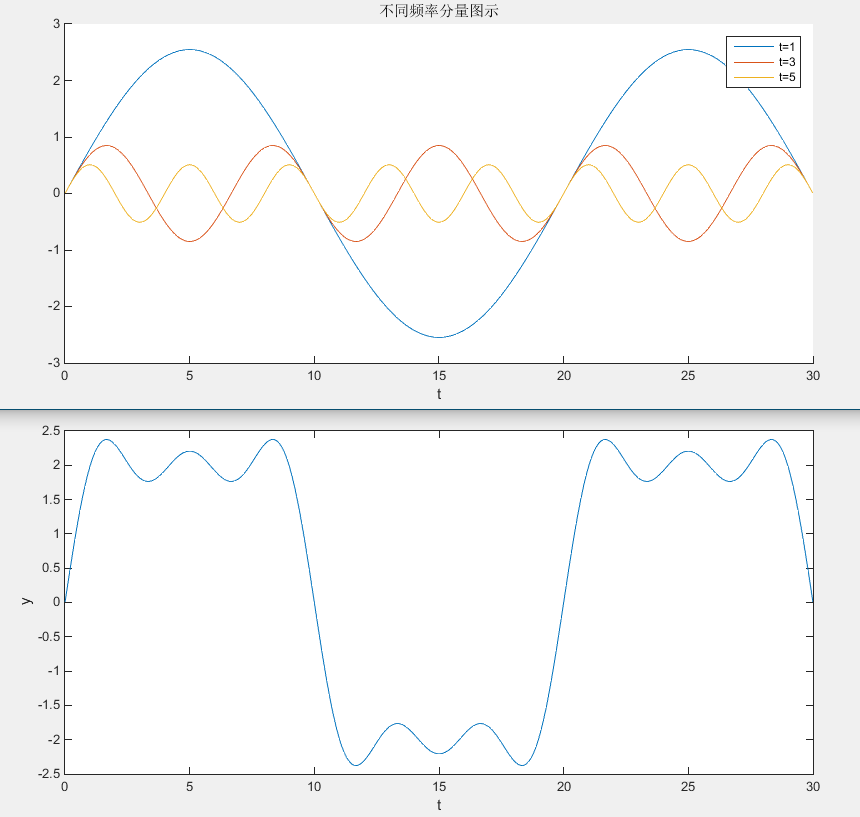
从展开函数中可以发现,当 n n n越大时, 8 n π \frac{8}{n \pi} nπ8越小, n π 10 \frac{n \pi}{10} 10nπ越大即频率越高。现在取 n = 1 , 3 , 5 n=1, 3, 5 n=1,3,5,得到每个频率分量分别为:
n = 1 时为 8 π s i n π 10 t ; n = 3 时为 8 3 π s i n 3 π 10 t ; n = 5 时为 8 5 π s i n 5 π 10 t ; \begin{align} n =1时为 \frac{8}{ \pi} sin \frac{ \pi}{10} t; \\ n = 3 时为 \frac{8}{3 \pi} sin \frac{3 \pi}{10} t; \\ n = 5 时为 \frac{8}{5 \pi} sin \frac{5 \pi}{10} t; \\ \end{align} n=1时为π8sin10πt;n=3时为3π8sin103πt;n=5时为5π8sin105πt;
这三个频率以及它们叠加后的图示如下,可以发现,频率越大,其振幅越小,叠加后的变化大致与给定示意图一致。