目录
正态分布
正态分布的参数
正态分布的第一个参数是均值
正态分布的第二个参数是标准差SD
所有正态分布的共同特征
标准正态分布:正态分布的特例
中心极限定理
理解定义
示例# 1
示例# 2
知道样本均值总是正态分布的实际含义是什么?
正态分布
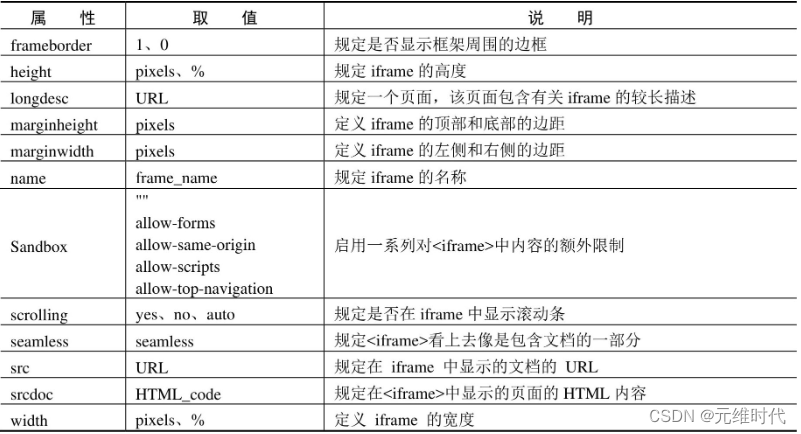
正态分布也被称为高斯分布或钟形曲线(因为它看起来像一个钟),这是统计学中最重要的概率分布,就像我们在大自然中经常看到的那样,它有点神奇。例如,身高、体重、血压、测量误差、智商得分等都服从正态分布。
还有一个跟它相关的,并且非常重要的概念,叫中心极限定理,我们后面会提到。

由上图可得一个正常变量的值是如何分布的。这是一个对称分布,其中大多数观测值聚集在具有最高发生概率的中心峰(均值/平均值)附近,并且当我们在两个方向上都偏离中心峰时,我们看到曲线尾部出现值的可能性越来越小。此图描绘了一个群体的智商水平,可以理解,智商水平非常低或智商水平很高的人很少见,并且大多数人都处于平均智商得分范围内。
正态分布的参数
正态分布总是以平均值为中心,而曲线的宽度则由标准差(SD)决定。

这是两个正态分布,x轴上的高度单位是英寸,y轴上是特定高度对应的人数。
1. 婴儿的平均身高为20英寸(50cm),标准差为0.6英寸(1.5cm)
2. 成年人的平均分布为70英寸(175cm),标准差为4英寸(10cm)
了解正态分布标准差的意义在于,它遵循一个经验法则,即大约95%的测量值落在均值附近的+/- 2倍个标准差之间。
推论:95%的人口落在平均值+/- 2*SD之间
1. 95%的婴儿身高在20 +/- 1.2英寸之间
2. 95%的成年人身高测量值在70 +/- 8英寸之间
正态分布的第一个参数是均值
均值或平均值是正态分布的集中趋势,它决定了曲线峰值的位置。平均值的变化导致曲线沿x轴水平移动。
正态分布的第二个参数是标准差SD
标准差是正态分布变异性的量度,它决定了曲线的宽度。SD值的变化导致曲线变得更窄或更宽,并对曲线的高度产生反比例的影响。
更紧的曲线(较小的宽度)->更高的高度
更宽的曲线(更高的宽度)->更短的高度
现在,你已经了解了正态分布曲线的所有基础知识。让我们继续学习与之相关的其他重要信息。

所有正态分布的共同特征
1. 它们都是对称的
2. 平均值=中位数
3. 根据经验法则,我们可以确定正态分布曲线离均值标准差范围内的数据百分比。
通过一个示例,这一点将变得更加清楚。

让我们来看一个披萨外卖的例子。假设一家披萨餐厅的平均配送时间为30分钟,标准偏差为5分钟。根据经验法则,我们可以确定68%的交付时间在25-35分钟(30 +/- 5)之间,95%在20-40分钟(30 +/- 2*5)之间,99.7%在15-45分钟(30 +/-3*5)之间。
标准正态分布:正态分布的特例
如前所述,正态分布根据参数值(平均值和标准差)有许多不同的形状。标准正态分布是正态分布的一个特例,均值为0,标准差为1。这个分布也称为Z分布。标准正态分布上的值称为标准分数或Z分数。标准分数表示某一特定观测值高于或低于平均值的SD数。
例如,标准得分为1.5表示观察到的结果比平均值高1.5个标准差。另一方面,负分数表示低于平均值的值。平均值的Z分数为0。
中心极限定理

中心极限定理(CLT)指出,如果样本量足够大,则变量均值的采样分布将近似于正态分布,而与该变量在总体中的分布无关。
理解定义
示例# 1

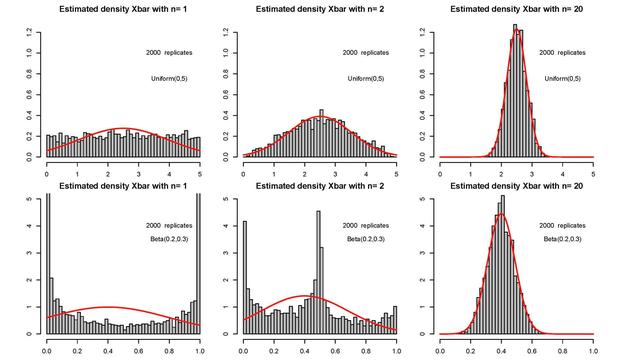
选取一个均匀分布[0,1],它被称为均匀分布,因为在0和1之间选择值的概率相等,因此它的概率密度函数(PDF)是水平的直线。现在,让我们假设我们从这个分布中随机抽取20个样本(绿点)并计算这些样本的均值,我们得到一个值,在这个例子中是0.5,用虚线表示。让我们把这个平均值画在直方图上。由于这个柱状图到目前为止只有一个平均值,它并没有告诉我们任何其他信息(左图)。继续从相同的分布中提取更多的随机样本,计算各自的平均值并将这些平均值绘制在直方图上,我们开始得到一个有趣的结果。
随着我们从均匀分布中抽取越来越多的随机样本,并在直方图上绘制样本均值,我们得到一个正态分布结果如下(见右曲线)。

推论:我们从均匀的数据分布开始,但是从中抽取的样本均值是正态分布。
示例# 2
在第二个例子中,让我们按照与第一个例子相同的步骤,唯一的不同是我们这次要从指数分布中提取样本。

我们将再次随机抽取20个样本,计算样本的均值,并将其绘制在直方图上。计算100这样的样本的均值并将其画在直方图上,这样的分布对我们来说并不陌生。样本均值是正态分布!

推论:我们从指数数据分布开始,但从中抽取样本的均值得到正态分布。
我们从指数数据分布开始,但是从中抽取的样本均值得到正态分布。因此,它在这一点上变得非常直观,中心极限定理意味着什么?
中心极限定理意味着即使数据分布不是正态的,从中抽取的样本均值的分布也是正态的。
知道样本均值总是正态分布的实际含义是什么?
在分析领域,我们每天都会遇到各种各样的数据,而源数据的分布并不总是被我们所知道的,但是,因为我们了解中心极限定理,所以我们甚至不需要关心源数据的分布,因为我们总是可以得到正态分布。
为了使中心极限定理能够起作用,我们必须能够计算出样本的平均值。有一个分布称为柯西分布,没有样本均值,从而中心极限定理论并不适用于它,但除了柯西分布,我没有遇到除中心极限定理以外的任何其他分布。)
下面是了解均值正态分布的实际含义:
1. 我们可以用均值的正态分布来分配置信区间。
2. 我们可以进行T检验(即两个样本均值之间是否存在差异)
3. 我们可以进行方差分析(即3个或更多样本的均值之间是否存在差异)