• Mathematica 常见指令汇编

Mathematica 常见指令

NDSolve 求解结果的保存

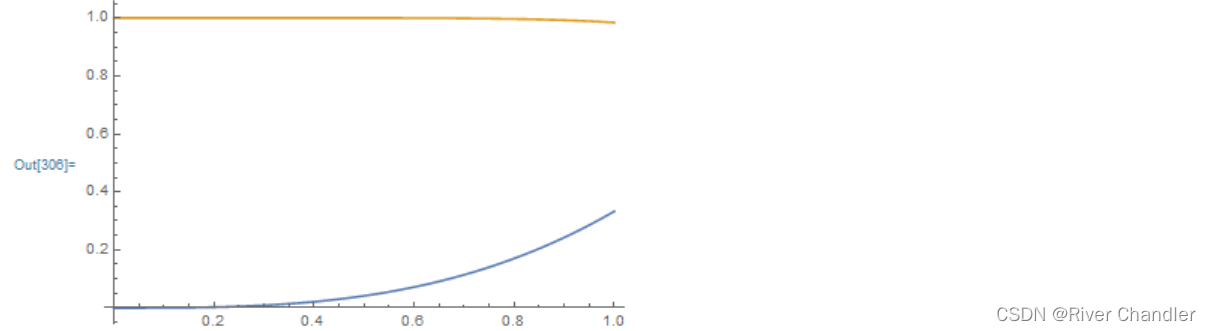
sol = NDSolve[{y'[x] == x^2, y[0] == 0, g'[x] == -y[x]^2, g[0] == 1}, {y, g}, {x, 0, 1}];
numericSoly = sol[[1, 1, 2]];
numericSolg = sol[[1, 2, 2]];
data = Table[{x, numericSoly[x], numericSolg[x]}, {x, 0, 1, 0.01}];
dataset = Dataset[AssociationThread[{"x", "y", "g"}, #] & /@ data];
Export["C:\\Users\\LX\\Desktop\\data.csv", dataset]Plot[{numericSoly[x], numericSolg[x]}, {x, 0, 1}]

 

FindMinimum 求解结果的保存

f[x_, y_] := x^2 + y^2;
constraint = {x + y >= 1, Abs[x - y] >= 0.5};
sol = FindMinimum[{f[x, y], constraint}, {{x, 0}, {y, 0}}]minimizedVariables = sol[[2]];
minimumValue = sol[[1]];data = {{"x", "y", "f(x, y)"}, {minimizedVariables[[1]][[2]], minimizedVariables[[2]][[2]], minimumValue}};
Export["C:\\Users\\LX\\Desktop\\result.xlsx", data]

FindMinimum 不支持在整数规划以外的不等约束与域约束

 

• 要解决这个问题，我们需要借助Matlab 的力量

Matlab 常见指令

odefun

g = @(t, w) t - w;%f = @(x, y) x^2 + y^2 - integral2(@(t, w) g(t, w), x, y, y, x);
f = @(x) x(1)^2 + x(2)^2 - integral2(@(t, w) g(t, w), x(1), x(2), x(1), x(2));nonlcon = @nonlinearConstraint;
A = [-1 -1;1 -1;1 -1];
b = [-1;-0.5;-0.5];

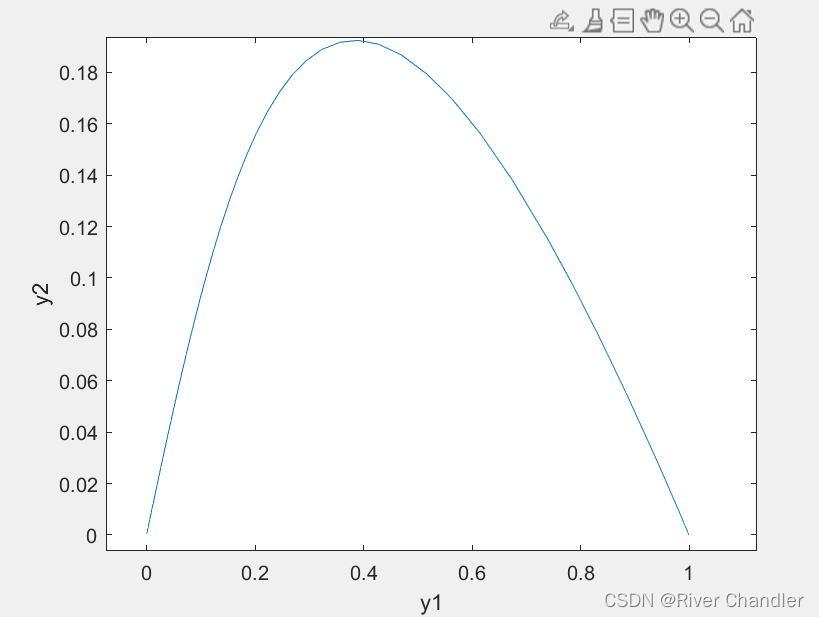
odefun = @(t, y) [-2*y(1) + y(2); y(1) - 2*y(2)];
tspan = [0 100];
y0 = [1; 0];
[t, y] = ode45(odefun, tspan, y0);
%plot(t, y(:, 1), 'r', t, y(:, 2), 'b');
%legend('y_1', 'y_2')
plot(y(:, 1), y(:, 2))
xlabel('y1')
ylabel('y2')

Optimization tools 的 matlab 替代

• 针对FindMinimum 不支持在整数规划以外的不等约束与域约束
• 问题

Untitled.m 

g = @(t, w) t - w;%f = @(x, y) x^2 + y^2 - integral2(@(t, w) g(t, w), x, y, y, x);
f = @(x) x(1)^2 + x(2)^2 - integral2(@(t, w) g(t, w), x(1), x(2), x(1), x(2));nonlcon = @nonlinearConstraint;
A = [-1 -1;1 -1;1 -1];
b = [-1;-0.5;-0.5];

nonlinearConstraint.m 

function [c, ceq] = nonlinearConstraint(x)h = @(p, q) p + 2 * q;%k = @(x) integral2(@(p, q) h(p, q), x(1), x(2), x(1), x(2))-0.25;c = [0.25 - integral2(@(p, q) h(p, q), x(1), x(2), x(1), x(2))];ceq = [0];
end 

Optimizaation Tool 

Optimizaation Tool 微操

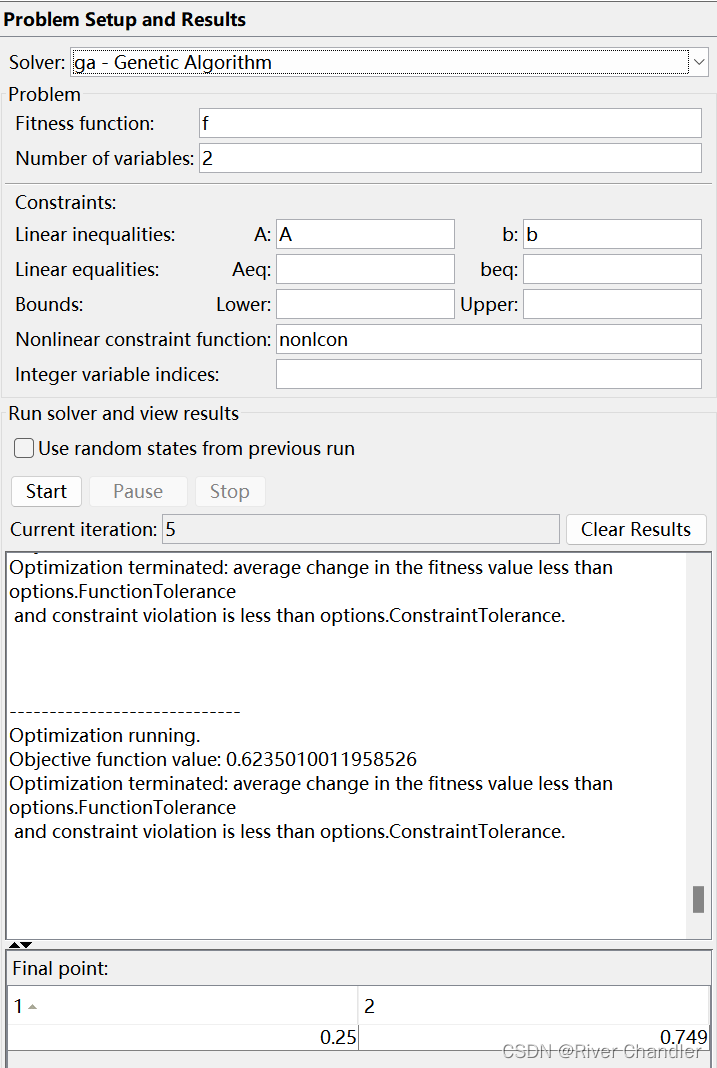
% 定义目标函数
fun = @(x) f(x);% 定义非线性约束函数
nonlcon = @(x) constraints(x);% 定义变量边界
lb = [-10, -10];
ub = [10, 10];% 设置优化选项
options = optimoptions('ga', 'Display', 'iter');% 调用遗传算法进行求解
[x, fval] = ga(fun, 2, [], [], [], [], lb, ub, nonlcon, options);% 输出结果
disp('最优解:');
disp(x);
disp('最小值:');
disp(fval);% 定义目标函数 f(x)
function y = f(x)y = x(1)^2 + x(2)^2;
end% 定义非线性约束函数
function [c, ceq] = constraints(x)c = x(1) - x(2) - 2;g = @(t) t^2 - t + 5;h = @(t) t^3;ceq = g(x(1)) - h(x(2));
end