1 GCN

公式：

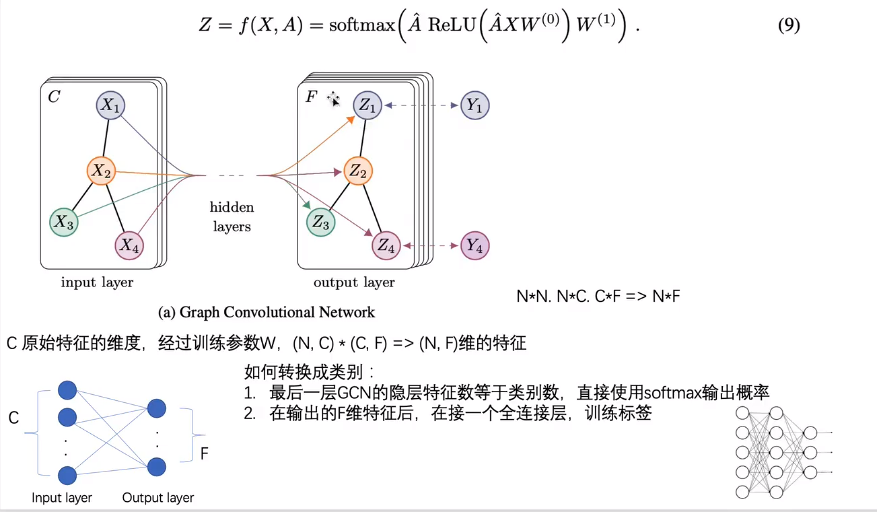
节点的特征从C维(X1)——》F维(Z1)，并 进行softmax操作，得到每一个节点对应的label(Y1)

2 GraphSAGE

实例：

1. 聚合周围邻居信息（领域特征），下图是求平均值
2. 把邻居信息拼接到一起，再经过一个可学习的w参数

2.1 采样：采样固定长度的邻居

节点4是单向的，所以不考虑

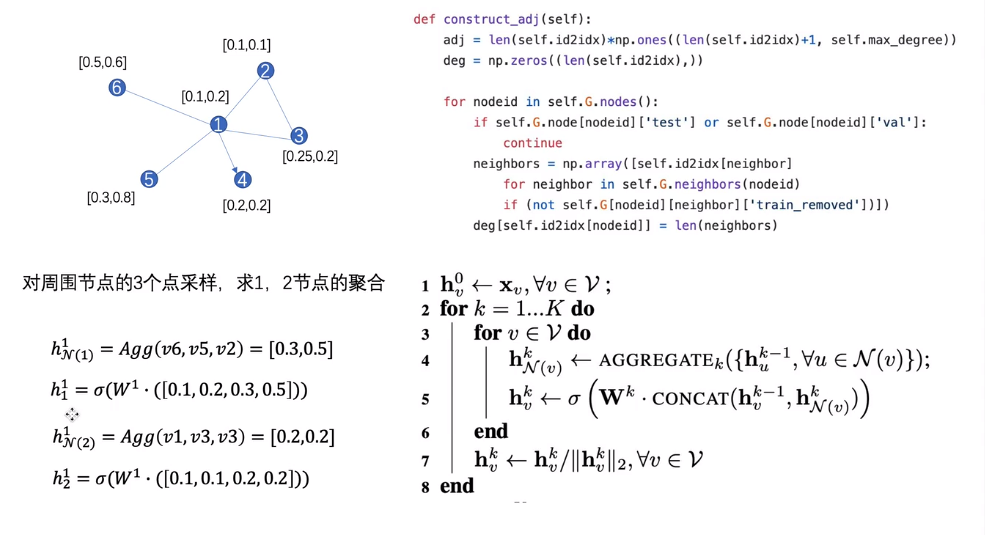
2.2 聚合

要满足以下性质：

1. 聚合函数是对称的
2. 聚合函数的输入和顺序是不变的

2.3 GraphSAGE_minibatch

Minbatch : GraphSAGE采用聚合邻居，和GCN使用全图方式，变成采样。这样在minbatch下，可以不使用全图信息，这使得在大规模图上训练变得可行。把大图转换成小图

例子

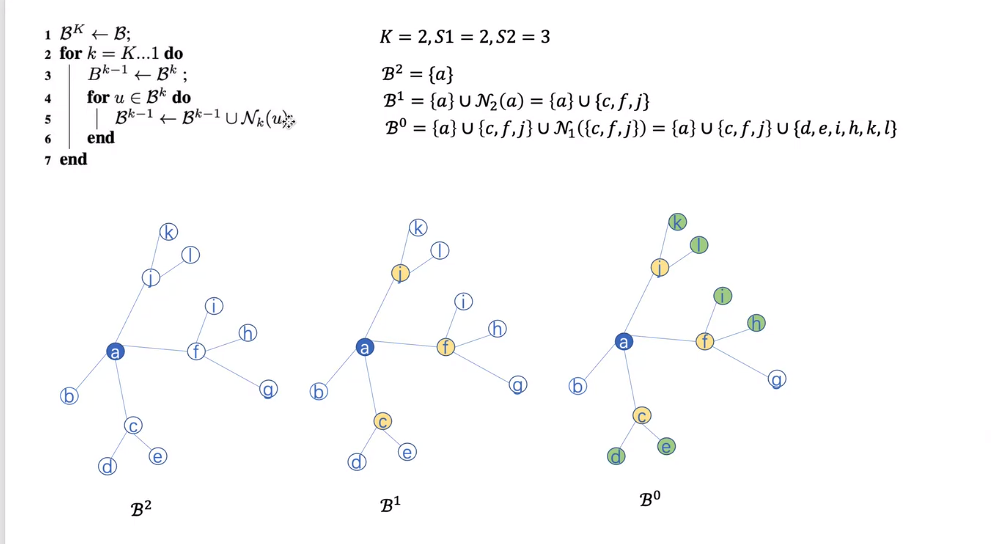
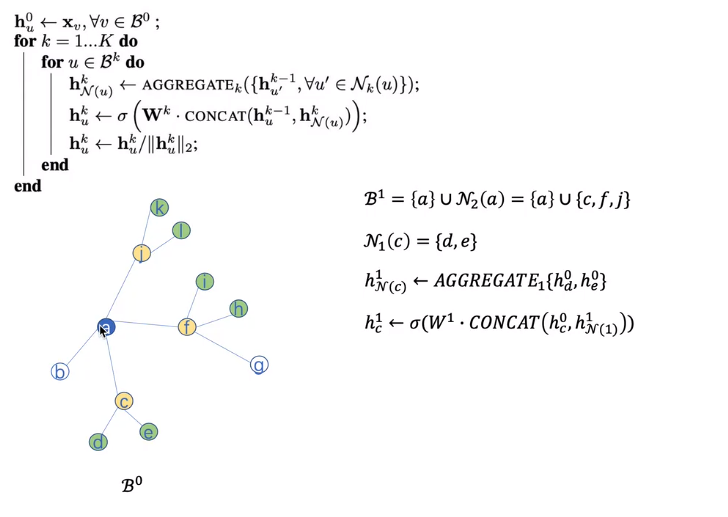
2.4 GraphSAGE_embedding

作者提出的假设：如果这两个节点很近，那么他们的表征应该是相似的，反之，则他们的表征会有所不同

3 GAT

求得节点i和周围节点的attention系数，再通过系数与邻居节点加权求和，那么就求得了该节点聚合周围节点后的特征。

多头注意力机制

三个节点表示了三类特征

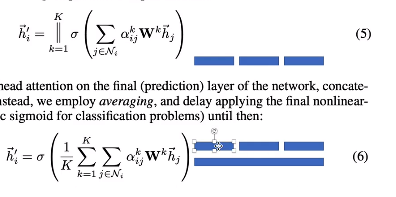
4. 图网络的分类

4.1 递归图神经网络 RGNN

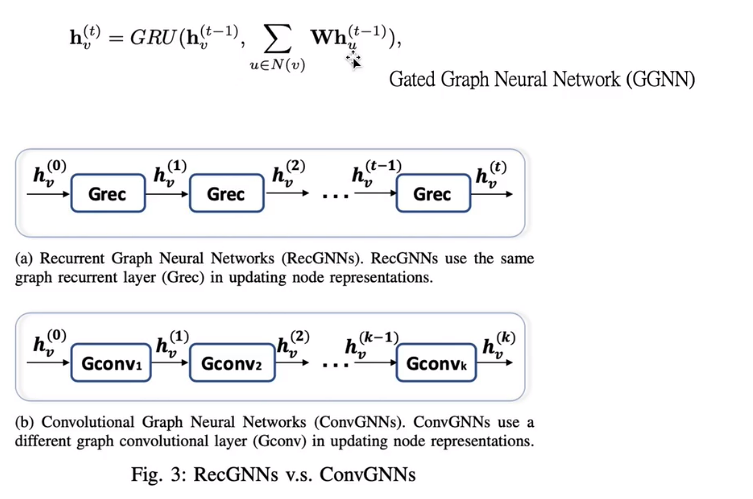
递归和卷积都是学习特征，很明显，卷积图神经网络的卷积层参数可以是不一致的的

4.2 图卷积神经网络GCN

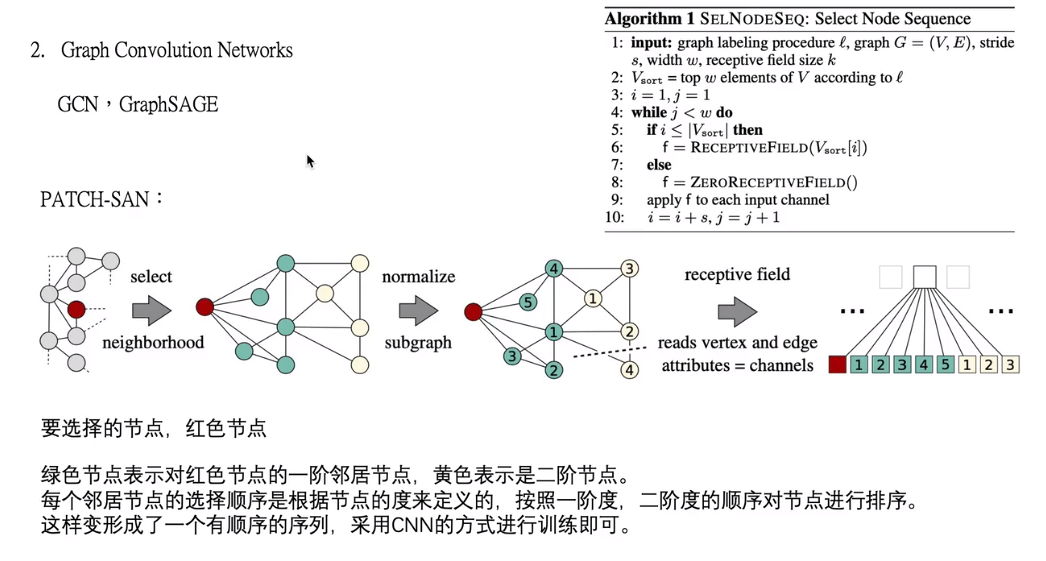
得到节点有序序列

4.3 图注意力网络 GAT

4.4 图自动编码 GAE

GAE：encoder用GCN替换，得出的特征矩阵Z，decoder替换成Z的转置，通过转置生成的图与原图比较得出最小化结构性误差，通过最小损失函数可以得出GCN的参数

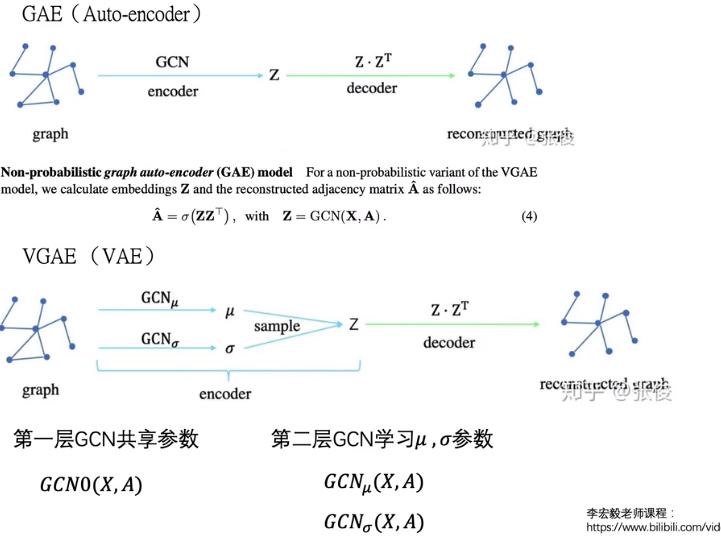
VAE课程，李宏毅老师课程∶
https://www.bilibili.com/video/BV1tZ4y1L7gu?from=search&seid=15594710630639930905

4.5 图时空网络 GSTN

同时考虑图的空间性和时间维度·比如在交通邻域中﹐速度传感器会随时间变化的时间维度﹐不同的传感器之间也会形成连接的空间维度的边。
当前的许多方法都应用GCN来捕获图的依赖性，使用一些RNN或CNN对时间依赖性建模。

4.6 图生成网络 GGN

通过RNN或者GAN的方式生成网络。图生成网络的
一个有前途的应用领域是化合物合成。在化学图中﹐原子被视为节点﹐化学键被视为边·任务是发现具有某些化学和物理性质的新的可合成分子。

4.7 图强化学些 GRL

通过RNN或者GAN的方式生成网络。图生成网络的
一个有前途的应用领域是化合物合成。在化学图中﹐原子被视为节点﹐化学键被视为边·任务是发现具有某些化学和物理性质的新的可合成分子。

4.8 图对抗方法GAM

GAN的思想﹐生成器生成样本﹐分类器去判别样本。

4.9 更通用的框架

1. MPNN∶图神经网络和图卷积/ Message Passing Neural Networks
2. NLNN︰统一Attention/ Non-local Neural Networks
3. GN︰统一以上/ Graph Networks

4.9.1 消息传递网络 MPNN

Mt：聚合周围邻居信息

Ut：更新节点在下一层的特征表示

前面这两部分就跟GraphSAGE相似；最后，组合在一起就成了图的表示y hat。

4.9.2 非局部神经网络 NLNN

f（）求的就是节点i和相邻节点的attention系数，再求g（）得出的该节点的特征，再归一化就是下一层的特征表示yi‘。

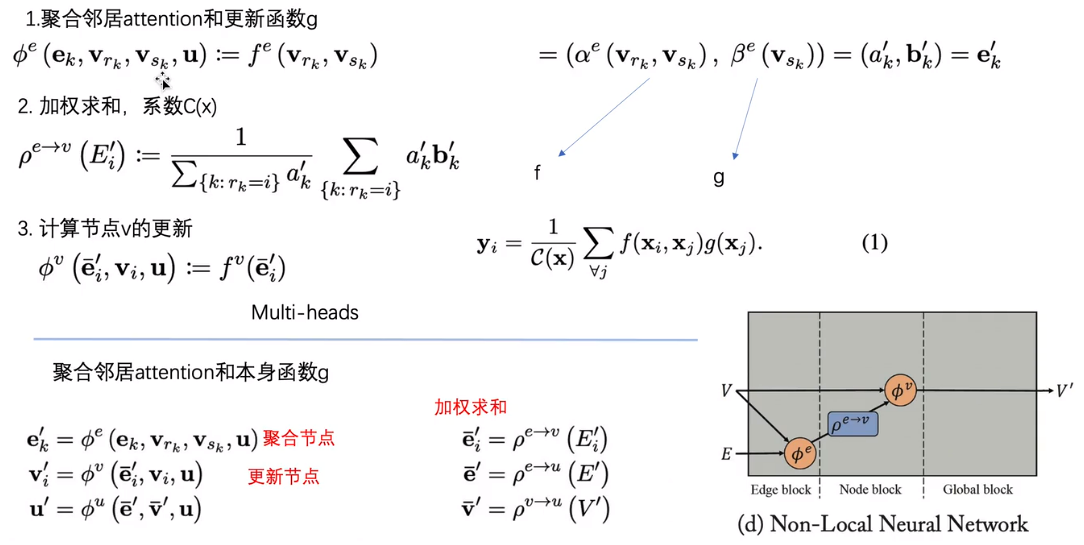
4.9.3 图神经网络 GN

一个GN块包含三个更新函数函数φ和三个聚合函数ρ，各符号意义如下图所示：

一个例子：Vsk：sender node；Vrk：receiver node；

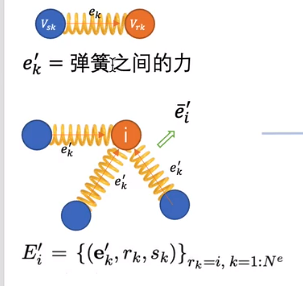
计算流程如下：

整个算法的流程：

MPNN应用于GN

NLNN应用于GN

4.10 其他图

1. 异构图

不同节点构成的图

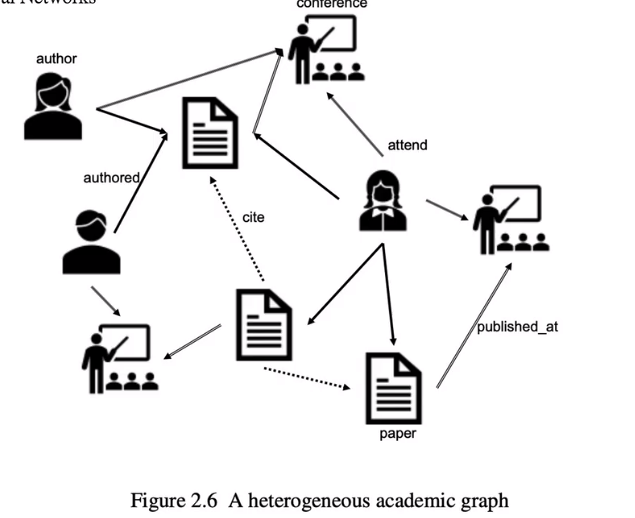
2. 二部图

将图中节点分为两部分，每一边不跟自己相连

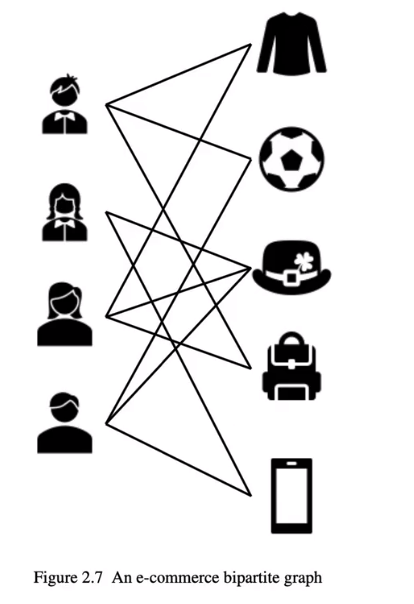
3. 多维图

多种关系所组成的图

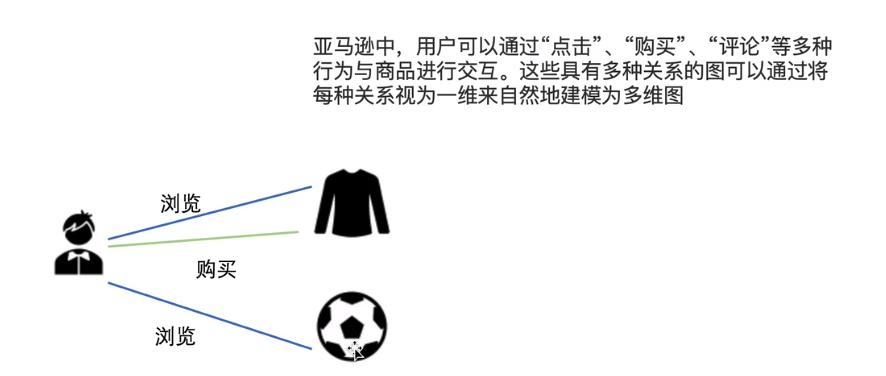
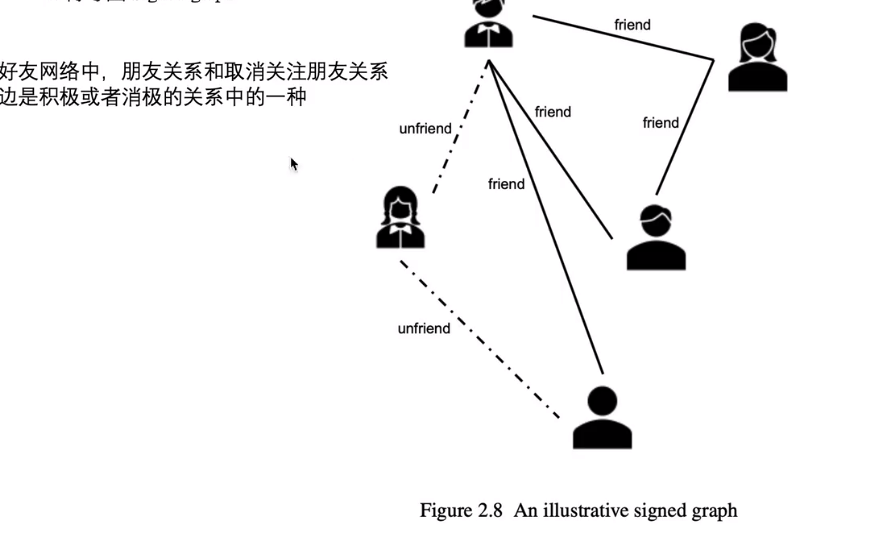
4. 符号图

图之间的连接有正反符号

5. 超图

一条边包含两个以上的节点。每个边所包含的顶点个数都是相同且为k个的，就可以被称为k阶超图，常见的图就是2阶超图。

6. 动态图

上面提到的图是静态的，观察时节点之间的连接是固定的。但是，在许多实际应用中，随着新节点被添加到图中，图在不断发展，并且新边也在不断出现。例如，在诸如Facebook的在线社交网络中，用户可以不断与他人建立友谊，新用户也可以随时加入Facebook。这些类型的演化图可以表示为动态图，其中每个节点或边都与时间戳关联。