在蛋白质世界,“结构决定功能”是一条基本原则。因此,很多人可能认为,一个蛋白质就应该有一个唯一确定的结构,使得它能够去执行确定的生物学功能。其实,在真实的世界中,蛋白质大多都是处于一种不断起伏的动力学的状态。特别是,有一类蛋白质,它们的结构的起伏大到可以认为它们是处于完全不同的两种状态。

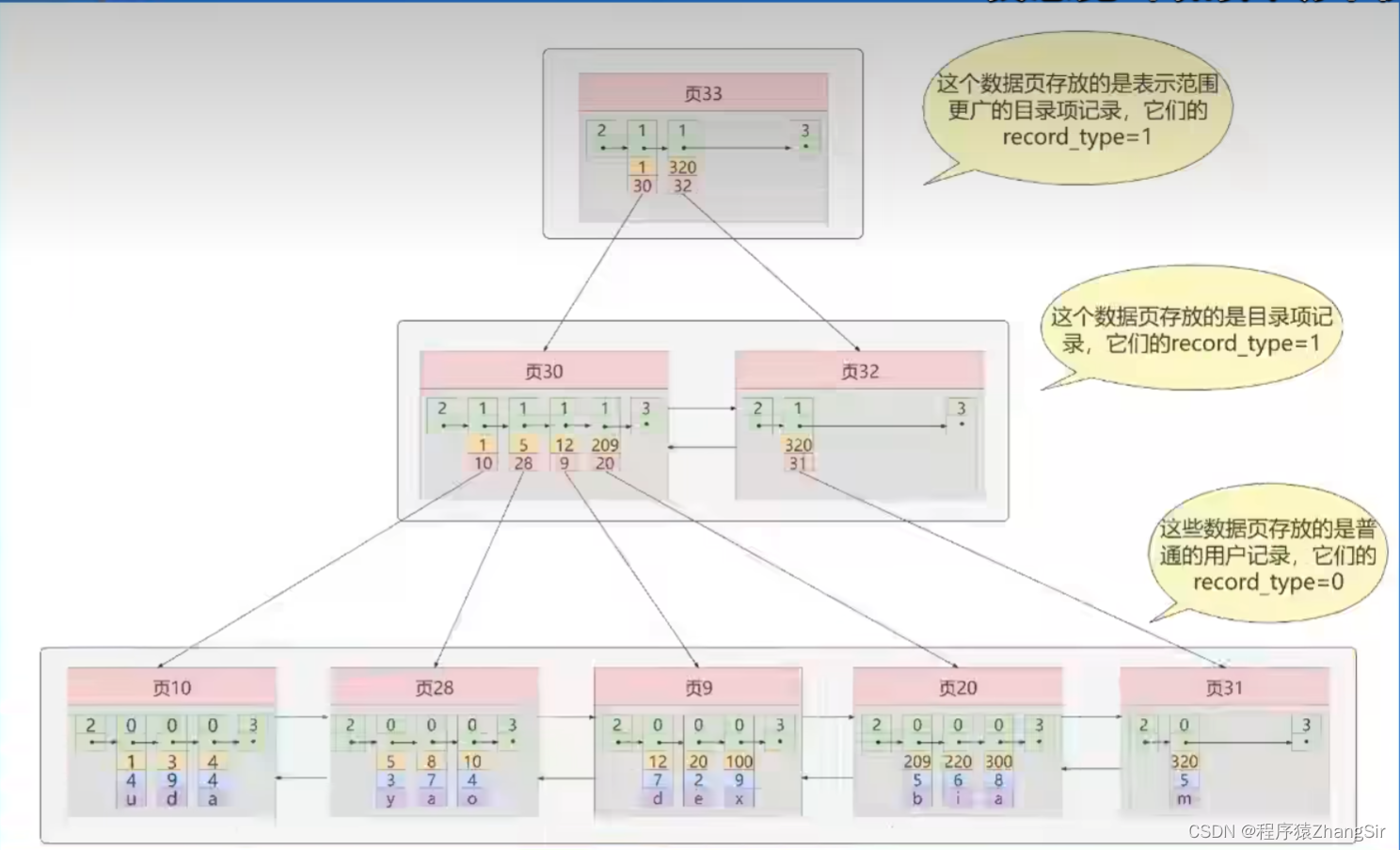
具有两种不同构型的蛋白质在与药物靶点结合之前和之后会形成不同的结构(示意图)
近年来,随着AI技术的发展,计算机蛋白质设计进展也很快。但是绝大多数计算机蛋白质设计都是设计具有某种特定结构执行某种特定功能的蛋白质。如何设计出具有多种构型的蛋白质,是一种全新的挑战。这对于科学家完全理解蛋白质构型的起伏,功能对构型的动态依赖,其中至关重要的作用。
2023年8月17日,蛋白质设计领域先驱、华盛顿大学 David Baker 教授在国际著名杂志《Sicence》期刊发表了题为:“刺激响应二态铰链蛋白的设计” (Design of stimulus-responsive two-state hinge proteins)的研究论文,来试图解决双构型蛋白的设计问题。
该研究通过人工智能(AI)辅助设计(ProteinMPNN),开发出一种铰链样蛋白质。这种铰链蛋白同时具有两种明确的构象,在与目标蛋白结合时显示出稳定的构象变化,因此可以根据这种特异性定制出“蛋白质开关”。这项工作为产生响应生物刺激的蛋白质开关提供了研究基础,为蛋白设计领域带来全新变革!

在自然界中,许多天然蛋白质可以在两种构象之间转换以响应环境刺激,例如目标分子的结合、翻译后修饰或pH的变化。这个过程在结构上类似于晶体管控制计算设备中的电子信息流,只不过蛋白质传递的是生化信息。
然而,天然蛋白质都是经过漫长的进化才衍化得来,人工设计的蛋白往往很难做到在两种折叠状态之间进行这样的构象转换。因为人工蛋白质设计通常旨在优化一个单一的、非常稳定的构象,使其拥有折叠能量景观的全局最小值。
因此,如何设计出同时具有两种不同构象且结构完整的人工蛋白质是蛋白质设计领域的一个重大挑战。其中,最关键的一个要求是,所设计的蛋白质需要同时具有两个不同最小值的能量景观,就像一座山峰之中同时有两个山坳,一片沙漠之中同时有两个绿洲。
在这项最新研究中,David Baker 团队描述了一种铰链蛋白的设计概念,这种蛋白具有两个明确定义和结构的构象状态:在没有配体的情况下表现为X设计状态,而在配体存在的情况下通过构象变化转换为Y设计状态。

可以在不同构象之间转换的蛋白质的设计策略
Baker实验室通过X射线晶体学、电子显微镜、双电子-电子共振光谱等技术对设计的铰链蛋白的蛋白质结构、结合动力学和构象平衡进行了全面表征。研究结果表明,尽管存在显著的结构差异,但这两种构象状态的设计具有原子水平的精度,并且构象平衡和结合平衡是紧密耦合的。

多态铰链蛋白的实验验证:两种设计状态的晶体结构与设计模型高度一致
因此,这种铰链蛋白可以广泛适用于蛋白质开关的设计,就像是电子电路中的晶体管一样,研究人员可以将蛋白质开关与外部输出和输入耦合,其状态转换通过与天然蛋白(例如胰高血糖素、神经肽、分泌素)结合而不是人工设计肽。

所设计的铰链蛋白构象变化的定量分析
基于这种设计的铰链蛋白可以用于创建生物传感设备,并将它们合并到更大的蛋白质系统中,以解决各种突出的设计挑战:铰链蛋白可以作为一种模块,在其内部安装特定的酶活位点,从而实现两种明确构象的切换——当底物结合时有利于一种状态,当产物释放时有利于另一种状态。
这对于之前的LOCKR开关而言是不可能的,因为LOCKR开关只有一个明确的构象,另一个状态往往是无序的。缺乏定义的第二状态使得它不适合于构建蛋白质开关或基于离散状态的计算系统中的机械耦合。
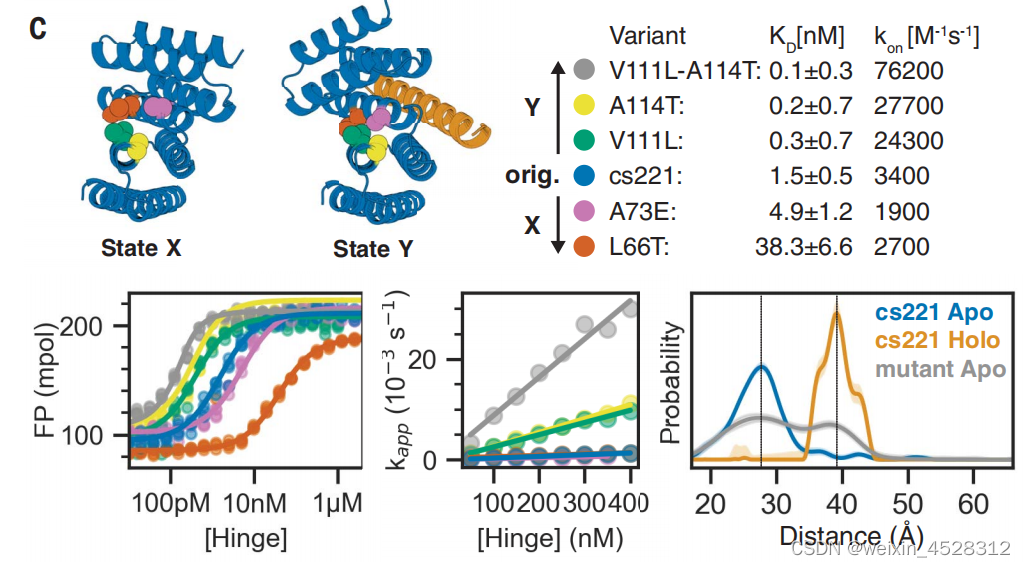
控制构象预平衡会影响肽的结合
总的来说,这项新研究开发出了同时具有两种明确状态的铰链蛋白,可以应用于“蛋白质开关”的设计。这种双态开关的研究能使蛋白质设计超越静态结构,转向更复杂的多态组装和生物传感器设计,为蛋白设计提供了更广阔的可能性。
Baker教授团队所在的华盛顿大学蛋白设计研究所首席战略及运营官Lance Stewart博士也表示,自从10年前与蛋白设计领域先驱David Baker教授相识后,人工智能在预测蛋白结构、设计蛋白药物等方面取得了很大进步。在人工智能的协助下,未来谈及不可成药性,不仅是指开发针对不可成药的药物,还包括开发筛选这些药物所用的工具。他说:“现在的新技术让我们有能力去挑战任何类型的靶点,这是当下产业的幸运。”
“我们相信这些铰链蛋白就好像电子产品中的晶体管,” 《Science》论文的共同第一作者,Baker实验室的Phil Leung博士说,“就像晶体管可以对电信号做出反应,这些蛋白可以在分子水平改变形状并且调控生物学相互作用。” 晶体管的出现给电子产品带来了革命性的变化,为数字时代的来临铺平了道路。研究人员相信设计能够在不同构象中变换的蛋白也将给生物科技带来革命性的变化,让全新生物材料、生物感受器以及智能药物递送系统成为可能。
参考文献:
https://www.science.org/doi/full/10.1126/science.adg7731