✨Blog:🥰不会敲代码的小张:)🥰
🉑推荐专栏:C语言🤪、Cpp😶🌫️、数据结构初阶💀
💽座右铭:“記住,每一天都是一個新的開始😁😁😁”
💀本章内容:《树和二叉树》的介绍✨
1.树的概念及结构
树是一种非线性的数据结构,它是由n(n>=0)个有限结点组成一个具有层次关系的集合。把它叫做树是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。
- 有一个特殊的结点,称为根结点,根节点没有前驱结点
- 除根节点外,其余结点被分成M(M>0)个互不相交的集合T1、T2、……、Tm,其中每一个集合Ti(1<= i <= m)又是一棵结构与树类似的子树。每棵子树的根结点有且只有一个前驱,可以有0个或多个后继
- 因此,树是递归定义的
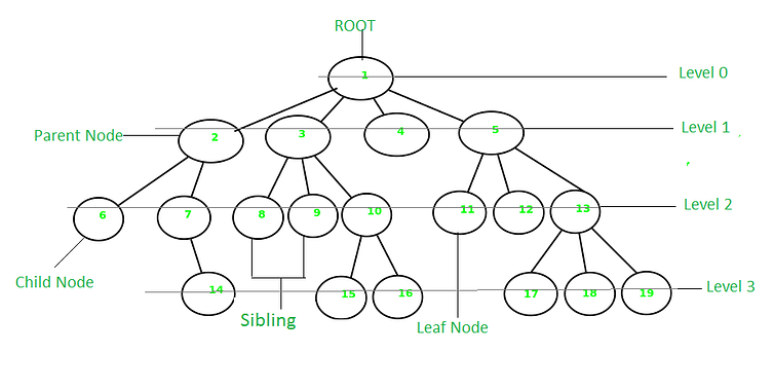
树形结构中,子树之间不能有交集,否则就不是树形结构
目录
- 1.树的概念及结构
- 树的表示
- 树在实际中的运用
- 2.二叉树概念及结构
- 满二叉树和完全二叉树
- 二叉树的存储结构
- 二叉树顺序表存储
- 3.堆的概念
- 用顺序存储完成堆的实现
- 创捷堆需要的结构
- 初始化
- 销毁堆
- 交换两个数
- 向上调整
- 插入
- 向下调整
- 删除
- 返回堆顶
- 判空
- 堆的大小
树的表示
树结构相对线性表就比较复杂了,要存储表示起来就比较麻烦了,既然保存值域,也要保存结点和结点之间的关系,实际中树有很多种表示方式如:双亲表示法,孩子表示法、孩子双亲表示法以及孩子兄弟表示法等。我们这里就简单的了解其中最常用的孩子兄弟表示法。
typedef int DataType;
struct Node
{struct Node* _firstChild1; // 第一个孩子结点struct Node* _pNextSibling; // 指向其下一个兄弟结点DataType _data; // 结点中的数据域
};
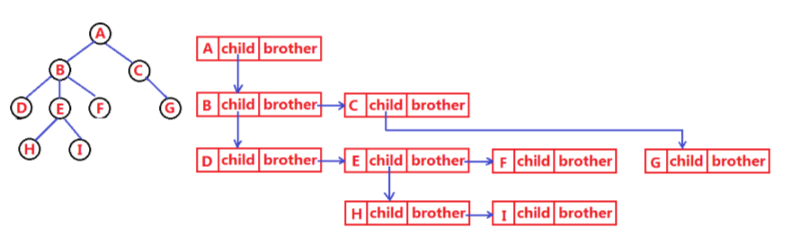
树在实际中的运用
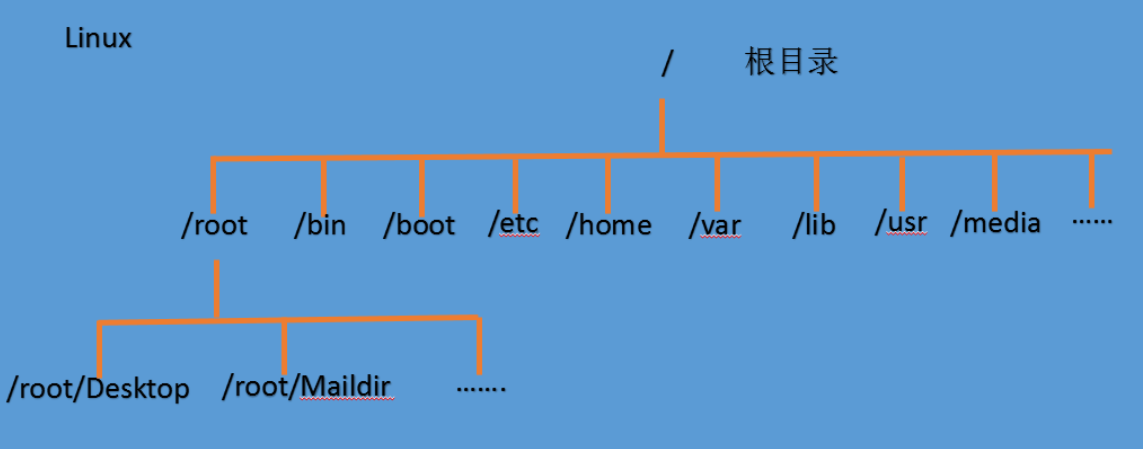
下图可以看得出Linux使用的就是树形结构,父亲节点可以有n个孩子
2.二叉树概念及结构
一棵二叉树是结点的一个有限集合,该集合:
1.或者为空
2.由一个根节点加上两棵别称为左子树和右子树的二叉树组成
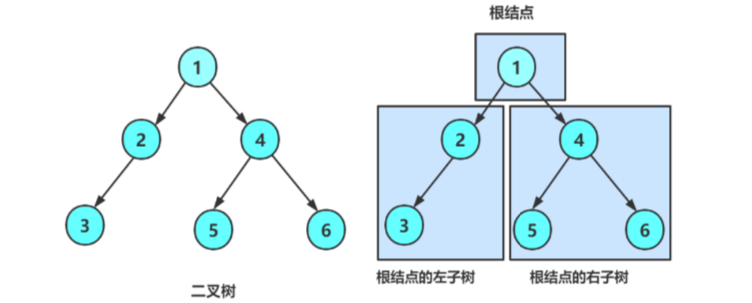
从上图可以看出:
1.二叉树不存在度大于2的结点
2.二叉树的子树有左右之分,次序不能颠倒,因此二叉树是有序树
注意:对于任意的二叉树都是由以下几种情况复合而成的:
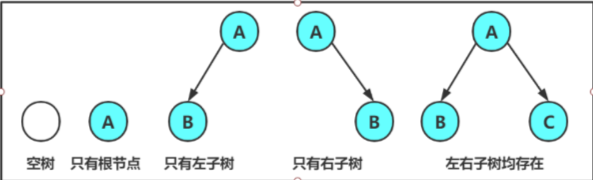
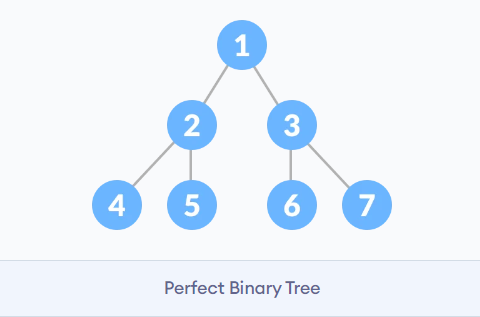
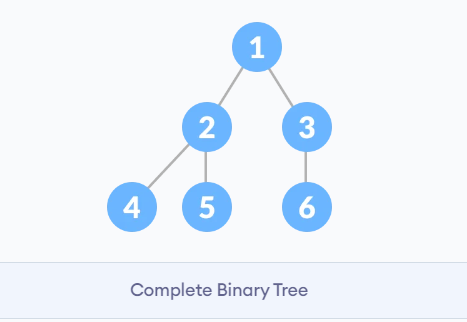
满二叉树和完全二叉树
- 满二叉树:一个二叉树,如果每一个层的结点数都达到最大值,则这个二叉树就是满二叉树。也就是说,如果一个二叉树的层数为K,且结点总数是 ,则它就是满二叉树。
- 完全二叉树:完全二叉树是效率很高的数据结构,完全二叉树是由满二叉树而引出来的。对于深度为K的,有n个结点的二叉树,当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。 要注意的是满二叉树是一种特殊的完全二叉树。
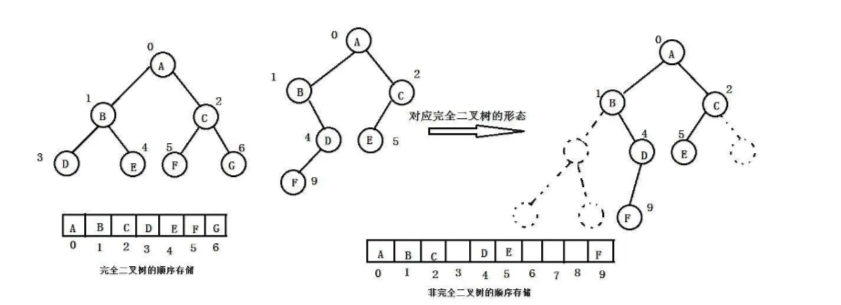
二叉树的存储结构
二叉树一般可以使用两种结构存储,一种顺序结构,一种链式结构。
二叉树顺序表存储
顺序结构存储就是使用数组来存储,一般使用数组只适合表示完全二叉树,因为不是完全二叉树会有空间的浪费。而现实中使用中只有堆才会使用数组来存储,关于堆我们后面的章节会专门讲解。二叉树顺序存储在物理上是一个数组,在逻辑上是一颗二叉树。
顺序表存储二叉树,只适用于完全二叉树否则会有空间上的浪费
3.堆的概念
如果有一个关键码的集合,把它的所有元素按完全二叉树的顺序存储方式存储,在一个一维数组中,将根节点最大的堆叫做最大堆或大根堆,根节点最小的堆叫做最小堆或小根堆。
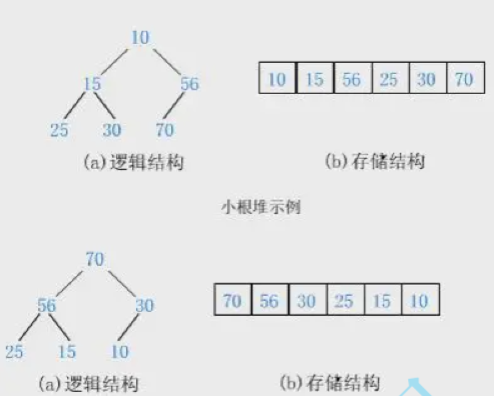
用顺序存储完成堆的实现
一个数组,我们可以看作一个二叉树,但还不是堆,所以使用向上/下调整成一个堆。
- 建堆
升序:建大堆
降序:建小堆 - 利用堆删除思想来进行排序
建堆和堆删除中都用到了向下调整,因此掌握了向下调整,就可以完成堆排序。
表示二叉树的值在数组位置中父子的下标关系
parent = (child-1)/2
leftchild = parent * 2 +1
rightchild = parent * 2 +2
创捷堆需要的结构
typedef int HpDatatype;
typedef struct Heap
{HpDatatype* data;//元素int size;//长度int capcity;//容量
}Heap;
初始化
//初始化
void HeapInit(Heap* php)
{assert(php);php->data = (HpDatatype*)malloc(sizeof(HpDatatype) * 4);if (php->data == NULL){perror("malloc fail");return;}php->size = 0;php->capcity = 4;}
销毁堆
//销毁堆
void HeapDestroy(Heap* php)
{assert(php);free(php->data);php->data = NULL;php->size = 0;php->capcity = 0;}
交换两个数
//交换两个数
void Swap(HpDatatype* p1, HpDatatype* p2)
{HpDatatype tmp = *p1;*p1 = *p2;*p2 = tmp;
}
向上调整
时间复杂度:N*logN
//向上调整
void AdjustUp(HpDatatype* a, int child)
{int parent = (child - 1) / 2;while (child > 0){if (a[child] > a[parent]){Swap(&a[child], &a[parent]);child = parent;parent = (child - 1) / 2;}else{break;}}
}
插入
//插入
void HeapPush(Heap* php, HpDatatype x)
{assert(php);if (php->capcity == php->size){HpDatatype* tmp = (HpDatatype*)realloc(php->data, sizeof(HpDatatype) * php->capcity * 2);if (tmp == NULL){perror("malloc fail");return;}php->data = tmp;php->capcity *= 2;}php->data[php->size] = x;php->size++;AdjustUp(php->data, php->size-1);
}
向下调整
时间复杂度:O(N)
//向下调整
void AdjustDown(HpDatatype* a, int n, int parent)
{int child = parent * 2 + 1;if (child+1 < n && a[child] < a[child + 1]){child++;}while (child < n){if (a[parent] < a[child]){Swap(&a[parent], &a[child]);parent = child;child = parent * 2 + 1;}else{break;}}
}
删除
//删除
void HeapPop(Heap* php)
{assert(php);//assert(!HeapEmpty(php->data));Swap(&php->data[0], &php->data[php->size - 1]);php->size--;AdjustDown(php->data, php->size, 0);
}
返回堆顶
//返回堆顶
HpDatatype HeapTop(Heap* php)
{assert(php);return php->data[0];
}
判空
//判空
bool HeapEmpty(Heap* php)
{assert(php);return php->size == 0;
}
堆的大小
//堆的大小
int HeapSize(Heap* php)
{return php->size;
}