1 P=NP？

P类问题(Polynomial)指在多项式时间内能求解的问题；NP类问题(Non-Deterministic Polynomial)指在多项式时间内能验证一个解的问题。

问题的归约(reduction)指将一个问题的求解等效为另一个问题的求解，其中这种等效具有提升普遍性、加大复杂度的趋势，且问题归约可传递。举例而言，可以将求解一元一次方程归约为求解一元二次方程。

若任意一个NP类问题都能在多项式时间内归约到某个NP问题，则该问题被称为NP完全问题(NP-Complete)；若无法归约到某个NP问题，则该问题被称为NP难问题(NP-Hard)。

P类问题本身是NP的，因为能在多项式时间内求解必然能在多项式时间内验证解。但反之，NP问题是否是P问题的论断称为“P=NP?”，该论断被列为千禧七大难题之首，暂未被证明或证伪。

2 时间复杂度

一般地，算法中基本操作重复执行的次数是问题规模$n$的某个函数$f(n)$。在计算机科学中用时间复杂度(Time Complexity)定性描述一个算法的运行时耗——体现在问题规模$n$变化$c$倍后算法的执行效率，而非针对一个特定的$n$，记为

$$T\left(n\right)=O\left(f\left(n\right)\right)$$

其中$O\left(\cdot \right)$是复杂度度量函数，不包括输入的低阶项和首项系数(非常数项)。必须指出，使用$O\left(\cdot \right)$属于渐进时间复杂度——输入值大小趋近无穷时的情况，否则不能忽略其他低阶项的影响。常见的时间复杂度如下

2.1 常数阶复杂度

常数阶复杂度记为$O(a)$

示例：

// 计算 1 + 2 + 3 + ... + n 的值
int sum(int n)
{return (1 + n) * n / 2;
}

解释：对任意问题规模 ，算法均只执行一次，故认为算法时间复杂度为$O(1)$

2.2 对数阶复杂度

常数阶复杂度记为$O\left(\log n\right)$

示例：

/** 二分查找*    A[] : 待查找的数组(已排序)*      n : 数组长度* target : 查找的目标值*/
int binarySearch(int A[], int n, int target) {int lt = 0, rt = n;while(lt < rt){int mid = lt + (rt - lt)/2;if(A[mid] == target) return mid;else if(A[mid] > target) rt = mid;else lt = mid + 1;}return -1; // 查找不到
}

解释：二分查找算法每次迭代排除一半元素，因此第$m$次迭代后剩余待查找元素个数为$n/2^m$，最坏情况下排除到只剩最后一个值后得到结果——结果为该值或查找不到，即令$n/2^m=1$，则$f\left(n\right)=m={\log }_{2}n$，故认为算法时间复杂度为$O\left(\log n\right)$

2.3 线性阶复杂度

示例：

// 计算 1 + 2 + 3 + ... + n 的值
int sum(int n)
{int sum = 0;for(int i = 1; i <= n; i++) {sum += i;}return sum
}

解释：对任意问题规模$n$，算法均执行$n$次，故认为算法时间复杂度为$O(n)$

2.4 平方阶复杂度

示例：

/** 冒泡排序* arr[] : 待排序数组*     n : 数组长度*/
void bubbleSort(int[] arr, int n) {if(n == 0 || n == 1) return;for(int i = 0; i < n - 1; ++i) {for(int j = 0; j < n - i - 1; ++j) {if(a[j] > a[j+1]) swap(a[j], a[j+1]);}}
}

解释：冒泡排序算法共$n-1$次迭代，每次迭代循环比较$n-i-1$次，故总迭代次数为$\left(n-1\right)+\left(n-2\right)+\cdots +1=n\left(n-1\right)/2$，故认为算法时间复杂度为$O\left(n^2\right)$

2.5 指数阶复杂度

示例：

// 计算斐波那契数列
int fibonacci(int n)
{if (n<=0) return 0;if (n==1) return 1;return fb(n - 1) + fb(n - 2);
}

解释：斐波那契算法本质上是二阶常系数差分方程$f\left(n\right)=f\left(n-1\right)+f\left(n-2\right)$，其特征根为$x_{1,2}=\frac{1\pm \sqrt{5}}{2}$，则该差分方程通解为$f\left(n\right)=c_1{\left(\frac{1+\sqrt{5}}{2}\right)}^n+c_2{\left(\frac{1-\sqrt{5}}{2}\right)}^n$，代入初始条件$f\left(0\right)=0$、$f\left(1\right)=1$解得$c_1$、$c_2$后即得

$$f\left(n\right)=\frac{1}{\sqrt{5}}\left[{\left(\frac{1+\sqrt{5}}{2}\right)}^n-{\left(\frac{1-\sqrt{5}}{2}\right)}^n\right]$$

故认为算法时间复杂度为$O\left(a^n\right)$

2.6 总结

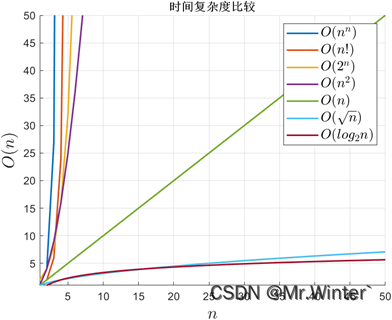
特别地，当$n$处于复杂度底数位置时称为多项式时间复杂度，例如常数阶、对数阶、线性阶等；当$n$处于复杂度指数位置时称为超多项式时间复杂度，例如指数阶、阶乘阶等。一般地，计算机只能处理多项式时间复杂度算法，而无法忍受超多项式时间算法中问题规模的些许增长带来的爆炸式耗时，因此将多项式时间视为算法在时间复杂度层面是否有效的分水岭，如图所示。

3 空间复杂度

在计算机科学中用空间复杂度(Space Complexity)定性描述一个算法的内存占用——体现在问题规模$n$变化$c$倍后算法临时占用内存的增长状况，而非针对一个特定的$n$，记为

$$S\left(n\right)=O\left(f\left(n\right)\right)$$

算法空间复杂度分析与时间复杂度类似，区别在于其关注的不是基础操作的重复次数，而是算法运行时堆栈中的内存消耗，在递归算法中尤为明显。一般地，算法复杂性分析优先考察时间复杂度，而假设空间不受限；对空间复杂度的考察主要集中在嵌入式领域。

下面是归并排序的实例。

/** 归并排序* a[] : 待排序数组*  lt : 排序左索引*  rt : 排序右索引* p[] : 临时数组，存储排序元素*/
void merge(int a[], int lt, int rt, int p[]){int mid = (rt - lt)/2 + lt;int i = lt, j = mid + 1;int k = 0;// 合并while(i <= mid && j <= rt){ if(a[i] <= a[j])  p[k++] = a[i++];else              p[k++] = a[j++];}// 合并剩余while(i <= mid)         p[k++] = a[i++];while(j <= rt)          p[k++] = a[j++];// 重新赋值回去for(i = 0; i < k; ++i)  a[lt+i] = p[i];
}// 划分
void mergeSort(int a[], int lt, int rt, int p[]){if(lt < rt){int mid = (rt - lt)/2 + lt;mergeSort(a, lt, mid, p);   // 递归排序 lt ~ midmergeSort(a, mid+1, rt, p); // 递归排序 mid+1 ~ rtmerge(a, lt, rt, p);        // 合并 lt ~ rt}
}

设问题规模为$n$，即待排序元素为$n$个，则递归调用时最坏情况下会产生${\log }_{2}n$层递归树。若临时数组在全局作用域中开辟，则递归过程中不再开辟新的内存空间，空间复杂度为$O(n)$；若临时数组在栈中申请，则每层递归都要开辟一次长度为$n$的临时空间，空间复杂度为$O\left(n{\log }_{2}n\right)$

---

🔥 更多精彩专栏：

• 《ROS从入门到精通》
• 《Pytorch深度学习实战》
• 《机器学习强基计划》
• 《运动规划实战精讲》
• …

👇源码获取 · 技术交流 · 抱团学习 · 咨询分享 请联系👇