1 530. 二叉搜索树的最小绝对差

530. 二叉搜索树的最小绝对差

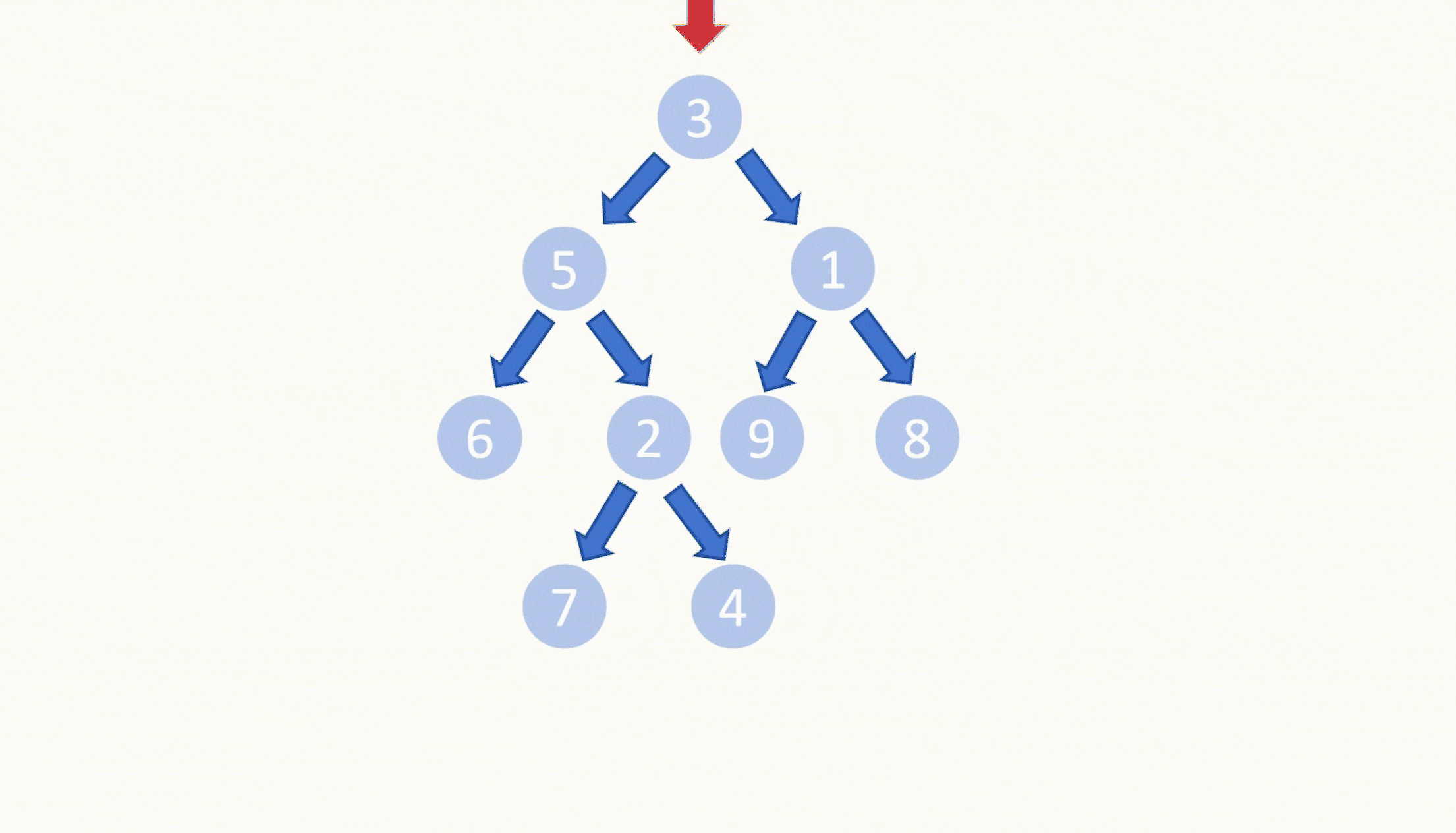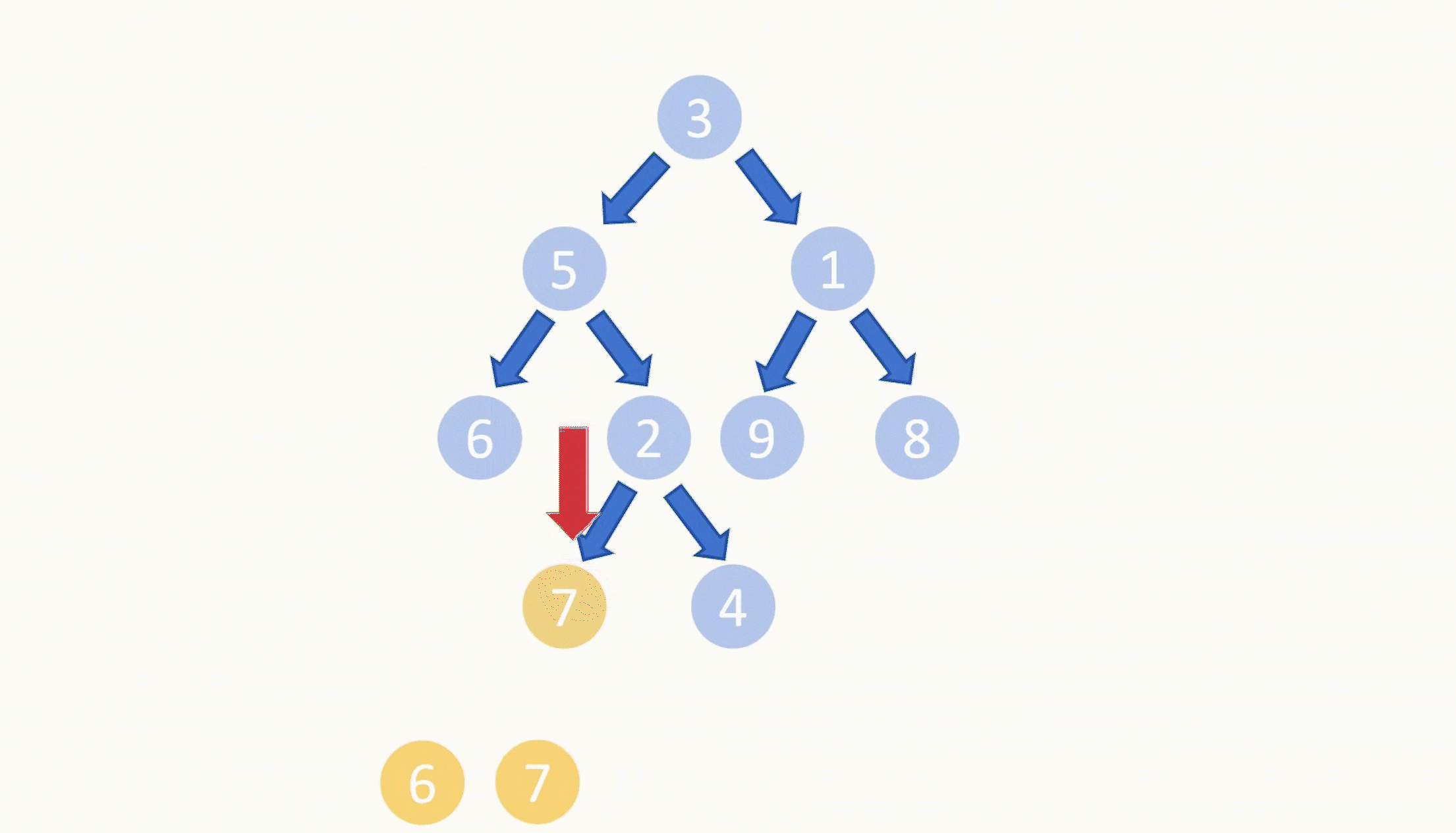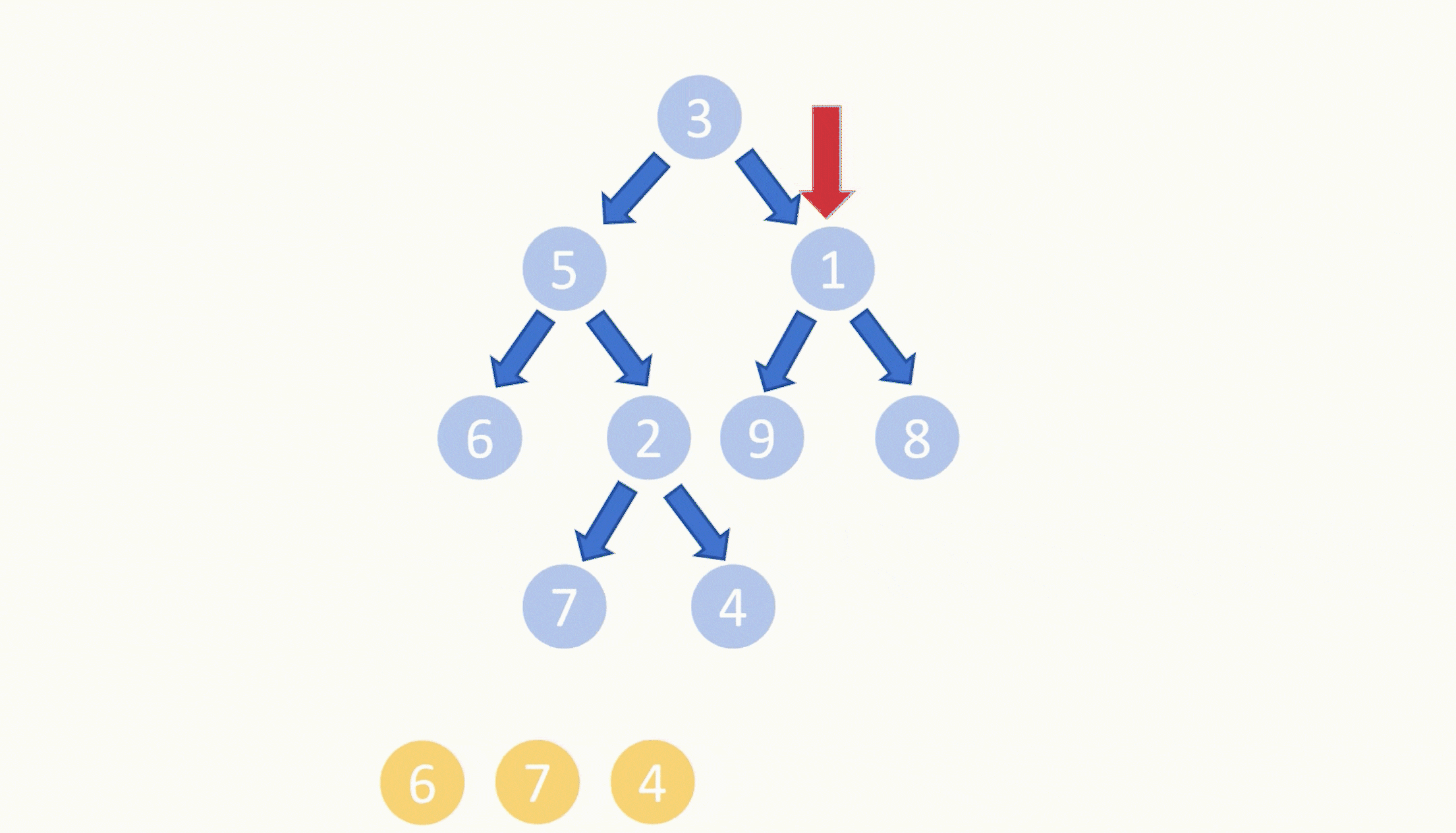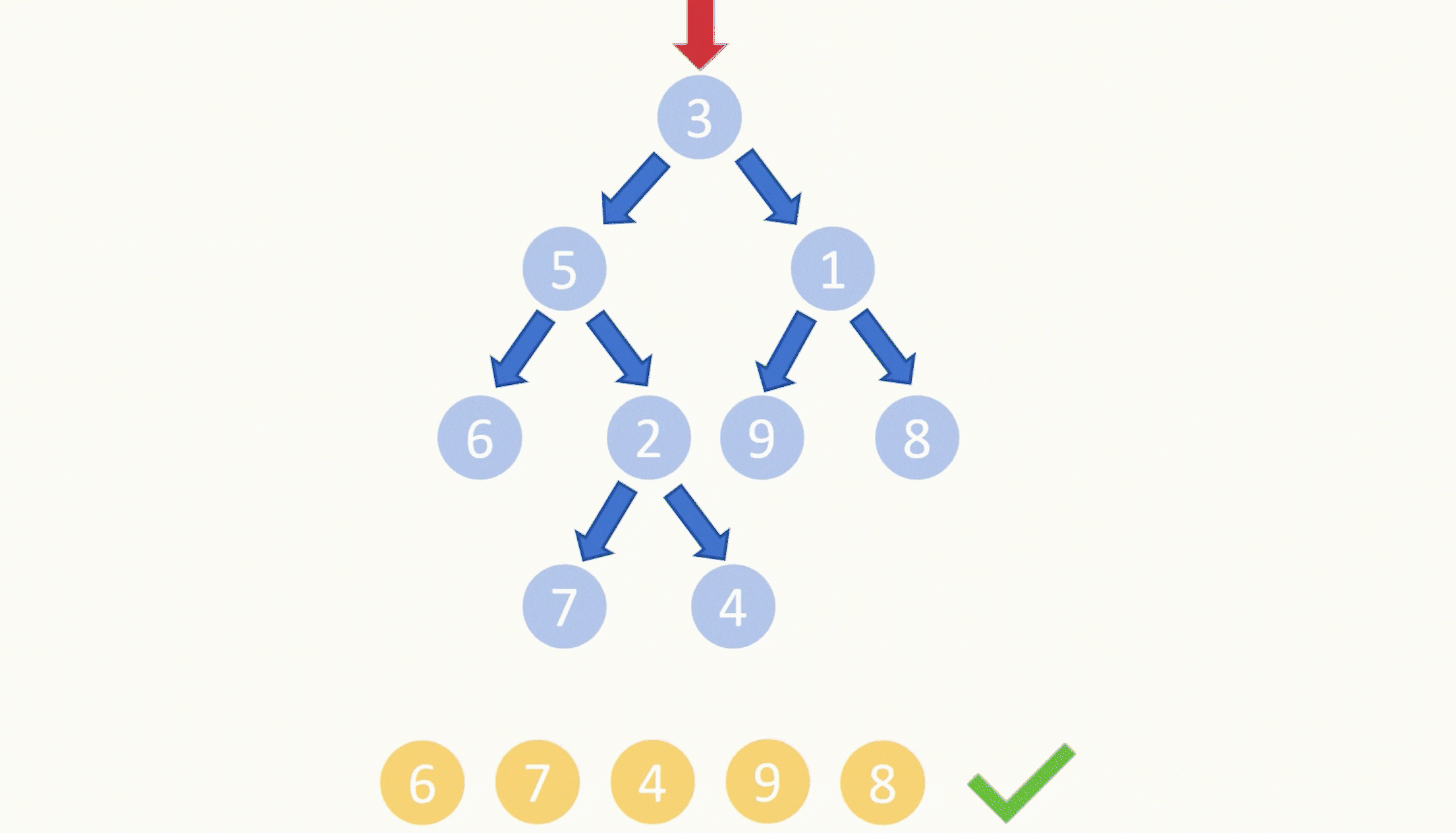
想法：先直接中序遍历（升序的序列）过程中相邻两个数的差值取min，自己写一次AC代码：

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:int min_ans;int ok = 0;   //全局遍历 第一个元素特殊处理！TreeNode* old;   //全局遍历！int search(TreeNode* root)  // 返回前一个节点的val{if(!root) return root->val;int ans1 = 0xffff;int ans2 = 0xffff;if(root->left)ans1 = search(root->left);int tmpval = root->val;cout << tmpval << endl;if(ok)min_ans = min(min_ans,abs(tmpval - old->val));old = root;ok=1;if(root->right)ans2 = search(root->right);return tmpval;}int getMinimumDifference(TreeNode* root) {// 想法：先直接中序遍历（升序的序列）相邻两个数的差值取minmin_ans = INT_MAX;ok=0;search(root);return min_ans;}
};

看了题解，思路和我的一样，但是写法更加简单(设置old起始为null，非null表示非第一次，并且后一步每次都更新old )，学习并写一遍AC代码：

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:int ans = INT_MAX;TreeNode* old =  NULL;void search(TreeNode* root){if(root == NULL)return;search(root->left);if(old)ans = min(ans,abs(root->val - old->val));old = root;search(root->right);}int getMinimumDifference(TreeNode* root) {search(root);return ans;}
};

 2 501. 二叉搜索树中的众数

501. 二叉搜索树中的众数

如果拿一个数组存中序遍历结果很容易，但是题目进阶要求：不要额外的空间。有一些麻烦的思路，比如全局变量维护max的值与数目，每次函数都传递当前值和数目的参数（题解证明不用传参 直接全局变量更新新的cnt即可），不确定能不能实现，然后看题解：

• 知道了普通二叉树的做法时候：最直观的方法一定是把这个树都遍历了，用map统计频率，把频率排个序（有的同学可能可以想直接对map中的value排序，还真做不到，C++中如果使用std::map或者std::multimap可以对key排序，但不能对value排序。所以要把map转化数组即vector，再进行排序，当然vector里面放的也是pair<int, int>类型的数据，第一个int为元素，第二个int为出现频率。），最后取前面高频的元素的集合。
• 在递归遍历二叉搜索树的过程中，介绍了一个统计最高出现频率元素集合的技巧， 要不然就要遍历两次二叉搜索树才能把这个最高出现频率元素的集合求出来。为什么没有这个技巧一定要遍历两次呢？ 因为要求的是集合，会有多个众数，如果规定只有一个众数，那么就遍历一次稳稳的了。和我的思路差不多，就是把我模糊的想法落地了。

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:int cnt = INT_MIN;int maxcnt = INT_MIN;TreeNode* old = NULL;vector<int> ans;void search(TreeNode* root){if(root == NULL)return;search(root->left);// 计算当前cntif(!old)cnt = 1;else{if(root->val == old->val)cnt++;else  //新的元素cnt = 1;}// 计算最大的cnt 和 更新结果if(cnt > maxcnt){maxcnt = cnt;ans.clear();ans.push_back(root->val);}else if(cnt == maxcnt)ans.push_back(root->val);old = root;search(root->right);}vector<int> findMode(TreeNode* root) {search(root);return ans;}
};

3 236. 二叉树的最近公共祖先

236. 二叉树的最近公共祖先

我一开始写了一个递归的版本，其实只用了递归但没有迭代，结果在第29个测试点超出内存限制，不知道是不是TLE，如下：

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode(int x) : val(x), left(NULL), right(NULL) {}* };*/
class Solution {
public:vector<vector<TreeNode*>> ans;void search(TreeNode* root, TreeNode* p, TreeNode* q,vector<TreeNode*> path){if(root == p || root == q)  // 获得结果并不returnans.push_back(path);if(!root->left && !root->right)return;path.push_back(root->left);if(root->left)search(root->left,p,q,path);path.pop_back();path.push_back(root->right);if(root->right)search(root->right,p,q,path);path.pop_back();}TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {//我的思路 写一个函数找到p和q的祖宗路线存在来然后对比两个序列即可。vector<TreeNode*> path;path.push_back(root);search(root , p , q ,path);int i = 0;for(; i < ans[0].size();i++)if(ans[0][i] != ans[1][i])return ans[0][i-1];return ans[0][i-1];}
};

看了题解，正确的思路应该是不止递归，更要好好用到回溯==》后序遍历，基本逻辑是：

• 如果当前节点是p，是q，或者是空直接返回当前节点。（想象如果p是q的父节点 这里的直接return也是满足要求的！！！）
• 后序遍历后：

1. 左子树如果没有pq，右子树也没有pq，就return 空
2. 左子树如果没有pq，右子树有pq，就返回右子树的结果
3. 左子树如果有pq，右子树没有pq，就返回左子树的结果
4. 左右都有的话，说明当前节点就是最近的公共父节点！！！！！！！

我感觉这个写法还是比较妙的写法，有一些一个变量表达2个含义的感觉，没有冗余的东西AC代码：

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode(int x) : val(x), left(NULL), right(NULL) {}* };*/
class Solution {
public:TreeNode* search(TreeNode* root, TreeNode* p, TreeNode* q){if(root == p || root == q || root == NULL)  // 获得结果并不returnreturn root;TreeNode* left = search(root->left,p,q);TreeNode* right = search(root->right,p,q);if(left && right)return root;else if(left && !right)return left;else if(!left && right)return right;else return NULL;}TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {return search(root , p , q );}
};

---

总结：

这一节累计用时2h。

---