图解算法--排序算法

目录

1.冒泡排序算法

2.选择排序算法

3.插入排序算法

4.希尔排序算法

5.归并排序算法

6.快速排序算法

1.冒泡排序算法

原理讲解：

  1. 从待排序的数组中的第一个元素开始，依次比较当前元素和它相邻的下一个元素的大小。
  2. 如果当前元素大于相邻元素，则交换这两个元素的位置，将较大的元素向后冒泡。
  3. 继续比较相邻元素，重复以上步骤，直到遍历完整个数组。
  4. 一轮遍历完成后，最大的元素将会排在最后面。
  5. 重复执行上述步骤，每次遍历都将会使待排序的元素中最大的元素冒泡到正确的位置，直到所有元素都有序排列。

 传统的冒泡排序算法

package Sort.Bubble;import java.util.Arrays;public class javaDemo {public static void main(String[] args) {int nums[] = new int[]{1,4,36,7,42,2,12,5,2};int temp;
//        冒泡算法for (int i=0;i< nums.length-1;i++){for (int j=0;j< nums.length-i-1;j++){if (nums[j]>nums[j+1]){temp = nums[j];nums[j] = nums[j+1];nums[j+1] = temp;}}}System.out.println(Arrays.toString(nums));}
}

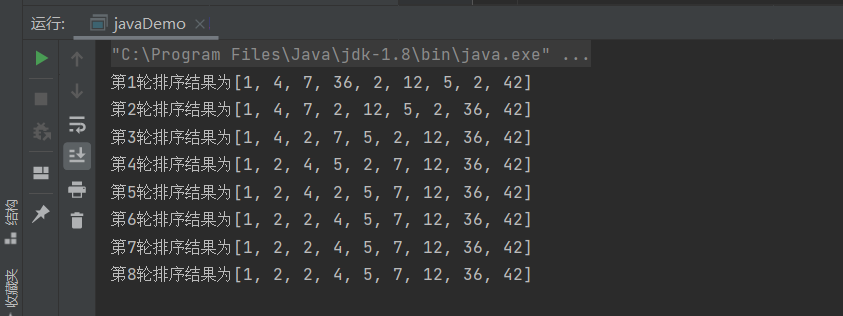
传统的排序算法有个缺点，那就是不管数据是否已经完成排序都会固定执行n(n-1)/2次，而如果加入岗哨的概念进行改造冒泡排序算法就可以提高程序的执行效率

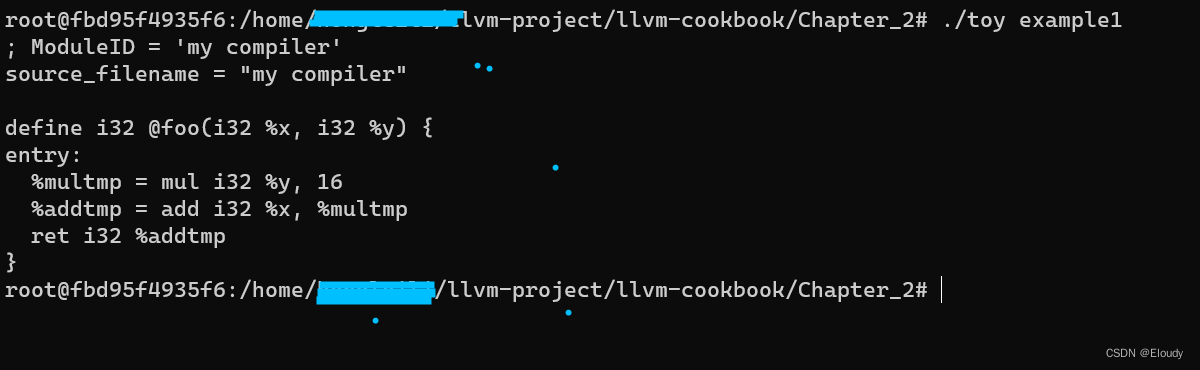
传统冒泡执行已经快要排序好的数组结果如下：

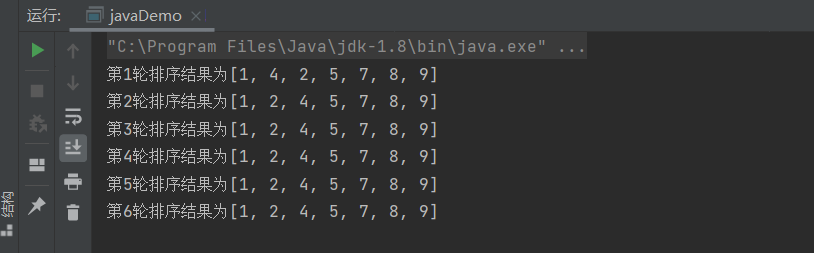
可以看到在第二轮时候就已经排序好了，但是还是不断进行遍历，所以加入一个岗哨（flag）判断功能，当第三轮时候，如果没有元素进行交换后直接退出排序 。

改进型冒泡排序法

package Sort.Bubble;import java.util.Arrays;public class Sentry {public static void main(String[] args) {int num[] = new int[]{1,4,5,2,7,8,9};int flag;int temp;for (int i= num.length-1;i>0;i--){flag = 0;
//            如果发生了交换则不跳出for (int j=0;j<i-1;j++){if (num[j]>num[j+1]){temp = num[j];num[j] = num[j+1];num[j+1] = temp;flag ++;}}
//            如果从头遍历结束都没有交换则直接退出if (flag == 0){break;}System.out.println("第"+(num.length-i)+"轮排序结果为"+ Arrays.toString(num));}}
}

 算法分析：

  • 冒泡排序算法在最坏的情况下时间复杂度是O(n^2)
  • 在最好的情况下时间复杂度是O(n)

2.选择排序算法

原理讲解： 

  1. 遍历待排序的数组，将第一个元素作为当前最小值。
  2. 从当前位置之后的元素中找到最小的元素，并记录其位置。
  3. 如果找到了比当前最小值更小的元素，则将该元素的位置更新为当前最小值的位置。
  4. 遍历完整个数组后，将最小值与当前位置的元素进行交换。
  5. 继续从下一个位置开始重复以上步骤，直到遍历完整个数组。

案例代码

package Sort.Chose.chose;import java.util.Arrays;public class javaDemo {public static void main(String[] args) {int nums[] = new int[]{1,2,4,2,3,51,12,6,2};int min;int index;int temp;for (int i=0;i< nums.length-1;i++){
//            每一轮初始化最小值与最小值下角标min = nums[i];index = i;for (int j=i+1;j< nums.length;j++){if (min>nums[j]){min = nums[j];index = j;}}temp = nums[i];nums[i] = min;nums[index] = temp;}System.out.println(Arrays.toString(nums));}
}

 算法分析：

  • 冒泡排序算法无论在最坏还是最好的情况下时间复杂度都是O(n^2)

3.插入排序算法

 原理讲解：

  1. 将数组分为已排序和未排序两部分。一开始，将第一个元素视为已排序部分，其余元素视为未排序部分。
  2. 从未排序部分选择第一个元素，依次与已排序部分的元素比较。
  3. 如果选取的元素小于已排序部分的某个元素，则将该元素插入到正确的位置，同时将已排序部分中的元素向后移动一位。
  4. 重复上述步骤，将未排序部分的每个元素逐个插入到已排序部分的正确位置。
  5. 当所有元素都插入完成，即未排序部分为空时，排序完成。

案例代码  

package Sort.InsertSort;import java.util.Arrays;public class javaDemo {public static void main(String[] args) {int nums[] = new int[]{4,1,5,2,6,7,2};int temp;for (int i=0;i< nums.length;i++){for (int j=0;j<i;j++){if (nums[i]<nums[j]){temp = nums[j];nums[j] = nums[i];nums[i] = temp;}}System.out.println("第"+(i+1)+"轮排序结果为"+ Arrays.toString(nums));}}
}

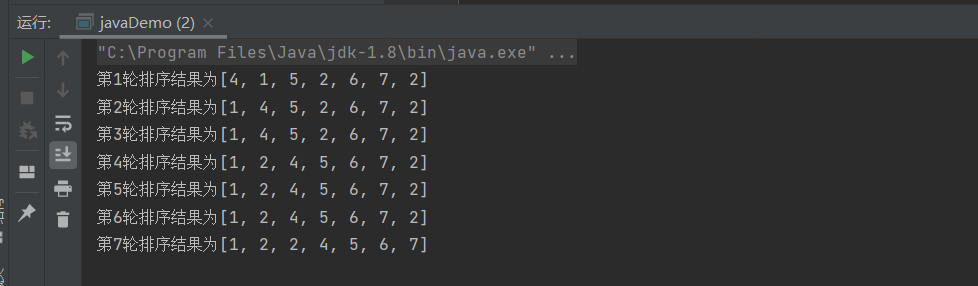
算法分析：

  • 冒泡排序算法在最坏的情况下时间复杂度是O(n^2)
  • 在最好的情况下时间复杂度是O(n)

4.希尔排序算法

  原理讲解：

  1. 首先，选择一个增量 gap，通常将数组长度的一半作为初始增量。
  2. 将数组按照增量进行分组，并对每个分组使用插入排序算法进行排序。
  3. 逐渐缩小增量，重复以上步骤，直到增量为 1。
  4. 最后使用增量为 1 的插入排序对整个数组进行最后一次排序

案例代码：

package Sort.Shell;import java.util.Arrays;public class ShellSort {public static void main(String[] args) {int[] arr = {9, 5, 2, 7, 1, 8, 3, 6, 4};int n = arr.length;// 定义增量序列int[] increments = {5, 3, 1};System.out.println("原始数组顺序为"+Arrays.toString(arr));// 遍历增量序列for (int increment : increments) {// 对每个增量进行插入排序for (int i = increment; i < n; i++) {int temp = arr[i];int j = i;// 在当前增量下，对子序列进行插入排序while (j >= increment && arr[j - increment] > temp) {arr[j] = arr[j - increment];j -= increment;}arr[j] = temp;System.out.println("当前增量为"+increment+"，当前数组为："+Arrays.toString(arr));}}}
}

算法分析：

  • 希尔排序算法无论在最坏还是最好的情况下时间复杂度都是O(n^3/2)
  • 空间最优解

5.归并排序算法

   原理讲解：

  1. 将待排序的数组递归地分成两个子数组，直到每个子数组只有一个元素。
  2. 对每个子数组进行合并操作，将两个有序的子数组合并成一个有序的数组。
  3. 重复以上步骤，直到所有的子数组都被合并成一个完整的有序数组。

案例代码：

package Sort.MergeSort;import java.util.Arrays;public class mergeSort {public static void mergeSort(int[] arr) {if (arr == null || arr.length <= 1) {return;}int[] temp = new int[arr.length];mergeSort(arr, 0, arr.length - 1, temp);}private static void mergeSort(int[] arr, int left, int right, int[] temp) {if (left < right) {int mid = left + (right - left) / 2;mergeSort(arr, left, mid, temp); // 递归排序左半部分mergeSort(arr, mid + 1, right, temp); // 递归排序右半部分merge(arr, left, mid, right, temp); // 合并左右两个有序数组}System.out.println("当前顺序为"+Arrays.toString(arr));}private static void merge(int[] arr, int left, int mid, int right, int[] temp) {int i = left; // 左半部分起始索引int j = mid + 1; // 右半部分起始索引int k = 0; // 临时数组索引// 将左右两个有序数组按顺序合并到temp数组中while (i <= mid && j <= right) {if (arr[i] <= arr[j]) {temp[k++] = arr[i++];} else {temp[k++] = arr[j++];}}// 处理剩余的元素while (i <= mid) {temp[k++] = arr[i++];}while (j <= right) {temp[k++] = arr[j++];}// 将临时数组的元素拷贝回原数组for (i = 0; i < k; i++) {arr[left + i] = temp[i];}}public static void main(String[] args) {int[] arr = {9, 5, 2, 7, 1, 8, 3, 6, 4};System.out.println("原始数组："+ Arrays.toString(arr));mergeSort(arr);}
}

算法分析：

  • 归并排序算法无论在最坏还是最好的情况下时间复杂度都是O(nlogn)

6.快速排序算法

   原理讲解：

  1. 选择一个基准元素（通常是数组的第一个或最后一个元素）作为参考点。
  2. 将待排序的数组分成两个子数组，其中一个子数组中的元素小于等于基准元素，另一个子数组中的元素大于基准元素。
  3. 对这两个子数组分别重复上述步骤，递归地进行快速排序。
  4. 当子数组的长度为 1 或 0 时，递归终止。
  5. 将排序好的子数组合并起来，即可得到完整的有序数组。

案例代码：

package Sort.Quick;import java.util.Arrays;public class QuickSort {public static void quickSort(int[] arr) {if (arr == null || arr.length <= 1) {return;}quickSort(arr, 0, arr.length - 1);}private static void quickSort(int[] arr, int low, int high) {if (low < high) {int pivotIndex = partition(arr, low, high); // 将数组划分为两部分，返回中轴元素的索引quickSort(arr, low, pivotIndex - 1); // 递归排序左半部分quickSort(arr, pivotIndex + 1, high); // 递归排序右半部分}System.out.println("当前数组为"+Arrays.toString(arr));}private static int partition(int[] arr, int low, int high) {int pivot = arr[low]; // 选择第一个元素作为中轴元素int left = low;int right = high;while (left < right) {// 从右向左找第一个小于等于中轴元素的位置while (left < right && arr[right] >= pivot) {right--;}if (left < right) {arr[left] = arr[right];left++;}// 从左向右找第一个大于中轴元素的位置while (left < right && arr[left] <= pivot) {left++;}if (left < right) {arr[right] = arr[left];right--;}}arr[left] = pivot; // 将中轴元素放置到最终位置return left; // 返回中轴元素的索引}public static void main(String[] args) {int[] arr = {9, 5, 2, 7, 1, 8, 3, 6, 4};System.out.printf("原始数组：");System.out.println(Arrays.toString(arr));quickSort(arr);}
}

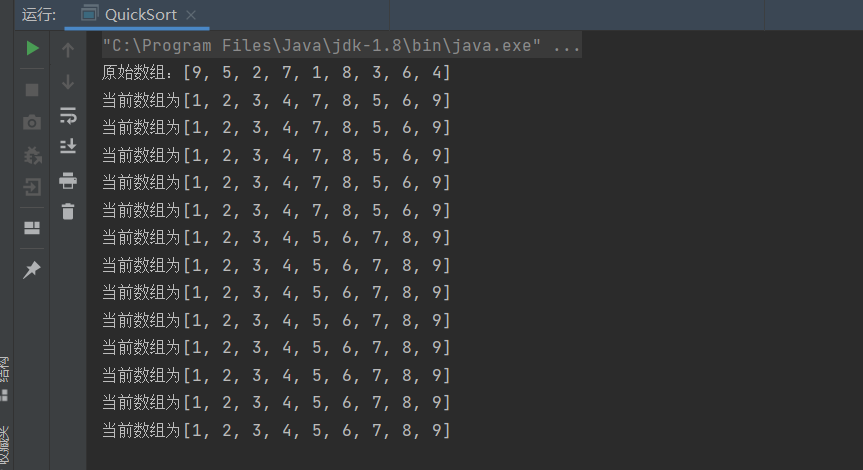
 算法分析：

  • 快速排序算法在最坏的情况下时间复杂度是O(nlog2n)
  • 在最好的情况下时间复杂度是O(n)
  • 公认最好的排序算法

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.rhkb.cn/news/101608.html

如若内容造成侵权/违法违规/事实不符，请联系长河编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

剪枝基础与实战(1): 概述

剪枝基础与实战(1): 概述

本文介绍基于L1正则化的剪枝原理，并以VGG网络进行实战说明。将从零详细介绍模型训练、稀疏化、剪枝、finetune的全过程，提供详细的源码及说明，有助于对剪枝的熟练掌握，后续也会对yolov8进行剪枝的介绍。 论文: Learning Efficient Convolutional Networks through Network …
阅读更多...
SpringBoot项目（支付宝整合）——springboot整合支付宝沙箱支付 从极简实现到IOC改进

SpringBoot项目（支付宝整合）——springboot整合支付宝沙箱支付 从极简实现到IOC改进

目录 引出git代码仓库准备工作支付宝沙箱api内网穿透 [natapp.cn](https://natapp.cn/#download) springboot整合—极简实现版1.导包配置文件2.controller层代码3.进行支付流程4.支付成功回调 依赖注入的改进1.整体结构2.pom.xml文件依赖3.配置文件4.配置类&#xff0c;依赖注入…
阅读更多...
渗透测试方法论

渗透测试方法论

文章目录 渗透测试方法论1. 渗透测试种类黑盒测试白盒测试脆弱性评估 2. 安全测试方法论2.1 OWASP TOP 102.3 CWE2.4 CVE 3. 渗透测试流程3.1 通用渗透测试框架3.1.1 范围界定3.1.2 信息搜集3.1.3 目标识别3.1.4 服务枚举3.1.5 漏洞映射3.1.6 社会工程学3.1.7 漏洞利用3.1.8 权…
阅读更多...
根据源码，模拟实现 RabbitMQ - 虚拟主机 + Consume设计 (7)

根据源码，模拟实现 RabbitMQ - 虚拟主机 + Consume设计 (7)

目录 一、虚拟主机 Consume设计 1.1、承接问题 1.2、具体实现 1.2.1、消费者订阅消息实现思路 1.2.2、消费者描述自己执行任务方式实现思路 1.2.3、消息推送给消费者实现思路 1.2.4、消息确认 一、虚拟主机 Consume设计 1.1、承接问题 前面已经实现了虚拟主机大部分功…
阅读更多...
【linux】2 Linux编译器-gcc/g++和Linux调试器-gdb

【linux】2 Linux编译器-gcc/g++和Linux调试器-gdb

文章目录 一、Linux编译器-gcc/g使用1.1 背景知识1.2 gcc如何完成1.3 函数库1.4 gcc选项 二、linux调试器-gdb使用2.1 背景2.2 开始使用 总结 ヾ(๑╹◡╹)&#xff89;" 人总要为过去的懒惰而付出代价ヾ(๑╹◡╹)&#xff89;" 一、Linux编译器-gcc/g使用 1.1 背景…
阅读更多...
JS加密的域名锁定功能，JShaman支持泛域名

JS加密的域名锁定功能，JShaman支持泛域名

JShaman的域名锁定功能&#xff0c;支持泛域名 JShaman的JS代码混淆加密中&#xff0c;有一项“域名锁定”功能。使用此功能后&#xff0c;代码运行时会检测浏览器地址中的域名信息&#xff0c;如是非指定域名&#xff0c;则不运行&#xff0c;以此防止自己网站的JS代码被复制…
阅读更多...
python的文件操作

python的文件操作

前言 打印内容到屏幕 最简单的输出方式是调用print函数&#xff0c;此函数会将你传递的表达式转化成字符串表达式&#xff0c;并将结果写道标准输出中。 读取键盘输入 python提供了两个raw_input和input内置函数从标准输入中读取一行文本&#xff0c;默认的标准输入是键盘。 …
阅读更多...
Android NDK JNI与Java的相互调用

Android NDK JNI与Java的相互调用

一、Jni调用Java代码 jni可以调用java中的方法和java中的成员变量，因此JNIEnv定义了一系列的方法来帮助我们调用java的方法和成员变量。 以上就是jni调用java类的大部分方法，如果是静态的成员变量和静态方法，可以使用***GetStaticMethodID、CallStaticObjectMethod等***。就…
阅读更多...
docker安装fastDFS

docker安装fastDFS

一、docker安装 1、搜索镜像 2、拉取镜像 最新版本&#xff1a; docker pull delron/fastdfs3、使用镜像构建容器 3.1 创建tracker容器 docker run -dti --networkhost --name my-tracker -v /opt/zdxf/soft/fastdfs/tracker:/var/fdfs -v /etc/localtime:/etc/localtime d…
阅读更多...
Nvidia Jetson 编解码开发（3）解决H265解码报错“PPS id out of range”

Nvidia Jetson 编解码开发（3）解决H265解码报错“PPS id out of range”

1.问题描述 基于之前的开发程序 Nvidia Jetson 编解码开发（2）Jetpack 4.x版本Multimedia API 硬件编码开发--集成encode模块_free-xx的博客-CSDN博客 通过Jetson Xavier NX 硬编码的H265发出后， 上位机断点播放发出来的H265码流， 会报“PPS id out of range” 错误 …
阅读更多...
【C语言】喝汽水问题

【C语言】喝汽水问题

大家好&#xff01;今天我们来学习C语言中的喝汽水问题&#xff01; 目录 1. 题目内容&#xff1a; 2. 思路分析 2.1 方法一 2.2 方法二 2.3 方法三 3. 代码实现 3.1 方法一 3.2 方法二 3.3 方法三 1. 题目内容 喝汽水&#xff0c;1瓶汽水1元&#xff0c;2个空瓶可以…
阅读更多...
算法题面试实战收集

算法题面试实战收集

回文数字 2023-08-18 美团 一面 在不使用额外的内存空间的条件下判断一个整数是否是回文。 回文指逆序和正序完全相同。 数据范围&#xff1a; 进阶&#xff1a; 空间复杂度O(1) &#xff0c;时间复杂度 O(n) 提示&#xff1a; 负整数可以是回文吗&#xff1f;&#xff08;比如…
阅读更多...
vue项目配置git提交规范

vue项目配置git提交规范

vue项目配置git提交规范 一、背景介绍二、husky、lint-staged、commitlint/cli1.husky2.lint-staged3.commitlint/cli 三、具体使用1.安装依赖2.运行初始化脚本3.在package.json中配置lint-staged4.根目录新增 commitlint.config.js 4.提交测试1.提示信息格式错误时2.eslint校验…
阅读更多...
深度学习3：激活函数

深度学习3：激活函数

一、激活函数的简介与由来 激活函数&#xff1a;是用来加入非线性因素的&#xff0c;解决线性模型所不能解决的问题。 线性函数的组合解决的问题太有限了&#xff0c;碰到非线性问题就束手无策了。如下图。 通过激活函数映射之后&#xff0c;可以输出非线性函数。 最后再通过…
阅读更多...
【2023深圳杯数学建模A题思路模型与代码分享】

【2023深圳杯数学建模A题思路模型与代码分享】

2023深圳杯数学建模A题 A题 影响城市居民身体健康的因素分析解题思路第一问第二问第三问第四问 技术文档第一问完整代码写在最后 A题 影响城市居民身体健康的因素分析 以心脑血管疾病、糖尿病、恶性肿瘤以及慢性阻塞性肺病为代表的慢性非传染性疾病&#xff08;以下简称慢性病…
阅读更多...
【Terraform学习】使用 Terraform 托管 S3 静态网站（Terraform-AWS最佳实战学习）

【Terraform学习】使用 Terraform 托管 S3 静态网站（Terraform-AWS最佳实战学习）

使用 Terraform 托管 S3 静态网站 实验步骤 前提条件 安装 Terraform&#xff1a; 地址 下载仓库代码模版 本实验代码位于 task_s3 文件夹中。 变量文件 variables.tf 在上面的代码中&#xff0c;您将声明&#xff0c;aws_access_key&#xff0c;aws_secret_key和区域变量…
阅读更多...
ubuntu 22.04 LTS 在 llvm release/17.x 分支上编译 cookbook llvm example Chapter 02

ubuntu 22.04 LTS 在 llvm release/17.x 分支上编译 cookbook llvm example Chapter 02

不错的资料&#xff1a; LLVMClang编译器链接器--保值【进阶之路二】 - 掘金 —————————————————————————————————————— 下载 llvm-cookbook example: $ git clone https://github.com/elongbug/llvm-cookbook.git 也可以参照llvm-pr…
阅读更多...
【BASH】回顾与知识点梳理（三十九）

【BASH】回顾与知识点梳理（三十九）

【BASH】回顾与知识点梳理 三十九 三十九. make、tarball、函数库及软件校验39.1 用 make 进行宏编译为什么要用 makemakefile 的基本语法与变量 39.2 Tarball 的管理与建议使用原始码管理软件所需要的基础软件Tarball 安装的基本步骤一般 Tarball 软件安装的建议事项 (如何移除…
阅读更多...
【vue3+ts项目】配置eslint校验代码工具，eslint+prettier+stylelint

【vue3+ts项目】配置eslint校验代码工具，eslint+prettier+stylelint

1、运行好后自动打开浏览器 package.json中 vite后面加上 --open 2、安装eslint npm i eslint -D3、运行 eslint --init 之后&#xff0c;回答一些问题&#xff0c; 自动创建 .eslintrc 配置文件。 npx eslint --init回答问题如下&#xff1a; 使用eslint仅检查语法&…
阅读更多...
6-模板初步使用

6-模板初步使用

官网: 中文版: 介绍-Jinja2中文文档 英文版: Template Designer Documentation — Jinja Documentation (2.11.x) 模板语法 1. 模板渲染 (1) app.py 准备数据 import jsonfrom flask import Flask,render_templateimport settingsapp Flask(__name__) app.config.from_obj…
阅读更多...
最新文章
推荐文章

Copyright @ 2022~2023