1.概念

1.排序的稳定性

常见的稳定的排序有三种：直接插入排序，冒泡排序，归并排序

对于一组数据元素排列，使用某种排序算法对它进行排序，若相同数据之间的前后位置排序后和未排序之前是相同的，我们就成这种排序算法具有稳定性

单看单个属性的稳定性并无意义，稳定性主要体现在对具有多个属性的对象进行排序时才有意义
假设一个订单对象有两个属性，分别是下单时间与下单金额：
此时我们有一个需求，就是按照订单金额从高到低排序，若金额相同，则按照下单的先后时间排序

• 方法一：就是先按照顺序排序，然后把金额相同的订单再次按照时间排序，但是这样就需要多次排序
• 方法二：如果我们先把订单按照下单时间的先后排好序，然后再按照订单金额排序，此时如果我们使用的排序是稳定性的，那么它排序后同样是按照下单顺序先后排列的，此时我们就只需要两次排序

所以排序的稳定性也是非常重要的

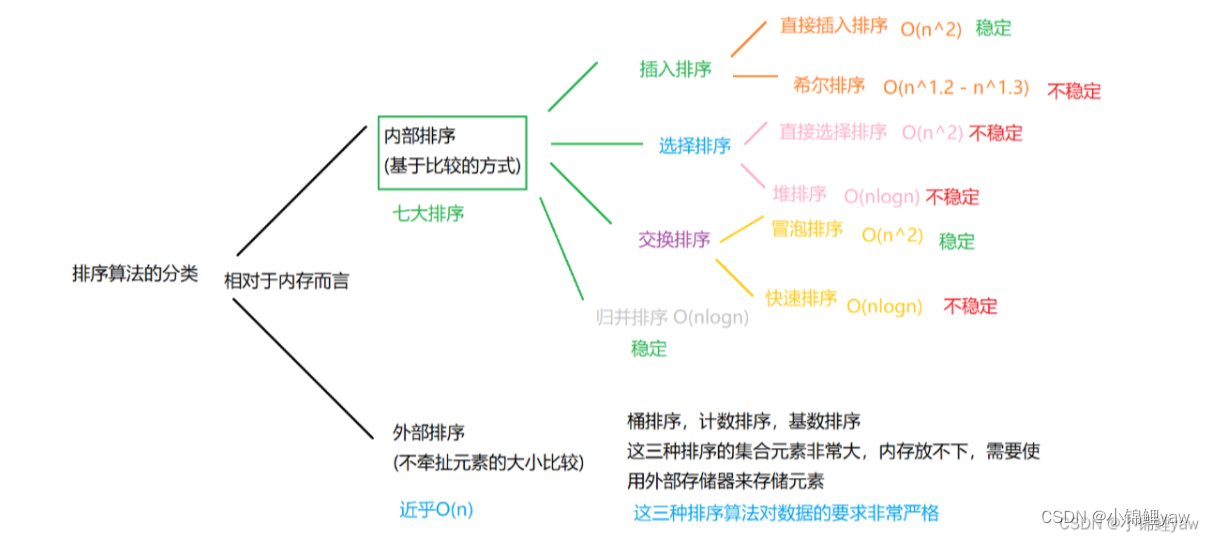
2.排序分类

1.外部排序（不牵扯元素大小比较）

外部排序主要有，桶排序，计数排序，基数排序，时间复杂度近乎O(n)
这三种排序的集合元素非常大，内存放不下，需要使用外部存储器来存储排序,并且对数据的要求非常严格

2.内部排序（基于比较的方式）

1.插入排序

⭐直接插入排序（稳定）

1.核心思路

每次从无序区间中选择第一个元素，插入到有序区间的合适位置（相当于打扑克牌码牌的过程），有序区间+1，无序区间-1，直至整个数组有序

⭐⭐⭐直接插入排序在近乎有序的集合性能上非常好（是因为近乎有序的集合，不需要频繁的去交换），常常作为其他高阶排序的优化手段

2.详细代码

    /*** 直接插入排序* @param nums*/public static void insertSort(int[] nums) {// 有序区间[0,i)// 无序区间[i,n)for (int i = 1; i < nums.length; i++) {for (int j = i; j-1 >= 0; j--) {// 若当前值比前一个位置值还小，交换位置if (nums[j] < nums[j-1]) {swap(nums, j , j-1);}}}}

⭐希尔排序

希尔排序是对插入排序的优化，因为插入排序在近乎有序的数组上性能很好，希尔排序正是利用了这一点

1.核心思路

希尔排序不断地将原数组分为若干个子数组，先将子数组内部调整为有序，不断变大分组的长度，当分组长度为1时（一个元素天然有序），此时进行一次插入排序即可

2.详细代码

   // 希尔排序public static void shellSort(int[] arr) {int gap = arr.length >> 1;while (gap > 1) {// 先按照gap分组，组内使用插入排序insertionSortByGap(arr,gap);gap = gap >> 1;}// 当gap == 1时，整个数组接近于有序，此时来一个插入排序insertionSortByGap(arr,1);}// 按照gap分组，组内的插入排序private static void insertionSortByGap(int[] arr, int gap) {// i初始化为0也可以，更容易理解for (int i = gap; i < arr.length; i++) {for (int j = i; j - gap >= 0 && arr[j] < arr[j - gap] ; j -= gap) {swap(arr,j,j - gap);}}}

2.选择排序

⭐直接选择排序（不稳定）

1.核心思路

每次在无序区间选择最小值与无序区间第一个位置元素交换，有序区间+1，无序区间-1,直至整个数组有序

2.详细代码

    /*** 直接选择排序* @param nums*/public static void selectionSort(int[] nums) {// 起始状态:有序区间[0,i)// 无需区间[i,n)for (int i = 0; i < nums.length - 1; i++) {// 指向当前无需区间最小值的下标int minIndex = i;for (int j = i+1; j < nums.length; j++) {// 若当前值比最小值还小if (nums[j] < nums[minIndex]) {// 更新最小值下标minIndex = j;}}// 此时minIndex指向无需区间的最小值，将其加载有序区间的后面，有序区间+1，无序区间-1swap(nums, i, minIndex);}}

⭐堆排序

堆排详情博客：
原地堆排序

3.交换排序

⭐冒泡排序（稳定）

1.核心思路

每次遍历将无序数组的最大元素交换至末尾，无序数组-1，有序数组+1，直至整个数组有序

2.详细代码

    // 无序区间[0...i]// 有序区间[]public static void bubbleSort(int[] arr) {// 外层循环表示要进行元素操作的趟数for (int i = 0; i < arr.length - 1; i++) {boolean isSwaped = false;for (int j = 0; j < arr.length - i - 1; j++) {if (arr[j] > arr[j + 1]) {isSwaped = true;swap(arr,j,j + 1);}}if (!isSwaped) {break;}}}

⭐快速排序（不稳定）

1.核心思路

每次从无序数组中选取一个元素作为分区点（pivot），将原集合中所有<pivot的元素都放在分区点的左侧，将所有>pivot的元素都放在分区点的右侧，这样分区点最终位置就确定了，继续在左半区间和右半区间重复此过程即可

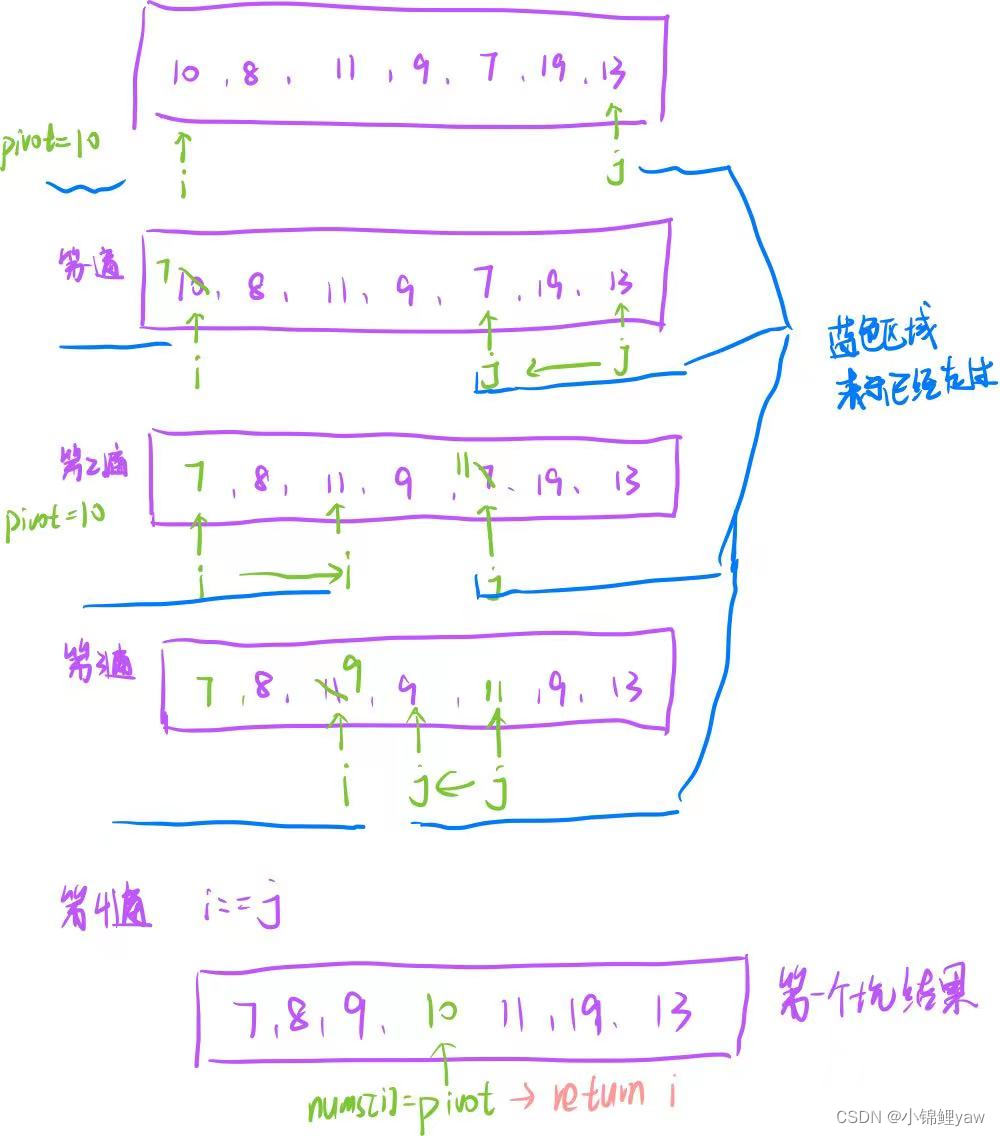
快速排序和直接选择排序不同的是在快排选择的过程中在不断地调整元素的顺序，在这个过程中原数组已经不断有序了

2.详细代码

    /*** 快速排序（挖坑法）*/public static void quitSort(int[] nums) {quitSortInternal(nums, 0, nums.length-1);}private static void quitSortInternal(int[] nums, int l, int r) {if (l >= r) {return;}// 分区之后，返回已经放好位置的元素下标int p = quitSortByHole(nums, l, r);// 将放好位置元素的左侧丢进去排序quitSortInternal(nums, l, p - 1);// 在将放好位置元素的右侧丢进去排序quitSortInternal(nums, p + 1, r);// 此时数组就整体有序了}/*** 使用非递归的方式* @param nums* @param l* @param r*/private static void quitSortInternal1(int[] nums, int l, int r) {Deque<Integer> stack = new ArrayDeque<>();stack.push(r);stack.push(l);while (!stack.isEmpty()) {// 获取左右区间int i = stack.pop();int j = stack.pop();if (i >= j) {continue;}// 调用获得一个位置的结果int p = quitSortByHole(nums, i, j);// 将左边压入栈中stack.push(p-1);stack.push(i);// 右边压入栈中stack.push(j);stack.push(p+1);}}private static int quitSortByHole(int[] nums, int l, int r) {// 分区数字int pivot = nums[l];int i = l;int j = r;while (i < j) {while (i < j && nums[j] >= pivot) {j--;}// 走到这说明nums[j] < pivotnums[i] = nums[j];while (i < j && nums[i] <= pivot) {i++;}// 走到这说明nums[i] > pivotnums[j] = nums[i];}// 出循环说明i==j// 将pivot写回inums[i] = pivot;// 返回分区点最终位置return i;}

4.归并排序

⭐归并排序(稳定，时间复杂度O(nlogn)，空间复杂度O(n))

对原始数据不敏感

1.核心思路

1. 先不断地将原数组一分为二，直至子数组长度为1
2. 不断地将两个相邻的有序子数组合并成一个更大的有序子数组，直至合并后的数组与原数组长度相同，此时排序完成

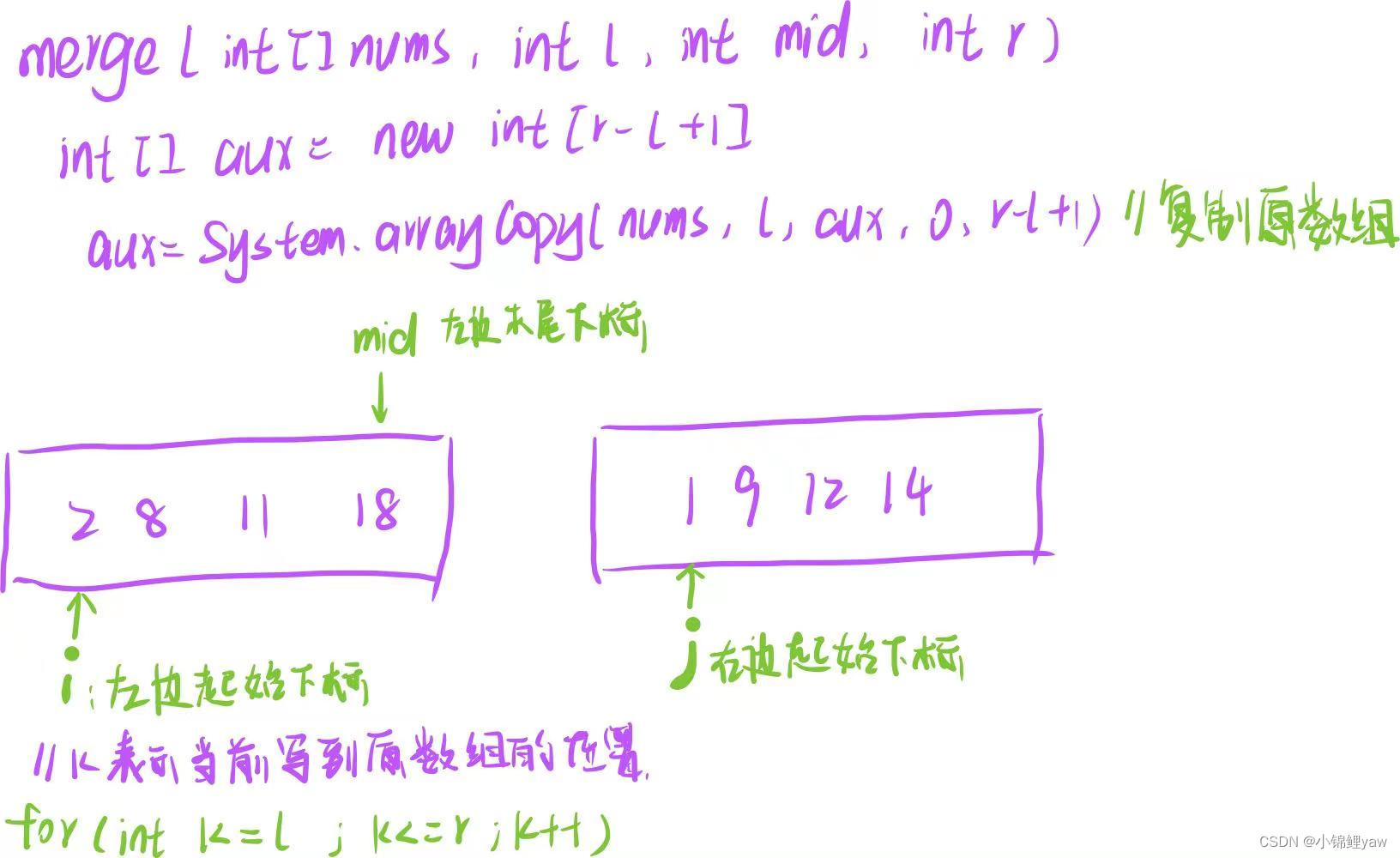
核心操作：合并两个子数组merge（nums, l, mid, r）
int i=l代表左边数组走到的下标，
int j=mid+1代表右边数组走到的下标，
k代表当前原数组合并到哪个位置

2.归并排序应用

3.详细代码

    /*** 归并排序*/public static void mergeSort(int[] nums) {mergeSortInternal(nums, 0, nums.length-1);}/*** 在nums的l-r内进行归并排序* @param nums* @param l* @param r*/private static void mergeSortInternal(int[] nums, int l, int r) {if (l >= r) {return;}int mid = l + ((r - l) >> 1);;// 将左边和右边丢到mergemergeSortInternal(nums, l, mid);mergeSortInternal(nums, mid+1, r);// 此时说明左右两个数组都已经排好序merge(nums, l, mid, r);}private static void merge(int[] nums, int l, int mid, int r) {// 创建一个大小与r-l+1一样大的数组int[] aux = new int[r - l + 1];System.arraycopy(nums, l, aux, 0, r - l + 1);int i = l;int j = mid+1;// i代表左边数组走到的下标，j代表右边数组走到的下标，k代表当前原数组合并到哪个位置for (int k = l; k <= r; k++) {if (i > mid) {// 说明左边的数组已经走完,把右边的全部写回原数组即可nums[k] = aux[j-l];j++;} else if (j > r) {// 说明右边的数组已经走完,把左边的全部写回原数组即可nums[k] = aux[i-l];i++;} else if (aux[i-l] <= aux[j-l]) {// 说明左边的数字小，把左边数组内的数字写回原数组nums[k] = aux[i-l];i++;} else {// 说明右边的数字小，把右边数组内的数字写回原数组nums[k] = aux[j-l];j++;}}}