39.组合总和
分析:同一个数可以选多次,但是不能有重复的答案;
思路:横向遍历,纵向递归(不同的是递归的时候不需要跳到下一个位置,因为同一个数可以选多次)
class Solution {
public:vector<vector<int>>res;vector<int>mids;void backtrace(vector<int>&candidates,int start,int sum,int target){if(sum>=target){//终止条件if(sum==target)//目标条件res.push_back(mids);return;}for(int i=start;i<candidates.size();i++){mids.push_back(candidates[i]);sum+=candidates[i];backtrace(candidates,i,sum,target);//因为同一个数可以选多次,所以递归为imids.pop_back();sum-=candidates[i];}}vector<vector<int>> combinationSum(vector<int>& candidates, int target) {backtrace(candidates,0,0,target);return res;}
};
40.组合总和||
思路:重点在于去重
去重:树层去重,需要在递归遍历的时候判断是否重复
class Solution {
public:vector<vector<int>>res;vector<int>mids;void backtrace(vector<int>&candidates,int startIndex,int sum,int target,vector<bool>&used){if(sum==target){res.push_back(mids);return;}//剪枝for(int i=startIndex;i<candidates.size() && sum+candidates[i]<=target;i++){if(i>0 && candidates[i]==candidates[i-1] && used[i-1]==false)//树层去重continue;mids.push_back(candidates[i]);sum+=candidates[i];used[i]=true;backtrace(candidates,i+1,sum,target,used);used[i]=false;mids.pop_back();sum-=candidates[i];}}vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {sort(candidates.begin(),candidates.end());vector<bool>used(candidates.size(),false);backtrace(candidates,0,0,target,used);return res;}
};
131.分割回文串
思路:分割字符串,然后多了一个判断是否回文的操作
class Solution {
public:vector<vector<string>>res;vector<string>mids;bool judge(const string& s,int left,int right){while(left<right){if(s[left]!=s[right]) return false;left++;right--;}return true;}void backtrace(string&s,int startIndex){if(startIndex>=s.size()){res.push_back(mids);return;}for(int i=startIndex;i<s.size();i++){if(!judge(s,startIndex,i)) continue;//判断是否回文串string str=s.substr(startIndex,i-startIndex+1);mids.push_back(str);backtrace(s,i+1);mids.pop_back();}}vector<vector<string>> partition(string s) {backtrace(s,0);return res;}
};
78.子集
画图分析:
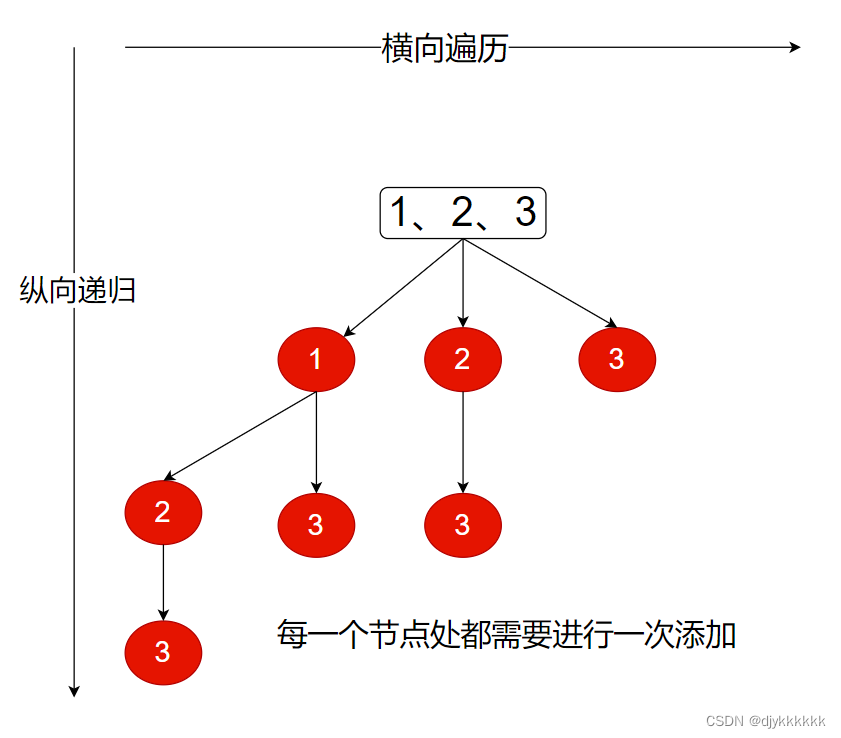
思路:横向遍历,每次遍历的时候都进行一次添加,然后进行纵向递归,递归完之后进行回溯。
class Solution {
public:vector<vector<int>>res;vector<int>mid;void backtrace(vector<int>&nums,int start){res.push_back(mid);if(start==nums.size()){//res.push_back(mid);return;}for(int i=start;i<nums.size();i++){mid.push_back(nums[i]);backtrace(nums,i+1);mid.pop_back();}}vector<vector<int>> subsets(vector<int>& nums) {backtrace(nums,0);return res;}
};
90.子集||
分析:和上题一样,区别在于有重复数字
思路:组合问题有重复都考虑先排序再操作!
class Solution {
public:vector<vector<int>>res;vector<int>mid;void backtrace(vector<int>&nums,int start){if(find(res.begin(),res.end(),mid)==res.end())//去重res.push_back(mid);if(start==nums.size())return;for(int i=start;i<nums.size();i++){mid.push_back(nums[i]);backtrace(nums,i+1);mid.pop_back();}}vector<vector<int>> subsetsWithDup(vector<int>& nums) {sort(nums.begin(),nums.end());//需要排序backtrace(nums,0);return res;}
};
491.递增子序列
思路:重点在于set去重以及递增条件
class Solution {
public:vector<vector<int>>midRes,res;vector<int>mid;void backtrace(vector<int>&nums,int start){if(mid.size()>=2 ){//条件限制midRes.push_back(mid);}if(start==nums.size())//终止条件return;unordered_set<int> vistedSet;for(int i=start;i<nums.size();i++){if(vistedSet.find(nums[i])!=vistedSet.end())//去重continue;if(!mid.empty() && mid.back()>nums[i])//递增条件continue;//judge[nums[i]]=true;vistedSet.insert(nums[i]);//遍历标记mid.push_back(nums[i]);backtrace(nums,i+1);mid.pop_back();//回溯}}vector<vector<int>> findSubsequences(vector<int>& nums) {backtrace(nums,0);return midRes;}
};
46.全排列
思路:跟子集的代码几乎一样,主要区别在于
class Solution {
public:vector<vector<int>>res;vector<int>mid;void backtrace(vector<int>&nums,int start){if(start==nums.size()){res.push_back(mid);}for(int i=0;i<nums.size();i++){if(find(mid.begin(),mid.end(),nums[i])!=mid.end())//树枝去重continue;mid.push_back(nums[i]);backtrace(nums,start+1);mid.pop_back();}}//树枝去重vector<vector<int>> permute(vector<int>& nums) {backtrace(nums,0);return res;}
};
47.全排列||
思路一:使用哈希表进行树枝下标去重(因为有重复元素)
问题:在数组去重时时间复杂度过高
class Solution {
public:vector<vector<int>>res;vector<int>mid;unordered_map<int,bool>map;void backtrace(vector<int>&nums,int start){if(start==nums.size()){if(find(res.begin(),res.end(),mid)==res.end())//数组去重res.push_back(mid);return;}for(int i=0;i<nums.size();i++){if(map[i])//树枝去重continue;mid.push_back(nums[i]);map[i]=true;backtrace(nums,start+1);mid.pop_back();map[i]=false;}}vector<vector<int>> permuteUnique(vector<int>& nums) {//sort(nums.begin(),nums.end());backtrace(nums,0);return res;}
};
323.重新安排行程
思路:首先记录航班的映射关系,然后从起点开始根据映射关系一一添加(横向遍历,纵向递归)
注意:
-
起点航班要先添加
-
如果添加的路线等于航班数+1时,说明已经走完全部航班(如五个航班,必然是六个站点)
-
递归深入的时候需要判断当前映射关系是否被添加过
class Solution {
public:unordered_map<string,map<string,int>>targets;vector<string>midres;bool backtrace(vector<vector<string>>& tickets){if(midres.size()==tickets.size()+1)//航班已经走完的终止条件return true;for(pair<const string,int>&target:targets[midres[midres.size()-1]]){//遍历映射关系if(target.second>0){//当映射关系还存在时midres.push_back(target.first);target.second--;if(backtrace(tickets)) return true;//已经找到一条路线midres.pop_back();target.second++;}}return false;}vector<string> findItinerary(vector<vector<string>>& tickets) {midres.push_back("JFK");//先添加起点航班for(auto it:tickets)targets[it[0]][it[1]]++;//记录映射关系backtrace(tickets);return midres;}
};
51.N皇后
思路:二维数组,行递归,列遍历
在列放置皇后的时候,要进行有效判断
- 1.判断列方向上有没有放置过(行方向是递归遍历进行的,所以只可能放置一个)
- 2.判断左上方有没有放置过
- 3.判断右上方有没有放置过(左下方和右下方还没有遍历到,无需遍历)
class Solution {
public:vector<vector<string>>res;bool isvald(int row,int lie,vector<string>&mids,int n){//检查列for(int i=0;i<row;i++){if(mids[i][lie]=='Q')return false;}//检查左上方for(int i=row-1,j=lie-1;i>=0 && j>=0;i--,j--){if(mids[i][j]=='Q')return false;}//检查右上方for(int i=row-1,j=lie+1;i>=0 && j<n;i--,j++){if(mids[i][j]=='Q')return false;}return true;}void backtrace(vector<string>&mids,int n,int row){if(row==n){res.push_back(mids);return;}for(int i=0;i<n;i++){//列的遍历if(isvald(row,i,mids,n)){//判断该位置是否有效mids[row][i]='Q';backtrace(mids,n,row+1);//传入的是下一行不是下一列mids[row][i]='.';}}}vector<vector<string>> solveNQueens(int n) {vector<string>mids(n,string(n,'.'));//二维数组初始化backtrace(mids,n,0);return res;}
};
37.解数独
思路:二维遍历,递归判断
class Solution {
public:bool backtrace(vector<vector<char>>&board){for(int i=0;i<board.size();i++){//遍历行for(int j=0;j<board[0].size();j++){//遍历列if(board[i][j]=='.'){for(char k='1';k<='9';k++){if(isValid(i,j,k,board)){board[i][j]=k;if(backtrace(board)) return true;board[i][j]='.';}}return false;//9个数都遍历完都不对,说明这个位置无法插入}}}return true;//遍历完没有返回false,说明完全ok}bool isValid(int row,int col,char val,vector<vector<char>>&board){for(int i=0;i<9;i++){//判断行里是否重复if(board[row][i]==val) return false;}//判断列里是否重复for(int i=0;i<9;i++){if(board[i][col]==val) return false;}//判断九宫格里是否重复int startRow=(row/3)*3;//得到的是九宫格内的起始坐标int startCol=(col/3)*3;for(int i=startRow;i<startRow+3;i++){for(int j=startCol;j<startCol+3;j++){if(board[i][j]==val) return false;}}return true;}void solveSudoku(vector<vector<char>>& board) {backtrace(board);}
};