集合列表和数组
本文中介绍的概念为适用于所有编程语言的抽象理论,具体实现会由编程语言的不同而稍有差别。
具体介绍数组之前,我们先来了解一下集合、列表和数组的概念之间的差别。
集合
集合一般被定义为:由一个或多个确定的元素所构成的整体。
通俗来讲,集合就是将一组事物组合在一起。你可以将力扣的题库看作一个集合:

也可以将力扣商店里的礼品看作一个集合:
甚至可以将桌面上的物品当作一个集合。
集合有什么特性呢?
首先,集合里的元素类型不一定相同。 你可以将商品看作一个集合,也可以将整个商店看作一个集合,这个商店中有人或者其他物品也没有关系。
其次,集合里的元素没有顺序。 我们不会这样讲:我想要集合中的第三个元素,因为集合是没有顺序的。
事实上,这样的集合并不直接存在于编程语言中。然而,实际编程语言中的很多数据结构,就是在集合的基础上添加了一些规则形成的。
列表
列表(又称线性列表)的定义为:是一种数据项构成的有限序列,即按照一定的线性顺序,排列而成的数据项的集合。
列表的概念是在集合的特征上形成的,它具有顺序,且长度是可变的。你可以把它看作一张购物清单:

在这张清单中:
- 购物清单中的条目代表的类型可能不同,但是按照一定顺序进行了排列;
- 购物清单的长度是可变的,你可以向购物清单中增加、删除条目。
在编程语言中,列表最常见的表现形式有数组和链表,而我们熟悉的栈和队列则是两种特殊类型的列表。除此之外,向列表中添加、删除元素的具体实现方式会根据编程语言的不同而有所区分。
数组
数组是列表的实现方式之一,也是面试中经常涉及到的数据结构。
正如前面提到的,数组是列表的实现方式,它具有列表的特征,同时也具有自己的一些特征。然而,在具体的编程语言中,数组这个数据结构的实现方式具有一定差别。比如 C++ 和 Java 中,数组中的元素类型必须保持一致,而 Python 中则可以不同。Python 中的数组叫做 list,具有更多的高级功能。
那么如何从宏观上区分列表和数组呢?这里有一个重要的概念:索引。
首先,数组会用一些名为 索引 的数字来标识每项数据在数组中的位置,且在大多数编程语言中,索引是从 0 算起的。我们可以根据数组中的索引,快速访问数组中的元素。

而列表中没有索引,这是数组与列表最大的不同点。
其次,数组中的元素在内存中是连续存储的,且每个元素占用相同大小的内存。要理解这一点,我们需要了解数组在内存中的存储方式。
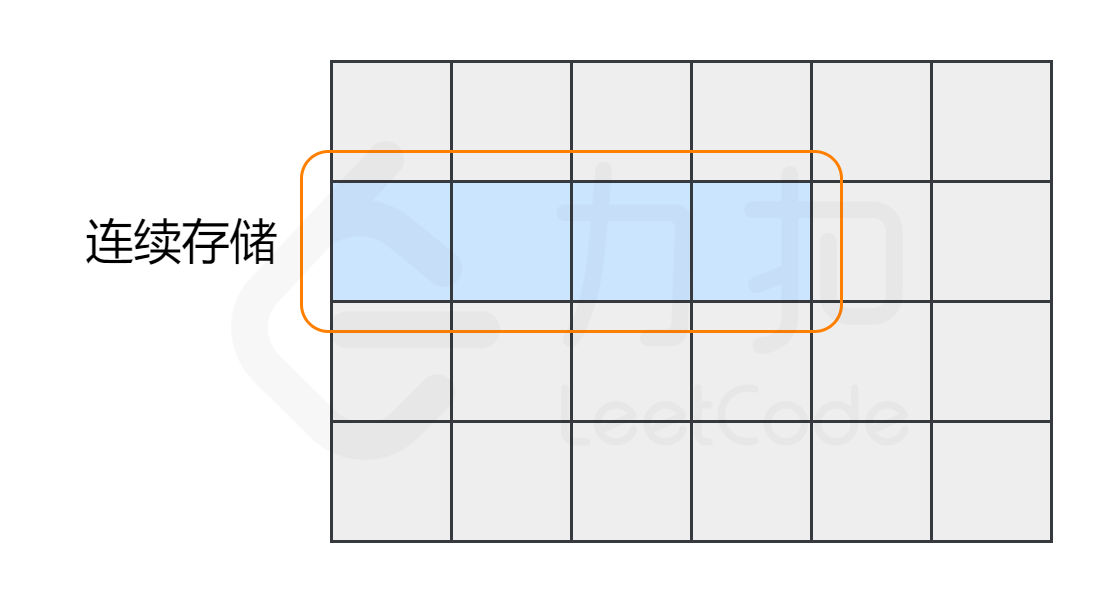
相反,列表中的元素在内存中可能彼此相邻,也可能不相邻。比如列表的另一种实现方式——链表,它的元素在内存中则不一定是连续的。
数组的操作
读取元素
读取数组中的元素,是通过访问索引的方式来读取的,索引一般从 0 开始。
在计算机中,内存可以看成一些已经排列好的格子,每个格子对应一个内存地址。一般情况下,数据会分散地存储在不同的格子中。
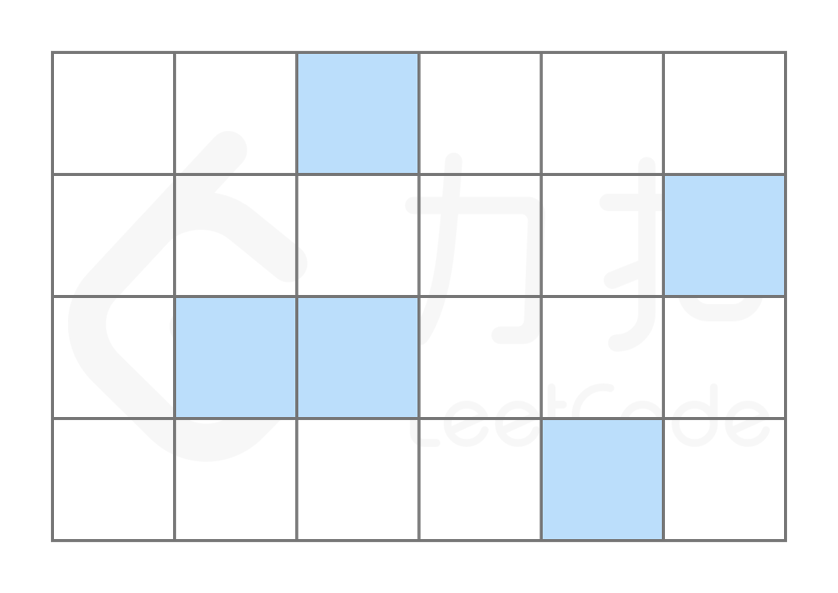
而对于数组,计算机会在内存中为其申请一段 连续 的空间,并且会记下索引为 0 处的内存地址。以数组 [“C”, “O”, “D”, “E”, “R”] 为例,它的各元素对应的索引及内存地址如下图所示。
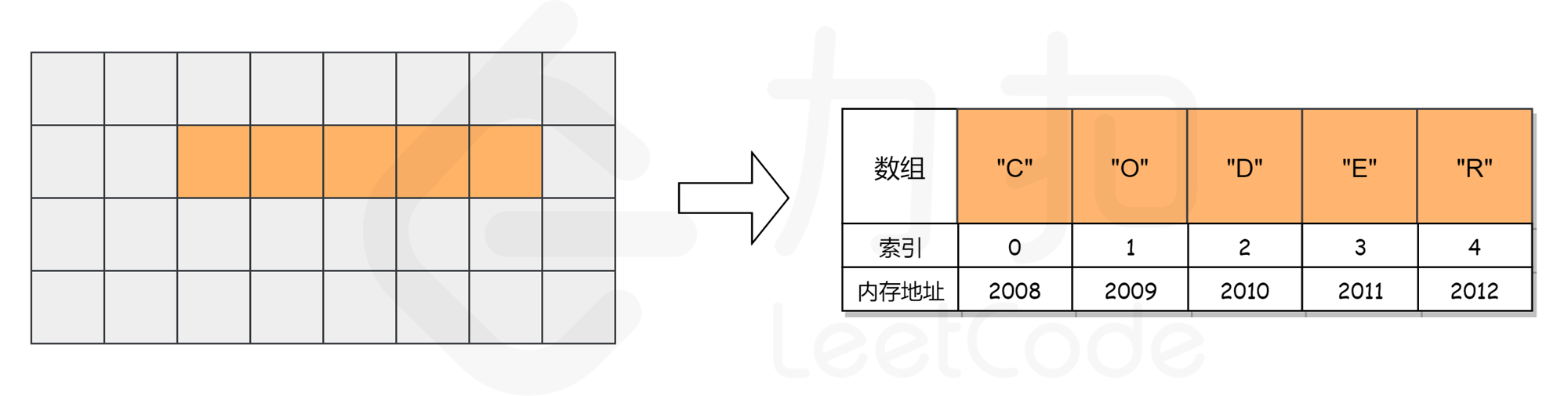
假如我们想要访问索引为 2 处的元素 “D” 时,计算机会进行以下计算:
- 找到该数组的索引 0 的内存地址: 2008;
- 将内存地址加上索引值,作为目标元素的地址,即 2008 + 2 = 2010,对应的元素为 “D”,这时便找到了目标元素。
我们知道,计算内存地址这个过程是很快的,而我们一旦知道了内存地址就可以立即访问到该元素,因此它的时间复杂度是常数级别。
查找元素
假如我们对数组中包含哪些元素并不了解,只是想知道其中是否含有元素 “E”,数组会如何查找元素 `“E” 呢?
与读取元素类似,由于我们只保存了索引为 0 处的内存地址,因此在查找元素时,只需从数组开头逐步向后查找就可以了。如果数组中的某个元素为目标元素,则停止查找;否则继续搜索直到到达数组的末尾。
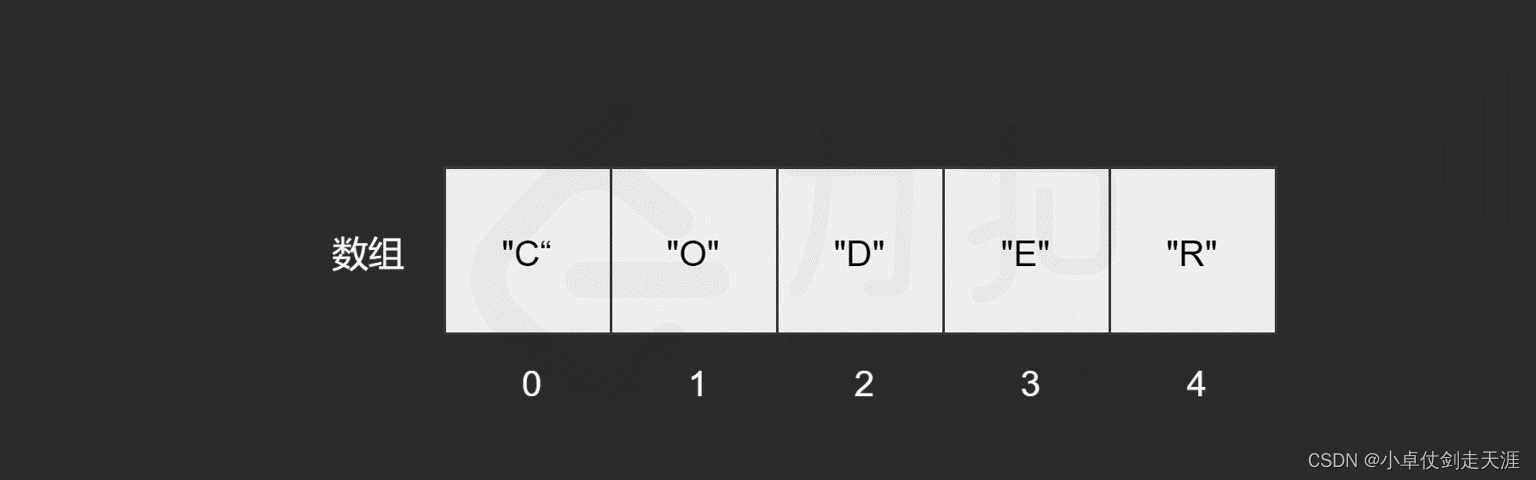
插入元素
我们发现,最坏情况下,搜索的元素为 “R”,或者数组中不包含目标元素时,我们需要查找 n 次,n 为数组的长度,因此查找元素的时间复杂度为 O(N),N。
假如我们想在原有的数组中再插入一个元素 “S” 呢?
如果要将该元素插入到数组的末尾,只需要一步。即计算机通过数组的长度和位置计算出即将插入元素的内存地址,然后将该元素插入到指定位置即可。
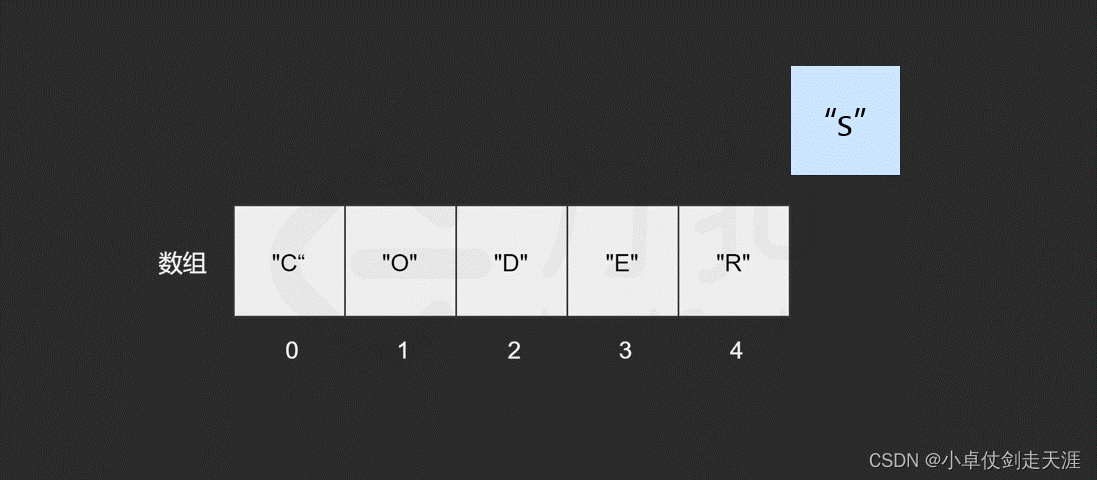
然而,如果要将该元素插入到数组中的其他位置,则会有所区别,这时我们首先需要为该元素所要插入的位置 腾出 空间,然后进行插入操作。比如,我们想要在索引 2 处插入 “S”。

我们发现,如果需要频繁地对数组元素进行插入操作,会造成时间的浪费。事实上,另一种数据结构,即链表可以有效解决这个问题,我们将在另外的卡片中进行学习。
删除元素
删除元素与插入元素的操作类似,当我们删除掉数组中的某个元素后,数组中会留下 空缺 的位置,而数组中的元素在内存中是连续的,这就使得后面的元素需对该位置进行 填补 操作。
以删除索引 1 中的元素 “O” 为例,具体过程如图所示。

原文链接:https://leetcode.cn/leetbook/read/array-and-string/yjcir/
来源:力扣(LeetCode)