1.前言
第一次接触动态规划,不知道具体什么意思,做了题才发现动态规划就是把大问题变成小问题,并解决了小问题重复计算的方法称为动态规划。比如上楼梯,一次上一阶或二阶,求有多少种算法,就可以拆成最后一阶的方法数等于前一阶的方法数加前两阶的方法数,这就是递归算法。但是这样往往会超出时间限制,因为里面有大量的重复,比如一共5阶,F(5)=F(4)+F(3),其中F(4)=F(3)+F(2),这里面F(3)就被重复计算了,这时我们需要将算好的值储存下来,避免重复计算,这就是记忆递归算法。
递归是一种程序的实现方式:函数的自我调用。
动态规划:是一种解决问 题的思想,大规模问题的结果,是由小规模问 题的结果运算得来的。动态规划可用递归来实现(Memorization Search)
使用场景
满足两个条件
-
满足以下条件之一
-
求最大/最小值(Maximum/Minimum )
-
求是否可行(Yes/No )
-
求可行个数(Count(*) )
-
-
满足不能排序或者交换(Can not sort / swap )
2.实战
2.1第70题
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?
心得:很经典的题目,用动态规划,之前一直有个疑问就是,递归的顺序是怎么执行的,是同时计算同一层的两个F(n-1)和F(n-2),还是先计算位于前面的F(n-1),直到算出F(n-1)再计算F(n-2),这次我直接打印出来了,发现是先递归计算出位于前面的F(n-1),这时该储存的已经储存好了,后面计算F(n-2)时就不会重复计算了。
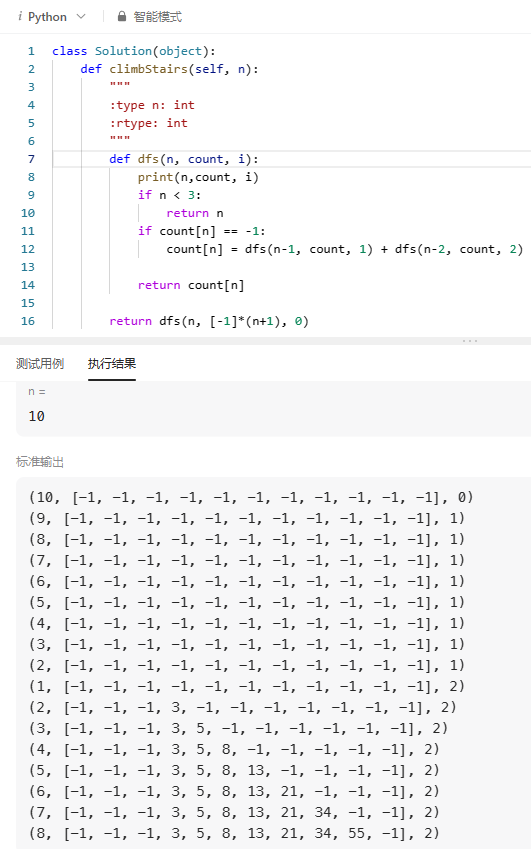

改成自下而上dp(动态规划)
class Solution(object):def climbStairs(self, n):""":type n: int:rtype: int"""if n==1:return 1elif n==2:return 2dp = [0]*(n+1)dp[1] = 1dp[2] = 2for i in range(3,n+1):dp[i] = dp[i-1] + dp[i-2]return dp[n]
因为该问题符合斐波那契数列,直接算
class Solution(object):def climbStairs(self, n):""":type n: int:rtype: int"""a = b = 1for i in range(2, n + 1):a, b = b, a + breturn b
2.2第118题
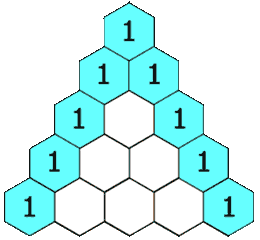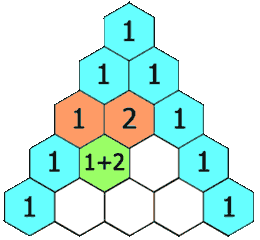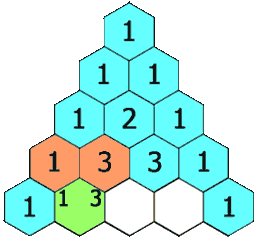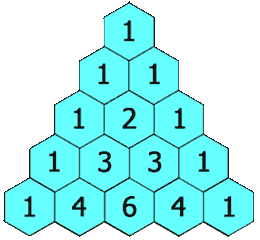
给定一个非负整数 numRows,生成「杨辉三角」的前 numRows 行。
在「杨辉三角」中,每个数是它左上方和右上方的数的和。
class Solution(object):def generate(self, numRows):""":type numRows: int:rtype: List[List[int]]"""if numRows==1:return [[1]]result = [[1]]for i in range(2,numRows+1):current = [1]*iif i>2:for j in range(1,i-1):current[j] = result[i-2][j-1]+result[i-2][j]result.append(current)return result
2.3第198题
你是一个专业的小偷,计划偷窃沿街的房屋。每间房内都藏有一定的现金,影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警。
给定一个代表每个房屋存放金额的非负整数数组,计算你 不触动警报装置的情况下 ,一夜之内能够偷窃到的最高金额。
心得:看到这种求最大金额的题目就要想到动态规划,动态规划就是要把大问题分为一个个的小问题来进行解决。这道题就是,可以把最高金额的问题分为求局部最高金额的问题,然后再递归就能解决了。感觉像是上楼梯的升级题目,多了一个max判断。自左往右。也可以使用递归,自右往左。
class Solution(object):def rob(self, nums):""":type nums: List[int]:rtype: int"""if len(nums) == 1:return nums[0]elif len(nums) == 2:return max(nums[0], nums[1])dp = [0]*(len(nums)+1)dp[1] = nums[0]dp[2] = nums[1]for i in range(3,len(nums)+1):dp[i] = max(dp[i-3] + nums[i-1], dp[i-2] + nums[i-1])return max(dp[-1], dp[-2])
上述方法使用了数组存储结果。考虑到每间房屋的最高总金额只和该房屋的前两间房屋的最高总金额相关,因此可以使用滚动数组,在每个时刻只需要存储前两间房屋的最高总金额。
class Solution(object):def rob(self, nums):""":type nums: List[int]:rtype: int"""if len(nums) == 1:return nums[0]elif len(nums) == 2:return max(nums[0], nums[1])dp = [0]*(len(nums)+1)left = nums[0]right = max(nums[0], nums[1])for i in range(3,len(nums)+1):left, right = right, max(left + nums[i-1], right)return right
2.4第279题
完全背包问题
把题目翻译一下:完全平方数就是物品(可以无限件使用),凑个正整数n就是背包,问凑满这个背包最少有多少物品?
动规五部曲分析如下:
- 确定dp数组(dp table)以及下标的含义,dp[j]:和为j的完全平方数的最少数量为dp[j]
- 确定递推公式,dp[j] 可以由dp[j - i * i]推出, dp[j - i * i] + 1 便可以凑成dp[j]。此时我们要选择最小的dp[j],所以递推公式:dp[j] = min(dp[j - i * i] + 1, dp[j]);
- dp数组如何初始化,dp[0]表示 和为0的完全平方数的最小数量,那么dp[0]一定是0。有同学问题,那0 * 0 也算是一种啊,为啥dp[0] 就是 0呢?看题目描述,找到若干个完全平方数(比如 1, 4, 9, 16, ...),题目描述中可没说要从0开始,dp[0]=0完全是为了递推公式。非0下标的dp[j]应该是多少呢?从递归公式dp[j] = min(dp[j - i * i] + 1, dp[j]);中可以看出每次dp[j]都要选最小的,所以非0下标的dp[j]一定要初始为最大值,这样dp[j]在递推的时候才不会被初始值覆盖。
- 确定遍历顺序,我们知道这是完全背包,如果求组合数就是外层for循环遍历物品,内层for遍历背包。如果求排列数就是外层for遍历背包,内层for循环遍历物品。
- 举例推导dp数组
所以本题外层for遍历背包,内层for遍历物品,还是外层for遍历物品,内层for遍历背包,都是可以的!
我这里先给出外层遍历背包,内层遍历物品的代码:
class Solution(object):def numSquares(self, n):""":type n: int:rtype: int"""dp = [10]*(n+1)dp[0] = 0for i in range(n+1):j = 1while j*j <= i:dp[i] = min(dp[i-j*j]+1, dp[i])j = j + 1return dp[n]
外层遍历物品,内层遍历背包的代码:
因为是完全背包,所以外层的物品可以有很多个,内层就可以一直装。
class Solution(object):def numSquares(self, n):""":type n: int:rtype: int"""dp = [10]*(n+1)dp[0] = 0i = 1while i * i <= n:j = i * iwhile j <= n:dp[j] = min(dp[j-i*i]+1, dp[j])j = j + 1i = i + 1return dp[n]
2.5第322题
给你一个整数数组 coins ,表示不同面额的硬币;以及一个整数 amount ,表示总金额。
计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额,返回 -1 。
你可以认为每种硬币的数量是无限的。
心得:又是完全背包的题,按照上面的动规五部曲,
- 确定dp[j]的含义,dp[j]是当背包容量(也就是amount)为j时,最少的硬币个数。
- 递归公式为dp[j]=min(dp[j-coin]+1, dp[j])
- 初始化,当总金额为0时,需要的硬币个数为0,所以dp[0]=0。又因为求最小,所以初始化dp中都存入最大值float('inf')。
- 确定遍历顺序,组合就外面物品,里面背包。
- 举例推导dp数组。比如dp[5]。
class Solution(object):def coinChange(self, coins, amount):""":type coins: List[int]:type amount: int:rtype: int"""if amount==0:return 0dp = [float('inf')]*(amount+1)dp[0] = 0# 完全背包# 组合,外层物品,内层背包for i in range(len(coins)):coin = coins[i]j = coinwhile j <= amount:dp[j] = min(dp[j-coin]+1, dp[j])j = j + 1if dp[amount]==float('inf'):return -1else:return dp[amount]