队列是一种先进先出(FIFO)的数据结构,但有些情况下,操作的数据可能带有优先级,一般出队
列在这种情况下,数据结构应该提供两个最基本的操作,一个是返回最高优先级对象,一个是添加新的对象。
这种数据结构就是优先级队列(Priority Queue)。时,可能需要优先级高的元素先出队列,该中场景下,使用队列显然不合适。
PriorityQueue底层使用了堆这种数据结构,而堆实际就是在完全二叉树的基础上进行了一些调整。
堆的概念
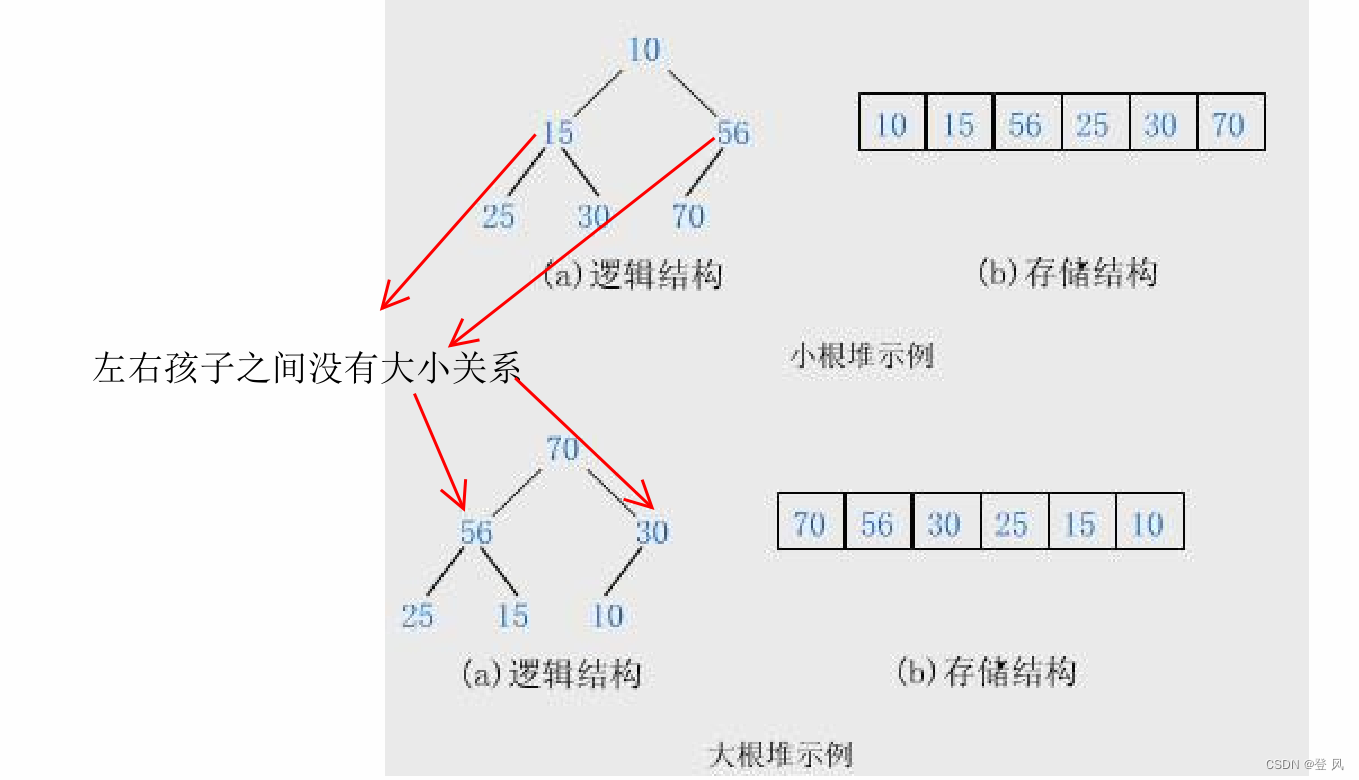
堆总是一棵完全二叉树。
堆中某个节点的值总是不大于或不小于其父节点的值;
将根节点最大的堆叫做最大堆或大根堆,根节点最小的堆叫做最小堆或小根堆。
****
堆的存储方式
可以层序的规则采用顺序的方式来高效存储
对于非完全二叉树,则不适合使用顺序方式进行存储,因为为了能够还原二叉树,空间中必须要存储空节点,就会导致空间利用率比较低。
假设i为节点在数组中的下标,
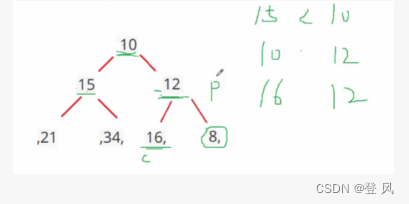
如果i为0,则i表示的节点为根节点,否则i节点的双亲节点为 (i - 1)/2
如果2 * i + 1 小于节点个数,则节点i的左孩子下标为2 * i + 1,否则没有左孩子
如果2 * i + 2 小于节点个数,则节点i的右孩子下标为2 * i + 2,否则没有右孩子
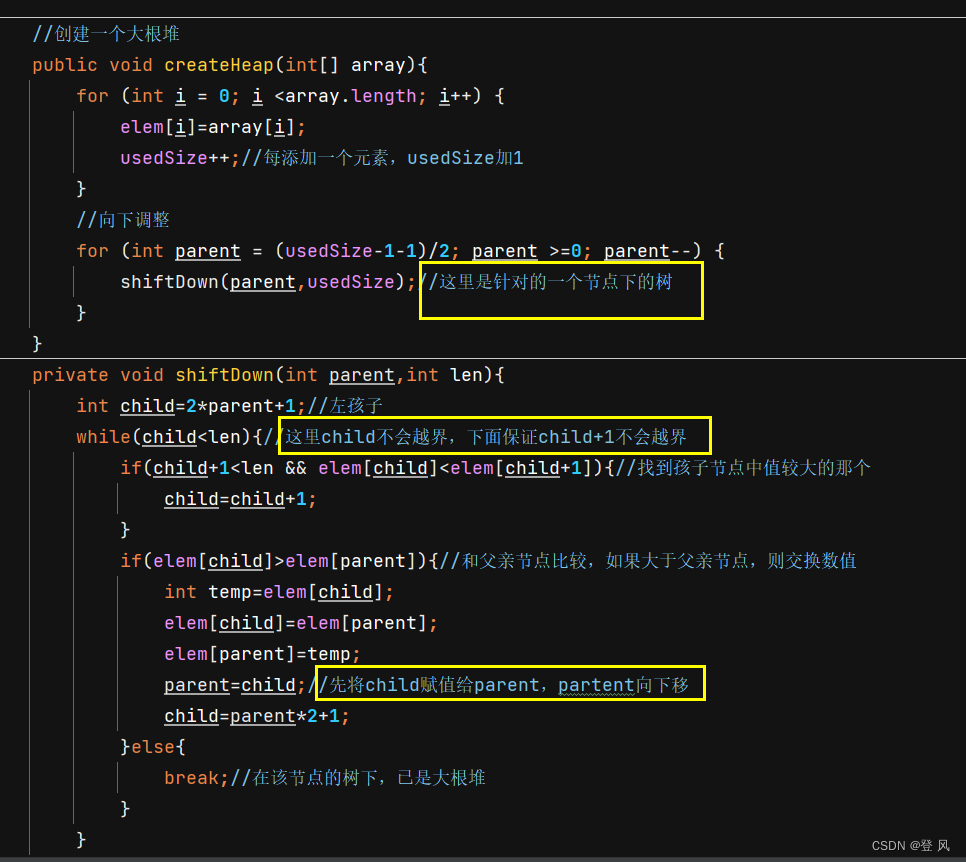
堆的创建
向下调整建堆
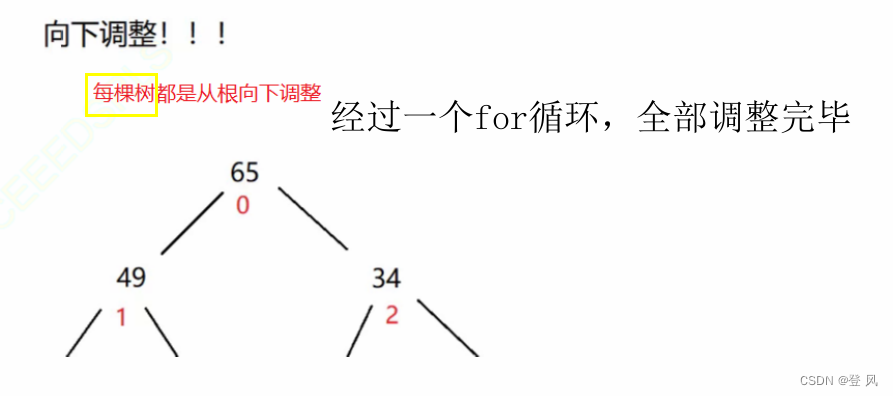
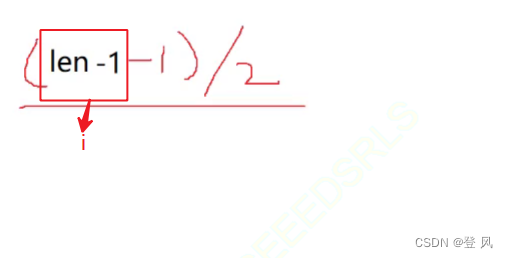
画图可以辅助理解
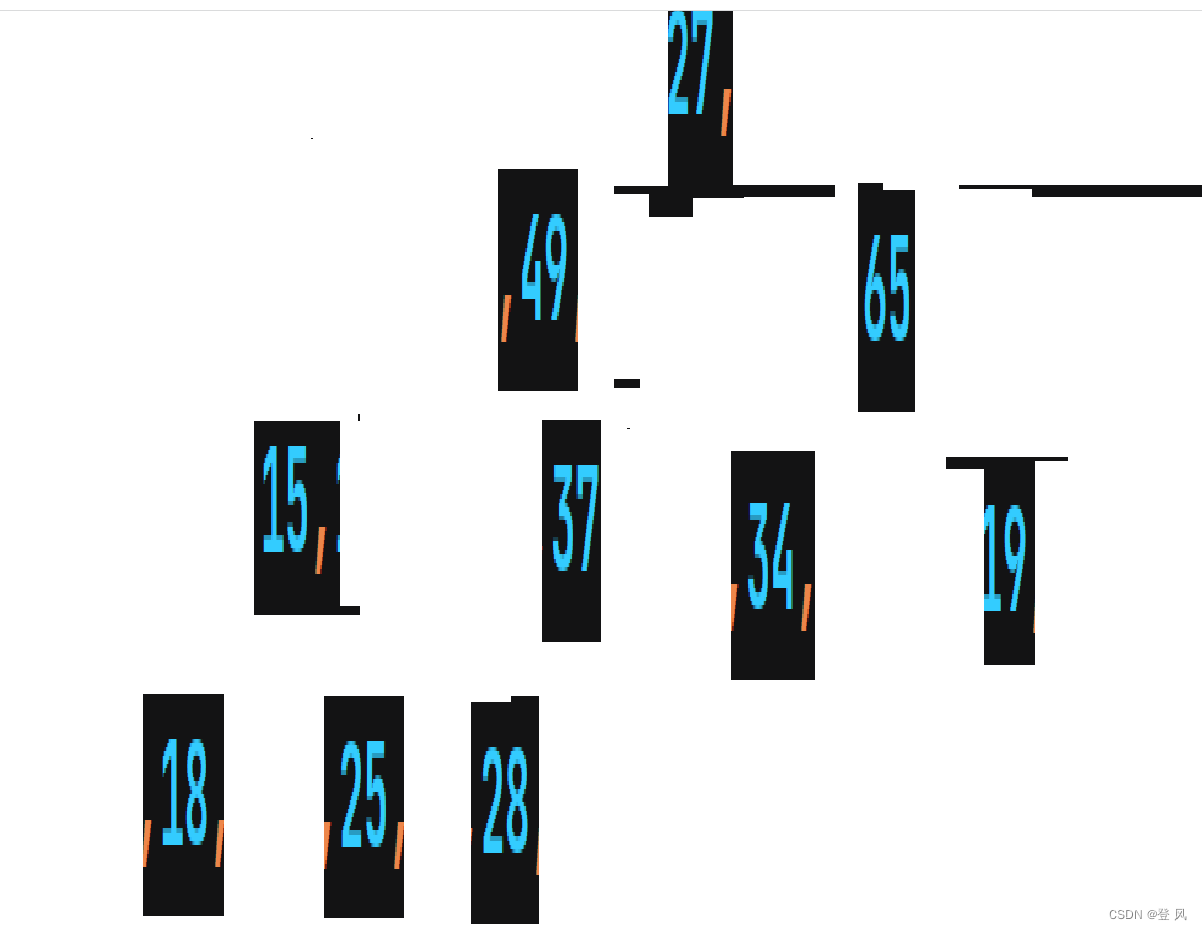
建堆的时间复杂度
满二叉树也是完全二叉树,此处为了简化使用满二叉树
向下调整 建堆的时间复杂度为O(N)。
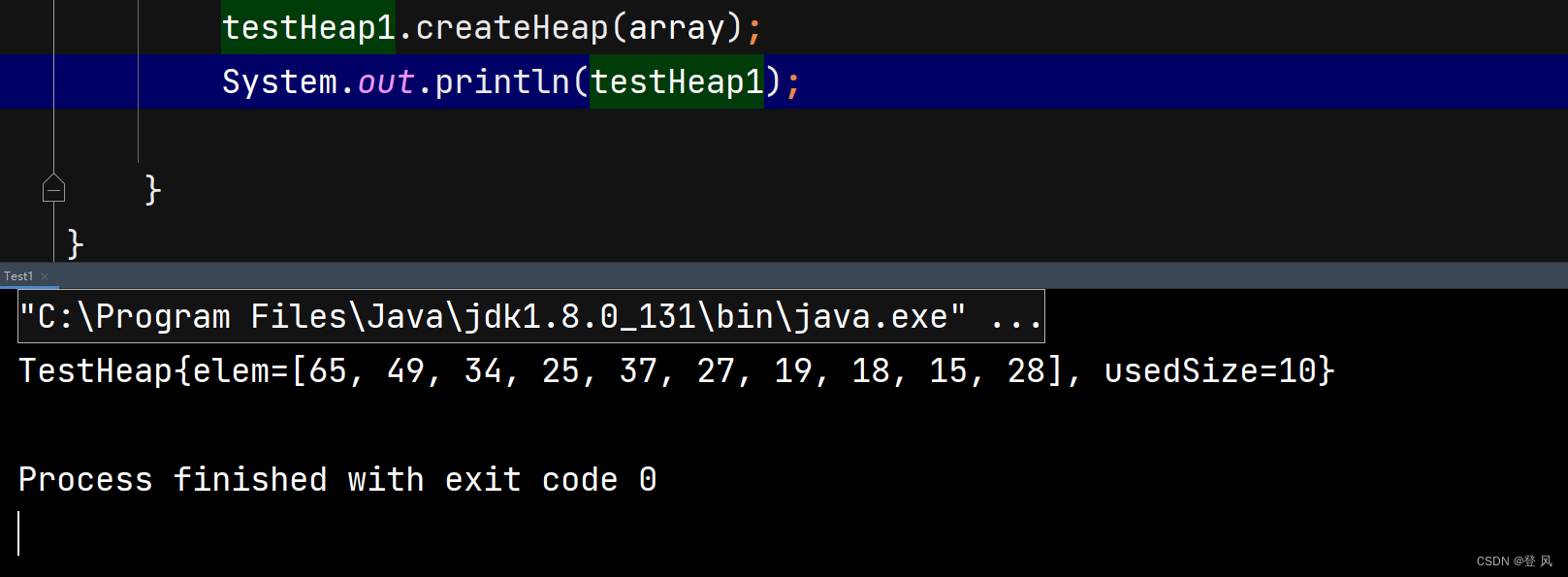
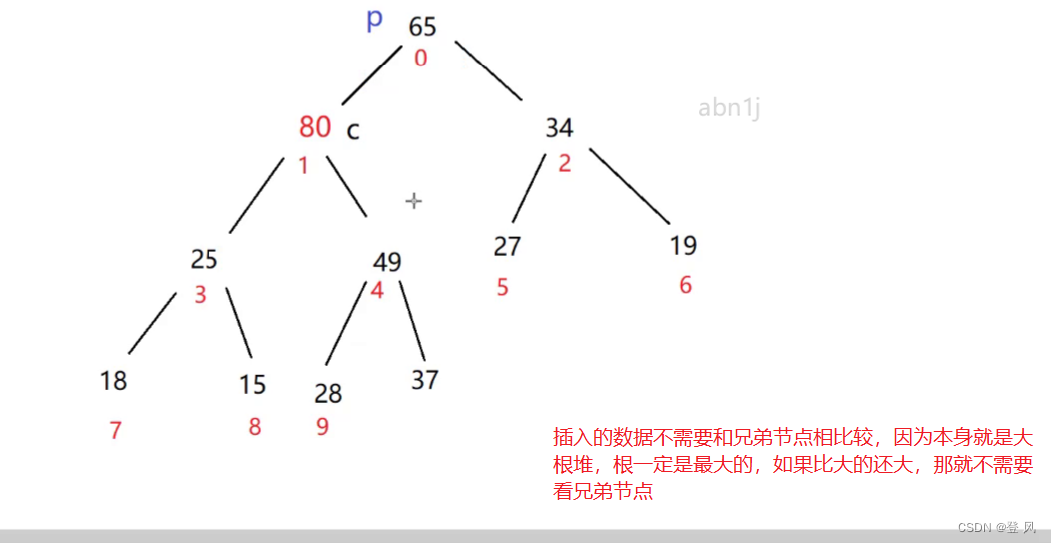
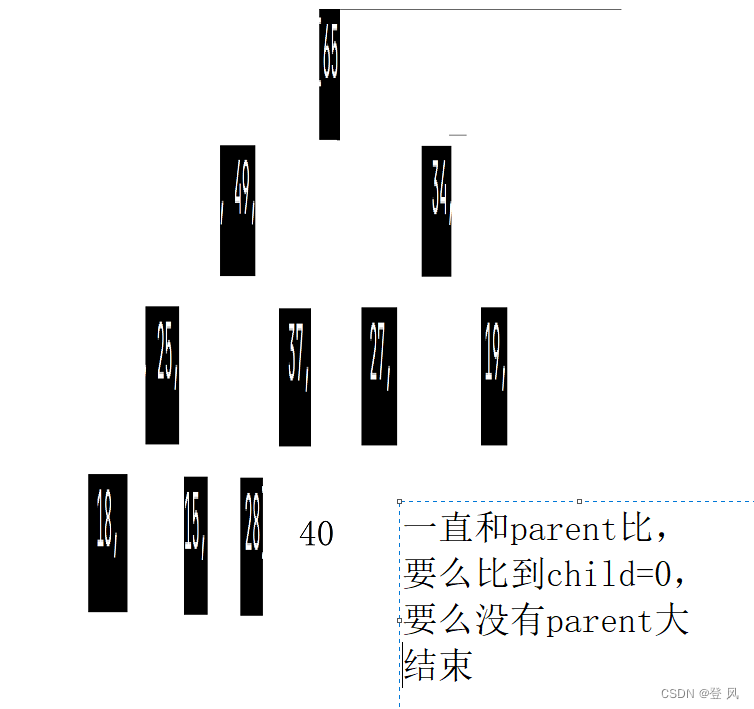
堆的插入与删除
堆的插入
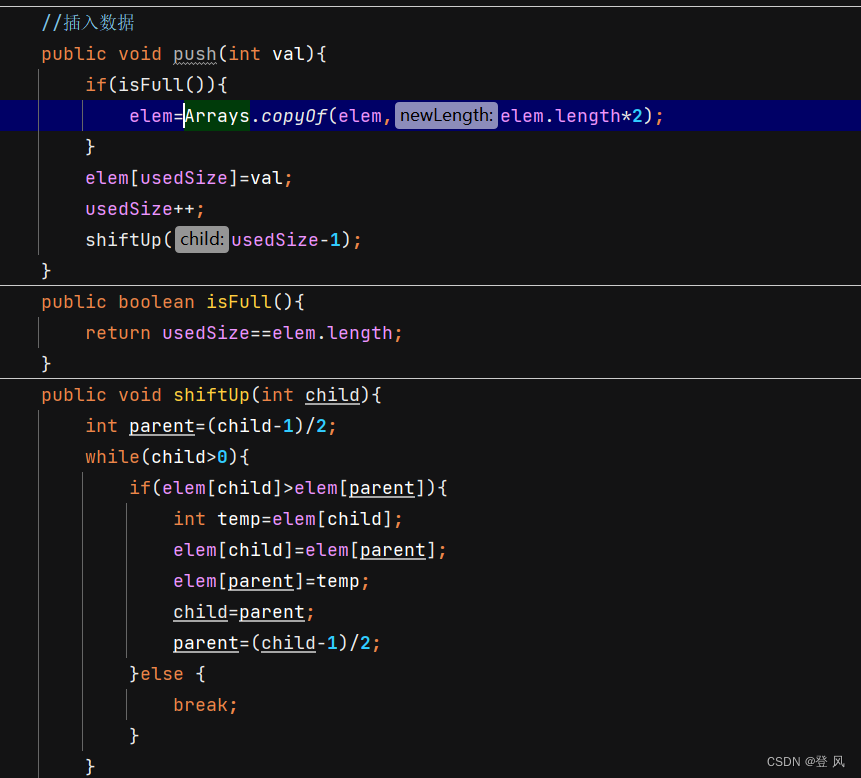
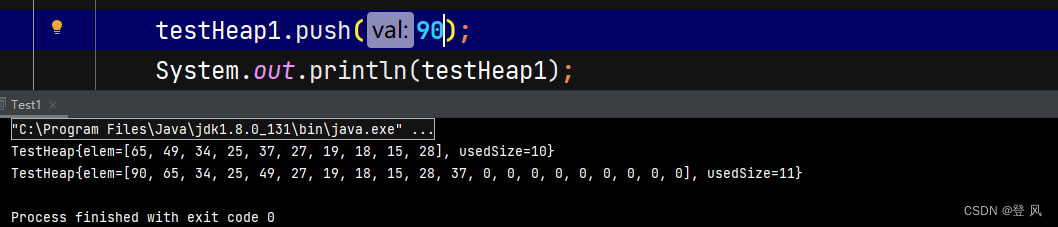
堆的插入总共需要两个步骤:
先将元素放入到底层空间中(注意:空间不够时需要扩容)
将最后新插入的节点向上调整,直到满足堆的性质
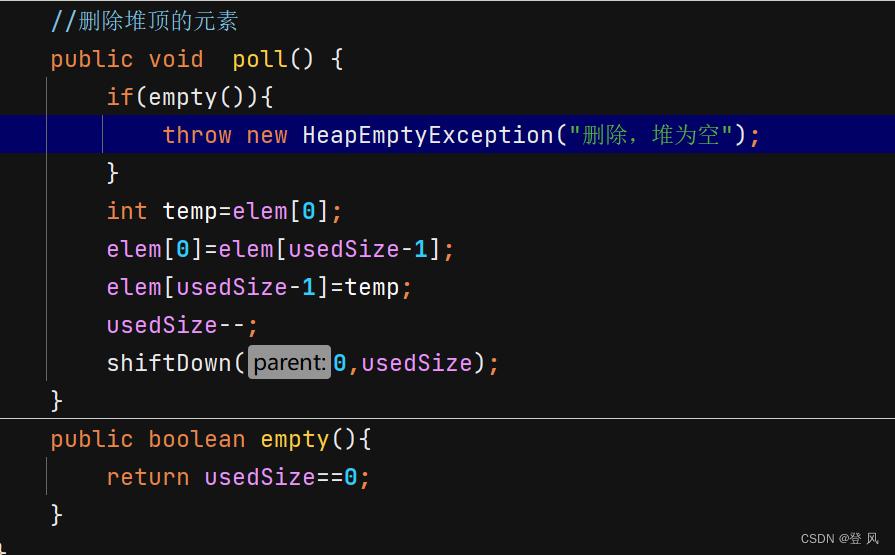
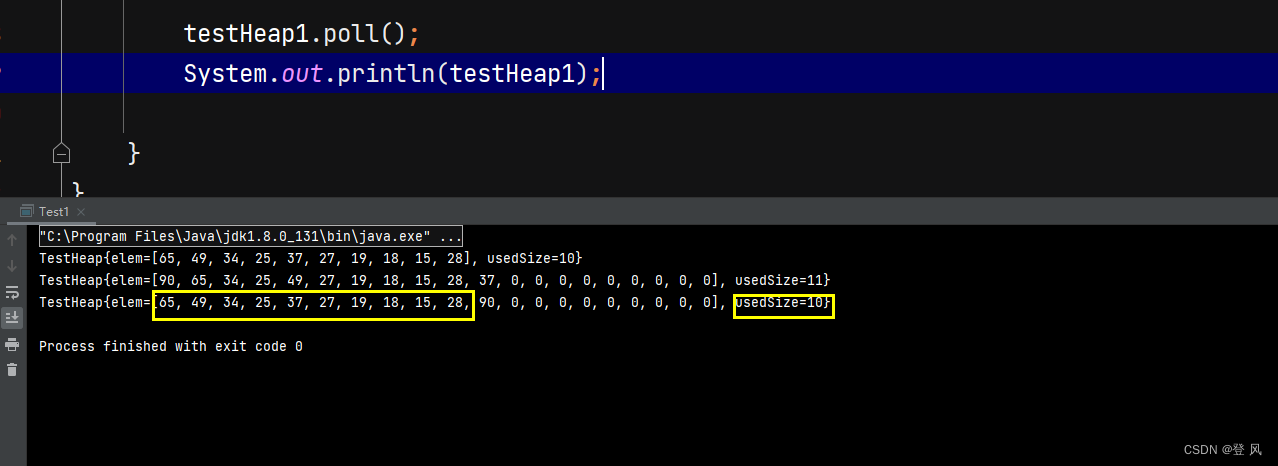
堆的删除
注意:堆的删除一定删除的是堆顶元素。具体如下:
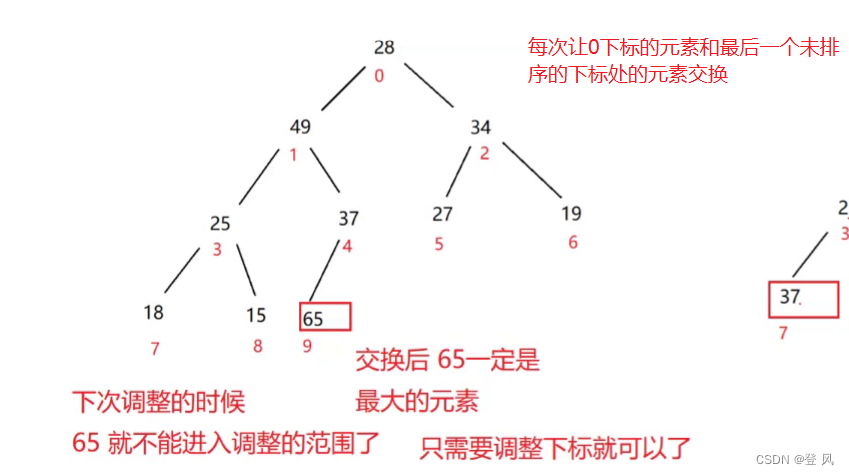
- 将堆顶元素和堆中最后一个元素交换
- 将堆中有效数据个数减少一个
- 对堆顶元素进行向下调整




PriorityQueue是线程不安全的,PriorityBlockingQueue是线程安全的
关于PriorityQueue的使用要注意:
使用时必须导入PriorityQueue所在的包
PriorityQueue中放置的元素必须要能够比较大小,不能插入无法比较大小的对象,否则会抛出ClassCastException异常
不能插入null对象,否则会抛出NullPointerException
默认情况下是小堆—即每次获取到的元素都是最小的元素
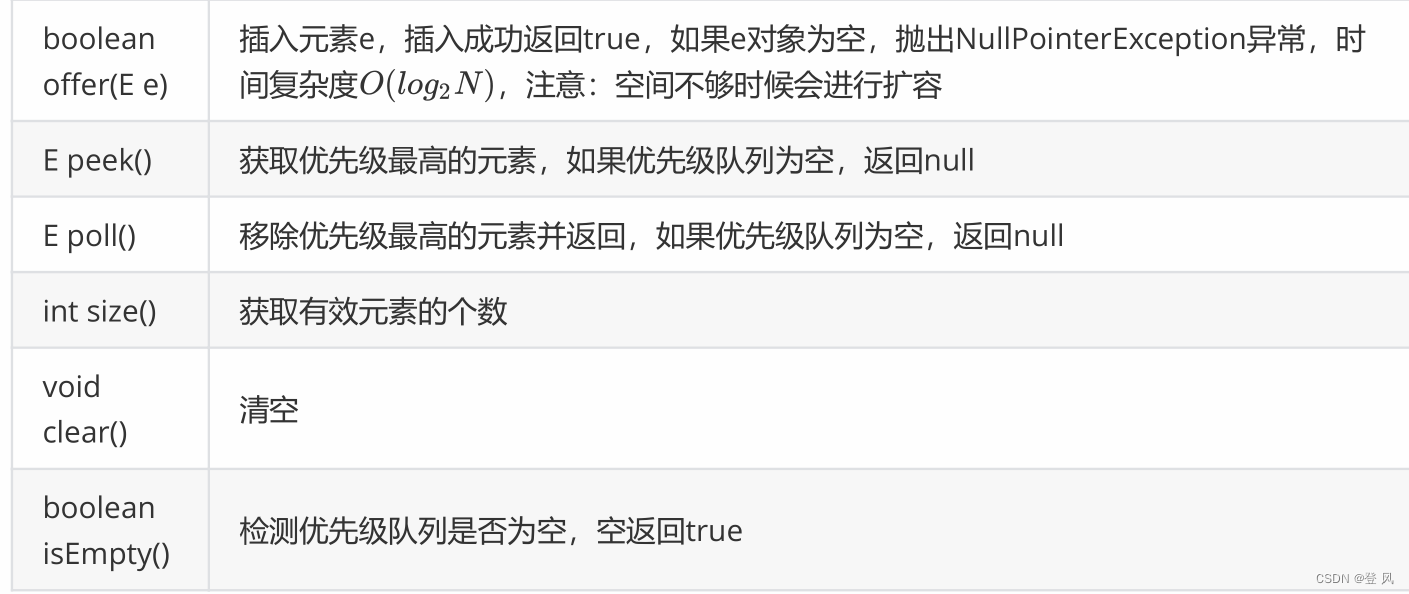
PriorityQueue常用接口

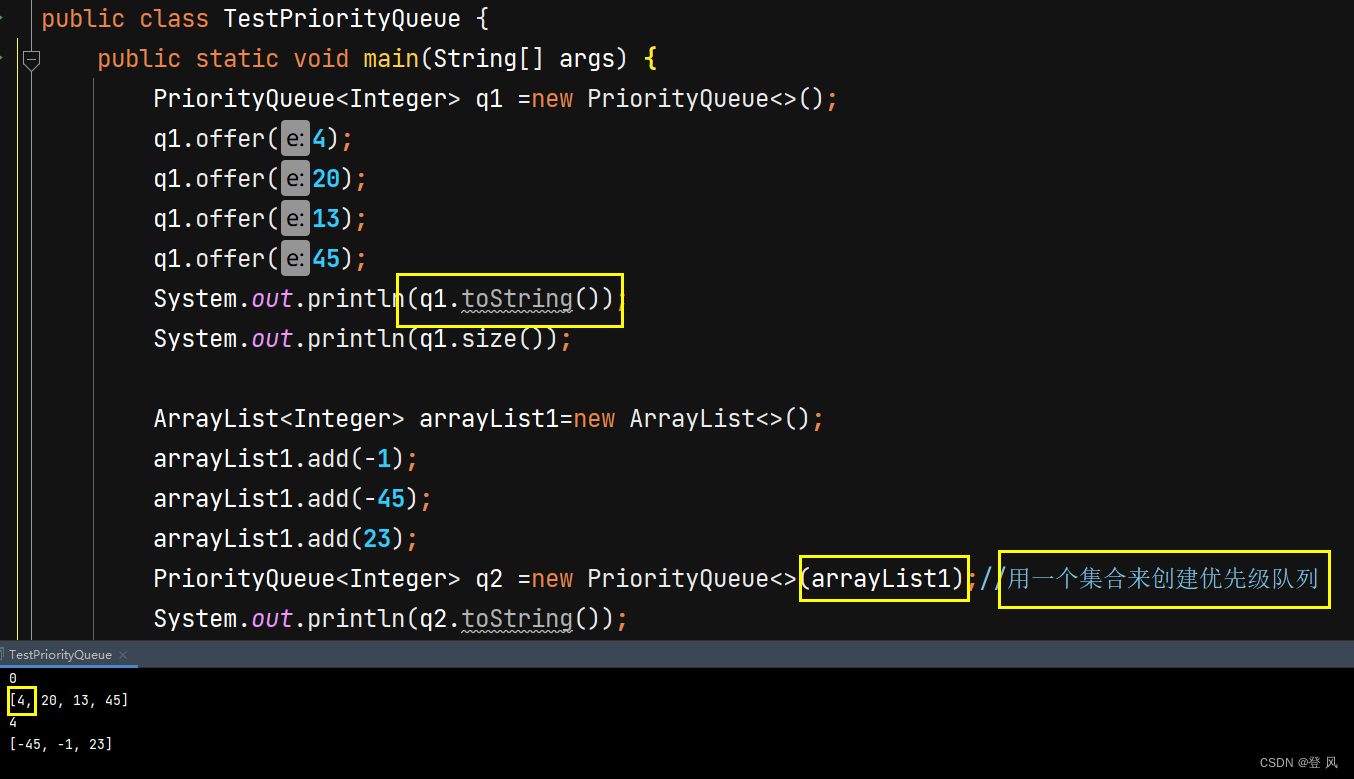
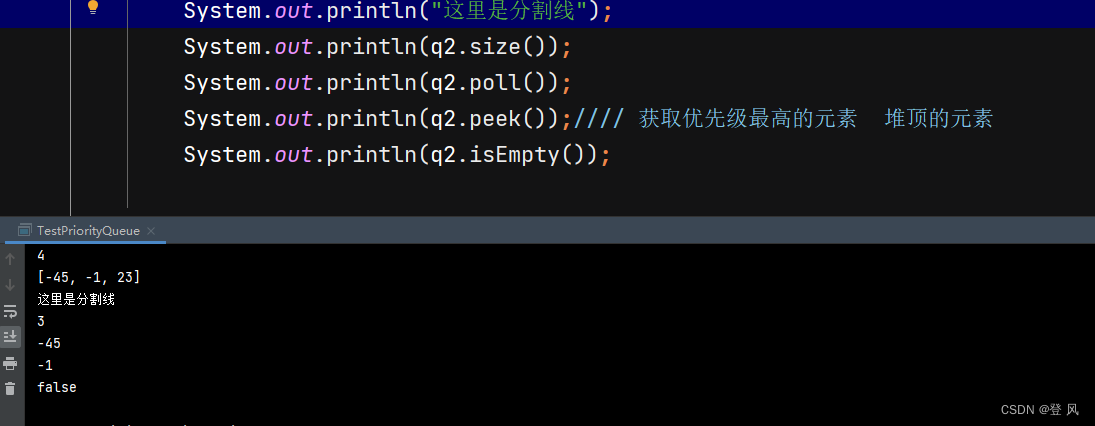

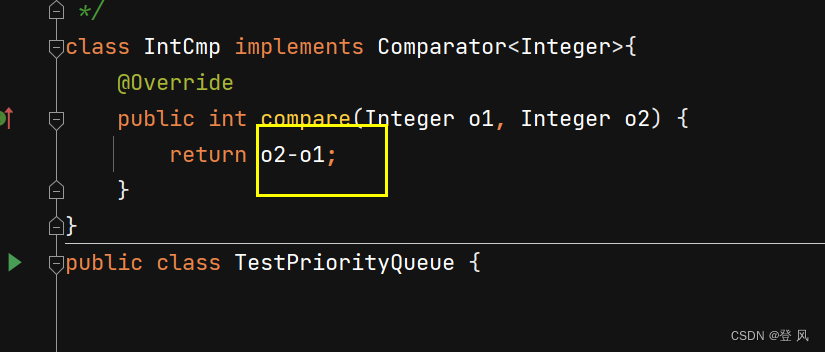
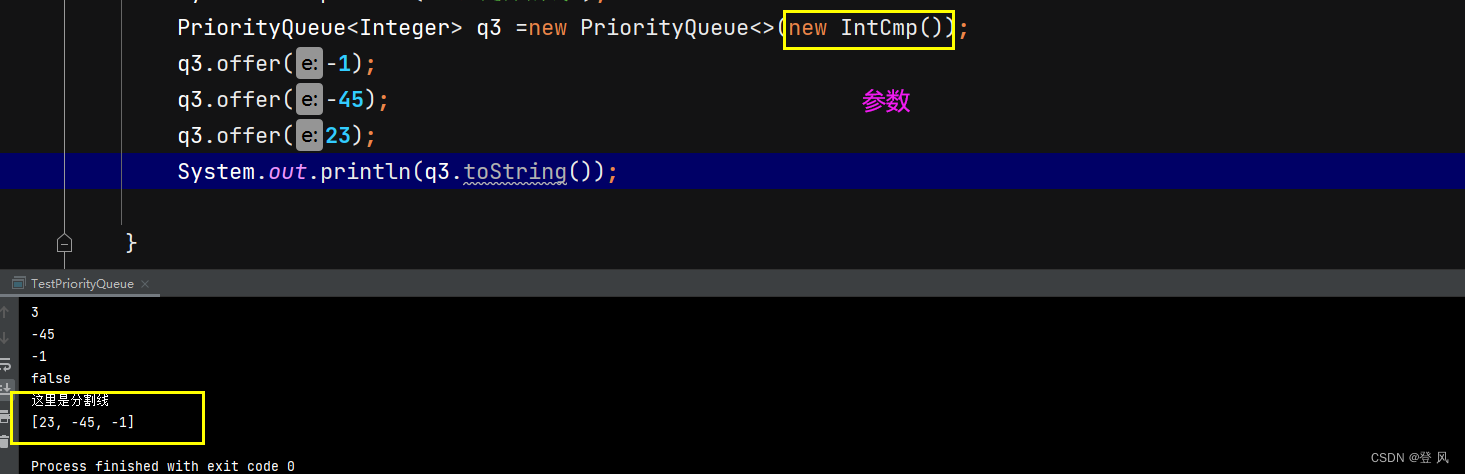
修改默认的小根堆为大根堆,这里我们直接实现Comparator接口,然后重写该接口中的compare方法
top-k问题:最大或者最小的前k个数据
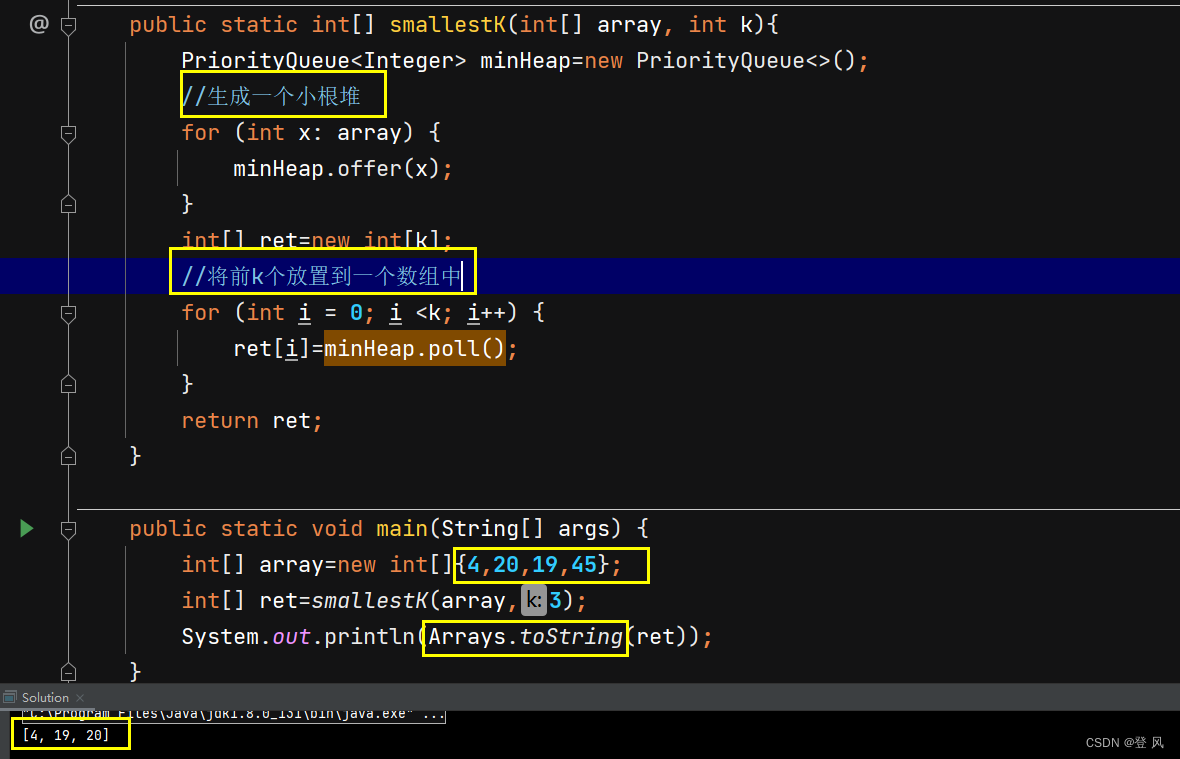
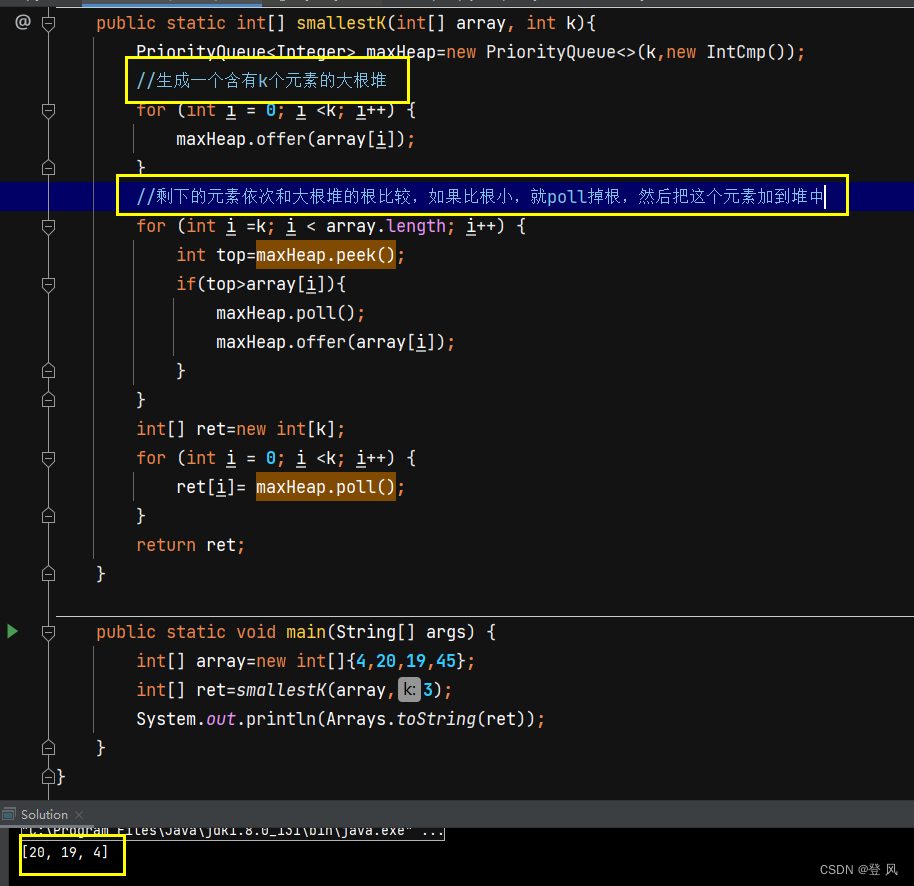
上述解法并不是最优解
下面这种解法

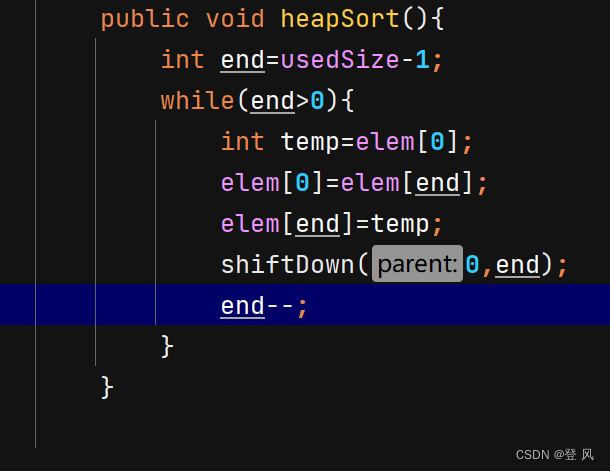
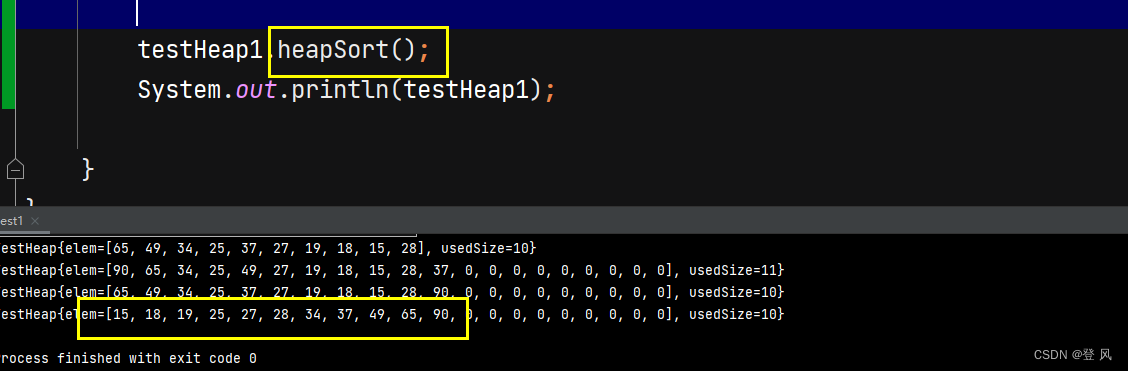
堆排序
堆排序即利用堆的思想来进行排序,总共分为两个步骤:
- 建堆
升序:建大堆
降序:建小堆 - 利用堆删除思想来进行排序