一、图像检索指标Rank1,map
参考:https://blog.csdn.net/weixin_41427758/article/details/81188164?spm=1001.2014.3001.5506
1.Rank1:
rank-k:算法返回的排序列表中,前k位为存在检索目标则称为rank-k命中。
常用的为rank1:首位为检索目标则rank-1命中。
2.map
mAP(mean average precision):反应检索的人在数据库中所有正确的图片排在排序列表前面的程度,能更加全面的衡量ReID算法的性能。如下图,该检索行人在gallery中有4张图片,在检索的list中位置分别为1、2、5、7,则ap为(1 / 1 + 2 / 2 + 3 / 5 + 4 / 7) / 4 =0.793;ap较大时,该行人的检索结果都相对靠前,对所有query的ap取平均值得到mAP

二、目标检测map
参考:目标检测mAP计算以及coco评价标准_哔哩哔哩_bilibili
目标检测中map的计算_map计算公式_RooKiChen的博客-CSDN博客
预测框先经过nms处理,然后计算TP,FP,FN。常见的map0.5,其中0.5是iou的阈值,与置信度无关。预测框与真实框的iou大于阈值为TP,小于阈值为FP。
- TP: IoU>thread的检测框数量(同一Ground Truth只计算一次)
- FP: IoU<=thread的检测框,或者是检测到同一个GT的多余检测框的数量
- FN: 没有检测到的GT的数量
对于要预测的样本,比如说有7个真实框需要预测,预测框 预测框与真实框的iou大于阈值记为True,小于阈值记为Fasle,将他们按照类别置信度排序,如下图,然后选不同大小的类别置信度作为分界线
1.类别置信度选0.98,如图,此时TP = 1,FP=0,FN=7-1=6
2.类别置信度选0.89,此时TP=2,FP=0,FN=7-2=5
........
分别得到若干个precision,recall,绘制PR曲线

对于同一Recall,不同的Precision,选最大的Precision,如下图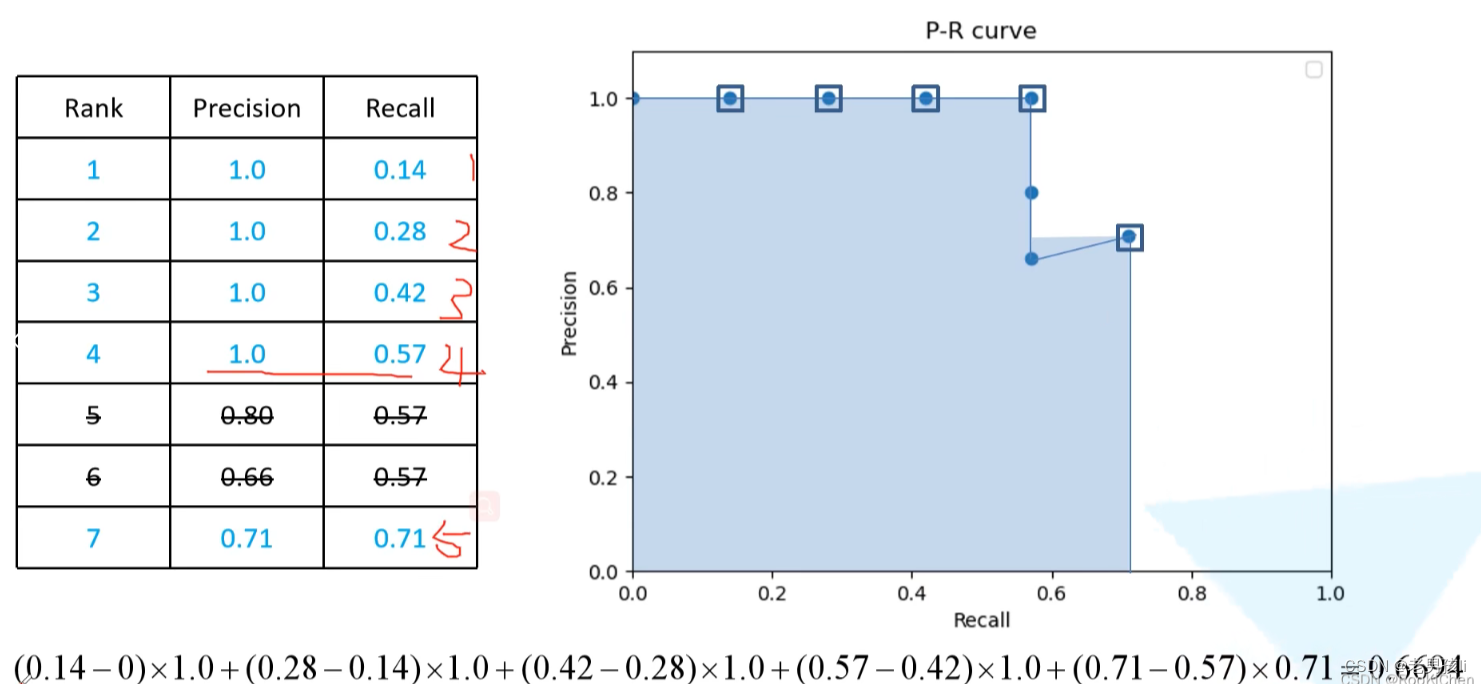











![成功解决SQL 错误 [22000]: 第3 行附近出现错误: 试图修改自增列[ID](达梦数据库)](https://img-blog.csdnimg.cn/5a35d69652eb41e8825ce00ce6df2765.png)