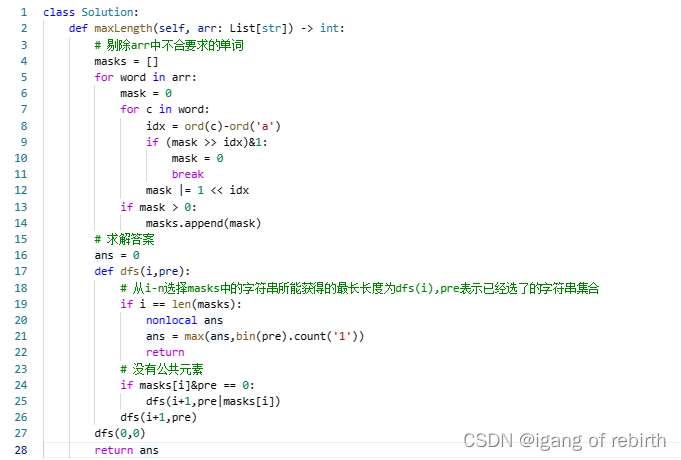
1239. 串联字符串的最大长度
核心思想:递归,选或者不选,定义dfs(i,pre)表示从i-n的满足要求的arr中选择字符串串联所能获得的最大长度为dfs(i,pre),pre表示已经选过的字符串所组成的集合。然后就有两种情况选,或者不选,选的话需要保证mask[i]和pre没有公共字母,dfs(i+1,pre|mask[i]),不选的话dfs(i+1,pre)。这里判断是否有公共字母利用了位运算,用二进制数来表示一个字符串,比如abc就等于111,c就等于100,然后1表示含这个字母,这里有一个误区就是arr不用处理,不容易想到,如果arr中的单词已经有相同字母了,那么我们就把它从arr中删除=不添加到masks,masks想到于剔除不满足要求的字符串后每个字符串的二进制数。统计答案的时候只需要把1的个数统计出来即可。
2826. 将三个组排序
核心思想:问题转换,问你nums的最长递增子序列是多长,然后用n-最长递增子序列即可,有点技巧性不太容易想到,这里求最长递增子序列我们用的是g[i]表示长度为i+1的递增子序列的最后一个元素的最小值为g[i],也可以用动态规划来求最长递增子序列。

2563. 统计公平数对的数目
核心思想:枚举,对于一个数对来说谁作为i,谁作为j都行,因为只要它们不是同一个数i<j的,所以我们可以对nums进行排序,这是这题的核心。然后对lower <= nums[i] + nums[j] <= upper进行变形,lower-nums[j] <= nums[i]<= upper-nums[j],我们通过枚举nums[j]然后看前面有多少个nums[i]满足这个范围要求即可,然后我们可以统计r:<= upper-nums[j]的个数,以及小于l:lower-nums[j]的个数,然后r-l就是满足要求的个数,由于nums是排好序的,所以统计个数可以用二分法来实现,这里就不再讨论二分的边界问题了。