文章目录

周赛360
- [2833. 距离原点最远的点](https://leetcode.cn/problems/furthest-point-from-origin/)
- - 脑经急转弯
- [2834. 找出美丽数组的最小和](https://leetcode.cn/problems/find-the-minimum-possible-sum-of-a-beautiful-array/)
- - 贪心
- [2835. 使子序列的和等于目标的最少操作次数](https://leetcode.cn/problems/minimum-operations-to-form-subsequence-with-target-sum/)
- - 贪心
- [2836. 在传球游戏中最大化函数值](https://leetcode.cn/problems/maximize-value-of-function-in-a-ball-passing-game/)
- - 树上倍增
  - [1483. 树节点的第 K 个祖先](https://leetcode.cn/problems/kth-ancestor-of-a-tree-node/)

周赛360

2833. 距离原点最远的点

简单

给你一个长度为 n 的字符串 moves ，该字符串仅由字符 'L'、'R' 和 '_' 组成。字符串表示你在一条原点为 0 的数轴上的若干次移动。

你的初始位置就在原点（0），第 i 次移动过程中，你可以根据对应字符选择移动方向：

如果 moves[i] = 'L' 或 moves[i] = '_' ，可以选择向左移动一个单位距离
如果 moves[i] = 'R' 或 moves[i] = '_' ，可以选择向右移动一个单位距离

移动 n 次之后，请你找出可以到达的距离原点最远的点，并返回 从原点到这一点的距离 。

示例 1：

输入：moves = "L_RL__R"
输出：3
解释：可以到达的距离原点 0 最远的点是 -3 ，移动的序列为 "LLRLLLR" 。

示例 2：

输入：moves = "_R__LL_"
输出：5
解释：可以到达的距离原点 0 最远的点是 -5 ，移动的序列为 "LRLLLLL" 。

示例 3：

输入：moves = "_______"
输出：7
解释：可以到达的距离原点 0 最远的点是 7 ，移动的序列为 "RRRRRRR" 。

提示：

1 <= moves.length == n <= 50
moves 仅由字符 'L'、'R' 和 '_' 组成

脑经急转弯

让_只往一个方向移动，移动的方向为R或L的方向

class Solution {public int furthestDistanceFromOrigin(String moves) {int cnt0 = 0, cntmove = 0;for(char c : moves.toCharArray()){if(c == '_') cnt0 += 1;else cntmove += (c == 'L' ? 1 : -1); }return Math.abs(cntmove) + cnt0;}
}

2834. 找出美丽数组的最小和

中等

给你两个正整数：n 和 target 。

如果数组 nums 满足下述条件，则称其为 美丽数组 。

nums.length == n.
nums 由两两互不相同的正整数组成。
在范围 [0, n-1] 内，不存在 两个不同下标 i 和 j ，使得 nums[i] + nums[j] == target 。

返回符合条件的美丽数组所可能具备的最小和。

示例 1：

输入：n = 2, target = 3
输出：4
解释：nums = [1,3] 是美丽数组。
- nums 的长度为 n = 2 。
- nums 由两两互不相同的正整数组成。
- 不存在两个不同下标 i 和 j ，使得 nums[i] + nums[j] == 3 。
可以证明 4 是符合条件的美丽数组所可能具备的最小和。

示例 2：

输入：n = 3, target = 3
输出：8
解释：
nums = [1,3,4] 是美丽数组。 
- nums 的长度为 n = 3 。 
- nums 由两两互不相同的正整数组成。 
- 不存在两个不同下标 i 和 j ，使得 nums[i] + nums[j] == 3 。
可以证明 8 是符合条件的美丽数组所可能具备的最小和。

示例 3：

输入：n = 1, target = 1
输出：1
解释：nums = [1] 是美丽数组。

提示：

1 <= n <= 105
1 <= target <= 105

贪心

class Solution {public long minimumPossibleSum(int n, int target) {int cnt = 0;long ans = 0l;while(cnt < target / 2 && cnt < n){ans += (cnt+1);cnt += 1;}int num = target;while(cnt < n){ans += num;num += 1;cnt += 1;}return ans;}
}

2835. 使子序列的和等于目标的最少操作次数

困难

给你一个下标从 0 开始的数组 nums ，它包含非负整数，且全部为 2 的幂，同时给你一个整数 target 。

一次操作中，你必须对数组做以下修改：

选择数组中一个元素 nums[i] ，满足 nums[i] > 1 。
将 nums[i] 从数组中删除。
在 nums 的末尾添加两个数，值都为 nums[i] / 2 。

你的目标是让 nums 的一个 子序列 的元素和等于 target ，请你返回达成这一目标的 最少操作次数 。如果无法得到这样的子序列，请你返回 -1 。

数组中一个 子序列 是通过删除原数组中一些元素，并且不改变剩余元素顺序得到的剩余数组。

示例 1：

输入：nums = [1,2,8], target = 7
输出：1
解释：第一次操作中，我们选择元素 nums[2] 。数组变为 nums = [1,2,4,4] 。
这时候，nums 包含子序列 [1,2,4] ，和为 7 。
无法通过更少的操作得到和为 7 的子序列。

示例 2：

输入：nums = [1,32,1,2], target = 12
输出：2
解释：第一次操作中，我们选择元素 nums[1] 。数组变为 nums = [1,1,2,16,16] 。
第二次操作中，我们选择元素 nums[3] 。数组变为 nums = [1,1,2,16,8,8] 。
这时候，nums 包含子序列 [1,1,2,8] ，和为 12 。
无法通过更少的操作得到和为 12 的子序列。

示例 3：

输入：nums = [1,32,1], target = 35
输出：-1
解释：无法得到和为 35 的子序列。

提示：

1 <= nums.length <= 1000
1 <= nums[i] <= 230
nums 只包含非负整数，且均为 2 的幂。
1 <= target < 231

贪心

https://leetcode.cn/problems/minimum-operations-to-form-subsequence-with-target-sum/solutions/2413344/tan-xin-by-endlesscheng-immn/

class Solution {// 无解的情况，sum(nums) < target// 用 二进制 思考， 从二进制位数从低到高思考// 如果 target 的第 i 位是0，跳过// 如果 target 的第 i 位是1//  先看nums中 <= 2^i 的元素和 s 能否 >= 2^i//  如果能，则一定可以凑出 2^i，无需操作，从s中减去 2^i//  如果不能，则需要把一个更大的数(设2^j)不断一分为二，直至分解出 2^i 为止//      需要操作 j - i 次//      操作之后，2^i,2^(i+1),2^(j-1)就不用考虑了，直接从j开始考虑public int minOperations(List<Integer> nums, int target) {long s = 0;long[] cnt = new long[31];for(int x : nums){s += x;//Integer.numberOfTrailingZeros()方法返回指定int值的二进制补码二进制表示形式中最低顺序（“最右”）一位之后的零位数目。cnt[Integer.numberOfTrailingZeros(x)]++;}if(s < target) return -1;s = 0;int ans = 0, i = 0;while((1L << i) <= target){s += cnt[i] << i;int mask = (int)((1L << ++i) - 1);if(s >= (target & mask))continue;ans++; // 一定要找更大的数操作for(; cnt[i] == 0; i++)ans++; // 还没找到，继续找更大的数}return ans;}
}

2836. 在传球游戏中最大化函数值

困难

给你一个长度为 n 下标从 0 开始的整数数组 receiver 和一个整数 k 。

总共有 n 名玩家，玩家编号互不相同，且为 [0, n - 1] 中的整数。这些玩家玩一个传球游戏，receiver[i] 表示编号为 i 的玩家会传球给编号为 receiver[i] 的玩家。玩家可以传球给自己，也就是说 receiver[i] 可能等于 i 。

你需要从 n 名玩家中选择一名玩家作为游戏开始时唯一手中有球的玩家，球会被传恰好 k 次。

如果选择编号为 x 的玩家作为开始玩家，定义函数 f(x) 表示从编号为 x 的玩家开始，k 次传球内所有接触过球玩家的编号之和，如果有玩家多次触球，则 累加多次 。换句话说， f(x) = x + receiver[x] + receiver[receiver[x]] + ... + receiver(k)[x] 。

你的任务时选择开始玩家 x ，目的是 最大化 f(x) 。

请你返回函数的 最大值 。

注意：receiver 可能含有重复元素。

示例 1：

传递次数	传球者编号	接球者编号	x + 所有接球者编号
			2
1	2	1	3
2	1	0	3
3	0	2	5
4	2	1	6

输入：receiver = [2,0,1], k = 4
输出：6
解释：上表展示了从编号为 x = 2 开始的游戏过程。
从表中可知，f(2) 等于 6 。
6 是能得到最大的函数值。
所以输出为 6 。

示例 2：

传递次数	传球者编号	接球者编号	x + 所有接球者编号
			4
1	4	3	7
2	3	2	9
3	2	1	10

输入：receiver = [1,1,1,2,3], k = 3
输出：10
解释：上表展示了从编号为 x = 4 开始的游戏过程。
从表中可知，f(4) 等于 10 。
10 是能得到最大的函数值。
所以输出为 10 。

提示：

1 <= receiver.length == n <= 105
0 <= receiver[i] <= n - 1
1 <= k <= 1010

树上倍增

https://leetcode.cn/problems/maximize-value-of-function-in-a-ball-passing-game/solutions/2413298/shu-shang-bei-zeng-by-endlesscheng-xvsv/

class Solution {// 树上倍增, 记录// 1. 每个点，顺着 receiver 走 2^i 步之后的结点// 2. 从 x 的父节点，到走 2^i 后的节点 【路径上的节点编号之和】 - 倍增public long getMaxFunctionValue(List<Integer> receiver, long k) {int n = receiver.size();int m = 64 - Long.numberOfLeadingZeros(k); // k 的二进制长度// pa[x][i] 表示 节点x 顺着 receiver 走 2^i 步之后的结点为 pa[x][i]int[][] pa = new int[n][m];// sum[x][i] 表示 节点x 顺着 receiver 走 2^i 步之后 【路径上的节点编号之和】 long[][] sum = new long[n][m];for(int i = 0; i < n; i++){pa[i][0] = receiver.get(i);sum[i][0] = receiver.get(i);}for(int i = 0; i < m-1; i++){for(int x = 0; x < n; x++){int p = pa[x][i];pa[x][i+1] = pa[p][i];// 合并结点值之和// x-> a -> b -> y == (x -> a) + (b -> y) == sum[x][2] = sum[x][1] + sum[i][1]sum[x][i+1] = sum[x][i] + sum[p][i]; }}long ans = 0;// 枚举每一个点作为路径起点for(int i = 0; i < n; i++){long s = i; // 路径之和int x = i;// 枚举每一个比特位for(int j = 0; j < m; j++){if(((k >> j) & 1) == 1){ // k 的二进制从低到高第 i 位是 1s += sum[x][j]; x = pa[x][j]; // x向上跳 2^i 个节点}}ans = Math.max(ans, s);}return ans;}
}

1483. 树节点的第 K 个祖先

难度困难134

给你一棵树，树上有 n 个节点，按从 0 到 n-1 编号。树以父节点数组的形式给出，其中 parent[i] 是节点 i 的父节点。树的根节点是编号为 0 的节点。

树节点的第 k 个祖先节点是从该节点到根节点路径上的第 k 个节点。

实现 TreeAncestor 类：

TreeAncestor（int n， int[] parent） 对树和父数组中的节点数初始化对象。
getKthAncestor``(int node, int k) 返回节点 node 的第 k 个祖先节点。如果不存在这样的祖先节点，返回 -1 。

示例 1：

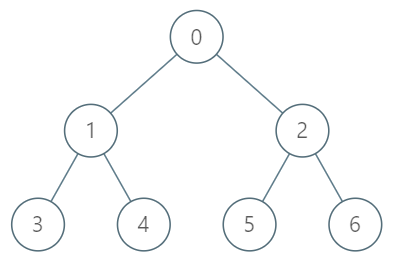
输入：
["TreeAncestor","getKthAncestor","getKthAncestor","getKthAncestor"]
[[7,[-1,0,0,1,1,2,2]],[3,1],[5,2],[6,3]]输出：
[null,1,0,-1]解释：
TreeAncestor treeAncestor = new TreeAncestor(7, [-1, 0, 0, 1, 1, 2, 2]);treeAncestor.getKthAncestor(3, 1);  // 返回 1 ，它是 3 的父节点
treeAncestor.getKthAncestor(5, 2);  // 返回 0 ，它是 5 的祖父节点
treeAncestor.getKthAncestor(6, 3);  // 返回 -1 因为不存在满足要求的祖先节点

提示：

1 <= k <= n <= 5 * 104
parent[0] == -1 表示编号为 0 的节点是根节点。
对于所有的 0 < i < n ，0 <= parent[i] < n 总成立
0 <= node < n
至多查询 5 * 104 次

树上倍增算法

https://leetcode.cn/problems/kth-ancestor-of-a-tree-node/solution/mo-ban-jiang-jie-shu-shang-bei-zeng-suan-v3rw/

预处理出每个节点的第 2^i个祖先节点，即第 2,4,8.... 个祖先节点(注意 x 的第1 个祖先节点就是 parent[x]。由于任意 k 可以分解为若干不同的 2 的幂(例如 13 = 8+4+1)，所以只需要预处理出这些 2^i 祖先节点，就可以快速地到达任意第 k 个祖先节点

例如 k = 13 = 8+4+1 = 1101_(2)，可以先往上跳 8 步，再往上跳 4步和1步;也可以先往上跳1步，再往上跳 4 步和 8 步。无论如何跳，都只需要跳 3 次就能到达第 13 个祖先节点据此，可以得到下面的算法。

算法：

在构造函数 TreeAncestor 中，预处理出每个节点 x 的第 2^i 个祖先节点，记作 pa[x][i] (若第 2^i 个祖先节点不存在则 pa[x][i] = -1) 。计算方式如下

先枚举 i，再枚举 x。相当于先算出所有爷爷节点，再算出所有爷爷的爷爷节点，依此类推.

pa[x][0]=parent[x]，即父节点。
pa[x][1]=pa[pa[x][0]][0]，即爷爷节点。
一般地，pa[x][i+1]=pa[pa[x][i]][i]。如果 pa[x][i] = -1 则 pa[x][1+1] = -1

这里 i+1至多为 logn 。例如 n = 13 时，log13 = 3，至多需要预处理到第 2^3 个祖先节点。 (当然，你也可以先把树高，或者每个节点的深度求出来，再据此做精细地计算。)

class TreeAncestor {private int[][] pa;public TreeAncestor(int n, int[] parent) {int m = 32 - Integer.numberOfLeadingZeros(n); // n 的二进制长度// 预处理出每个节点 x 的第 2^i 个祖先节点，记作 pa[x][i] pa = new int[n][m];for(int i = 0; i < n; i++){pa[i][0] = parent[i];}// 先枚举 `i`，再枚举 `x`。相当于先算出所有爷爷节点，再算出所有爷爷的爷爷节点，依此类推for(int i = 0; i < m-1; i++){for(int x = 0; x < n; x++){int p = pa[x][i];pa[x][i+1] = p < 0 ? -1 : pa[p][i];}}}public int getKthAncestor(int node, int k) {int m = 32 - Integer.numberOfLeadingZeros(k); // k 的二进制长度for(int i = 0; i < m; i++){if(((k >> i) & 1) > 0){ // k 的二进制从低到高第 i 位是 1node = pa[node][i];if(node < 0) break; // 如果node=-1, 说明第k个祖先节点不存在}}return node;}
}