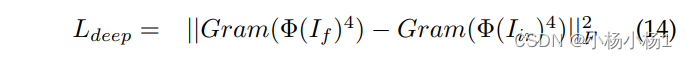【复杂网络建模】——ER网络和SF网络的阈值分析

1、介绍ER网络和SF网络

在复杂网络理论中，ER网络（Erdős-Rényi网络）和SF网络（Scale-Free网络）是两种常见的网络模型，它们在结构和特性上有很大的差异。分析它们的阈值涉及到不同的方法和概念。

ER网络（Erdős-Rényi网络）： ER网络是一种随机图模型，其中有N个节点，每对节点以概率p相连。ER网络的阈值分析通常涉及到一个相对简单的阈值，即当平均度（每个节点的平均连接数）超过某个阈值时，网络中就会出现一个巨大的联通成分，即基本上所有节点都可以彼此到达。这个阈值通常被称为临界点，表示为p_c。当平均度小于临界点时，网络中的联通成分较小，基本上是孤立的小群体。

SF网络（Scale-Free网络）： SF网络是一种特殊的网络，其度分布遵循幂律分布，意味着有少数节点具有非常高的度，而大多数节点具有较低的度。在SF网络中，没有明确的阈值，因为它们的结构不像ER网络那样简单。然而，可以通过一些度相关的指标来分析SF网络的特性，如平均最短路径长度、聚类系数和度相关的跳数。

在分析这两种网络的阈值时，主要的方法是通过数学模型、模拟和计算来研究网络中的连接模式、节点度分布、平均路径长度、聚类系数等特性。此外，可以使用一些图论和网络科学中的工具，例如计算平均度、度分布、节点间的距离等。对于ER网络，主要关注临界点，而对于SF网络，更关注度分布的幂律指数以及网络的规模等因素。

阈值分析的方法取决于网络模型的不同以及你感兴趣的特定网络属性。对于ER网络，重点是找到临界点，而对于SF网络，主要关注度分布和与度相关的特性。

2、计算网络阈值

2.1 ER（Erdős-Rényi）网络

使用 Python 中的 networkx 库生成 ER（Erdős-Rényi）网络，并计算其阈值。

import networkx as nx
import numpy as np# 创建 ER 网络
def generate_er_network(num_nodes, edge_probability):er_graph = nx.erdos_renyi_graph(num_nodes, edge_probability)return er_graph# 计算临界点阈值
def calculate_critical_threshold(num_nodes):return 1 / num_nodes# 参数设置
num_nodes = 100  # 节点数量
edge_probability = 0.1  # 节点间连接概率# 生成 ER 网络
er_network = generate_er_network(num_nodes, edge_probability)# 计算临界点阈值
critical_threshold = calculate_critical_threshold(num_nodes)# 打印临界点阈值和实际网络平均度
average_degree = np.mean(list(dict(er_network.degree()).values()))
print(f"临界点阈值: {critical_threshold}")
print(f"实际网络平均度: {average_degree}")

首先定义了一个用于生成 ER 网络的函数 generate_er_network，然后使用该函数创建了一个 ER 网络。接着，通过计算临界点阈值的函数 calculate_critical_threshold，计算了 ER 网络的临界点阈值。最后，通过计算实际网络平均度，打印出临界点阈值和实际网络平均度的值。

2.2 SF（Scale-Free）网络

首先定义了一个用于生成 SF 网络的函数 generate_sf_network，然后使用该函数创建了一个 SF 网络。接着，使用 networkx 提供的绘图函数绘制了网络图，并通过调用 plt.show() 进行显示。

import networkx as nx
import numpy as np
import matplotlib.pyplot as plt# 创建 SF 网络
def generate_sf_network(num_nodes, average_degree):sf_graph = nx.barabasi_albert_graph(num_nodes, int(average_degree/2))return sf_graph# 计算 SF 网络的阈值（在这里，SF 网络没有明确的阈值，这里只是一个示例）
def calculate_threshold(sf_network):# 这只是一个示例，SF 网络通常没有固定的阈值return np.mean(list(dict(sf_network.degree()).values()))# 参数设置
num_nodes = 100  # 节点数量
average_degree = 6  # 平均度# 生成 SF 网络
sf_network = generate_sf_network(num_nodes, average_degree)# 绘制网络图
pos = nx.spring_layout(sf_network)  # 布局
nx.draw(sf_network, pos, with_labels=False, node_size=50)
plt.title("Scale-Free Network")
plt.show()# 计算阈值（这里只是一个示例，实际上 SF 网络没有固定的阈值）
threshold = calculate_threshold(sf_network)
print(f"网络阈值: {threshold}")

网络可视化：

注意：不过SF 网络通常没有明确的阈值，因为其特点是度分布遵循幂律分布，没有临界点阈值。在示例代码中，计算阈值的函数只是一个示例，实际上 SF 网络没有固定的阈值。如果你想对 SF 网络进行更深入的分析，可能需要使用其他方法来探索其特性，如幂律指数等。

3、研究网络阈值的意义

在复杂网络理论中，研究网络阈值具有重要的意义，它涉及网络结构和功能之间的关系，有助于我们深入理解网络的行为和特性。以下是研究网络阈值的一些重要意义：

相变行为和临界现象理解：网络阈值通常与网络的相变行为和临界现象相关。相变是指网络从一种状态转变为另一种状态，如从无序到有序、从分散到集中。阈值是这种转变发生的临界点，研究它有助于理解网络的自组织、同步、相互作用等动态行为。

网络的强韧性和稳定性：网络阈值影响网络的强韧性和稳定性。在阈值之上，网络可能会迅速从分散的状态过渡到集中的状态，从而导致网络的强韧性下降。了解网络在不同条件下的阈值有助于预测网络在受到攻击、随机故障等情况下的行为。

网络设计和优化：研究网络阈值可以指导网络的设计和优化。不同的网络类型具有不同的阈值特性，根据所需的功能，可以调整网络参数以控制阈值，从而实现特定的网络性能和行为。

传播和扩散过程：阈值也与信息、疾病等在网络中的传播和扩散过程相关。在一些传播模型中，当节点的活跃邻居数达到一定阈值时，它可能会被激活。了解阈值有助于预测信息传播的速度和规模。

社会网络分析：在社交网络中，阈值可以解释为何某些节点更有可能成为影响力节点，即使其度数相对较低。这种影响力传播通常基于节点激活的阈值。

网络模型的验证：网络阈值可以用于验证不同的网络模型。比较模型生成的阈值与实际网络的阈值可以帮助我们了解模型的适用性和准确性。