二叉搜索树（C++）

二叉搜索树

  • 概念
  • 二叉搜索树的应用
  • 二叉搜索树的实现
    • K模型
      • 基本结构和函数声明
      • 接口实现
        • ①find——查找关键码
        • ②Insert——插入关键码
        • ③Erase——删除关键码（==重点==）
        • 时间复杂度
      • 源码（整体）
        • 非递归
        • 递归
    • KV模型

在使用C语言写数据结构阶段时，对二叉树进行了讲解。本节内容是对二叉树的深入探索，也是二叉树部分的收尾

概念

二叉搜索树也称二叉排序树（BST，Binary Search Tree）：

  1. 空树
  2. 非空树（要具有以下性质）
    • 若它的左子树不为空，则左子树上所有节点的值都小于根节点的值
    • 若它的右子树不为空，则右子树上所有节点的值都大于根节点的值
    • 它的左右子树也分别为二叉搜索树

注意： 二叉搜索树的key值互不相同

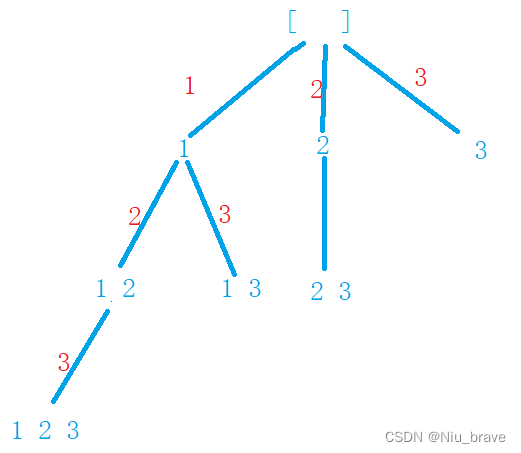
eg:下图就属于二叉搜索树
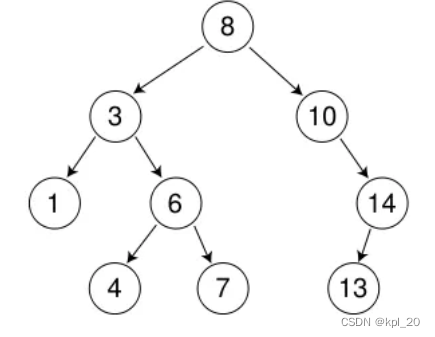
二叉搜索树

二叉搜索树的应用

  • K模型：即只有key作为关键码，结构中只需要存储key。关键码就是要搜索到的值

     eg: 给一个单词word，判断该单词是否拼写正确？具体步骤：1. 以词库中所有单词为基础，每个单词都是key，构建一颗搜索二叉树2. 在二叉树中搜索该单词是否存在，存在则返回true，否则返回false

  • KV模型：每一个关键码key，都有与之对应的value，即<Key, Value>的键值对

     eg1: 英汉词典 - 就是中文与英文的对应关系。通过英文可以快速找到与其对应的中文，英文单词和与其对应的中文<word, chinese>就构成键值对。eg2: 统计单词次数，统计成功后，给定单词就可以找到单词出现得次数。单词与其出现次数就是<word, count>就构成一种键值对

二叉搜索树的实现

注意： 通过二叉搜索树的应用，了解到其有两个模型，接下来对这两个模型分别进行实现。因为两个模型的接口都相似，所以仅对一个模型的接口进行详细介绍。

K模型

K模型的实现分为递归和非递归两种，但是接口的实现逻辑是一样的。为了便于理解把基本结构和函数声明先附上，然后对接口进行讲解，最后在贴上完整的源码

基本结构和函数声明

//二叉树节点
//节点使用struct，默认public访问
template<class K>
struct BSTreeNode   
{BSTreeNode<K>* _left;BSTreeNode<K>* _right;K _key;BSTreeNode(const K& key):_left(nullptr), _right(nullptr), _key(key){}
};template<class K>
class BSTree
{typedef BSTreeNode<K> Node;
public://默认构造BSTree():_root(nullptr){}//拷贝构造BSTree(const BSTree<K>& t);//赋值运算符重载BSTree<K>& operator=(BSTree<K> t);//析构函数~BSTree();//插入bool Insert(const K& key);//查找bool Find(const K& key);//删除bool Erase(const K& key);//中序遍历void InOrder();private:Node* _root;
};

接口实现

①find——查找关键码

功能：查找关键码是否在树中，是返回真，否则返回假。
原理：

  1. 从根开始比较，比根大则往右边查找，比根小往左边查找
  2. 最多查找高度次，走到nullptr，则这个值不存在

实现代码

  1. 非递归版本
template<class K>
bool BSTree<K>::Find(const K& key)
{Node* cur = _root;while (cur){if (cur->_key > key){cur = cur->_left;}else if (cur->_key < key){cur = cur->_right;}else{return true;}}return false;
}
  1. 递归版本
bool Find(const K& key)
{Node* cur = _root;while (cur){if (cur->_key > key){cur = cur->_left;}else if (cur->_key < key){cur = cur->_right;}else{return true;}}return false;
}

②Insert——插入关键码

原理：

  1. 树为空，直接把要插入的节点赋值给root
  2. 树不为空，通过查找的思路，找到要插入的合适位置。插入成功返回true
    注意：如果要插入的值和树中的值冲突，则返回false

实现代码

  1. 非递归版本
//插入
bool Insert(const K& key)
{if (_root == nullptr){_root = new Node(key);return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_key > key){parent = cur;cur = cur->_left;}else if (cur->_key < key){parent = cur;cur = cur->_right;}else{return false;}}cur = new Node(key);if (parent->_key > key){parent->_left = cur;}else{parent->_right = cur;}return true;
}
  1. 递归版本
bool InsertR(const K& key)
{return _InsertR(_root, key);
}
bool _FindR(Node* root, const K& key)
{if (root == nullptr)return false;if (root->_key > key)return _FindR(root->_left, key);else if (root->_key < key)return _FindR(root->_right, key);elsereturn true;
}

③Erase——删除关键码（重点）

原理：

  1. 查找关键码是否在二叉搜索树中，不存在直接返回false
  2. 存在，则要分为四种情况

情况：
在考虑树的所有情况时，要把根节点的情况和普通情况，分离开来。哪怕最后根节点的情况和普通情况一样。（仅代表博主个人观点）

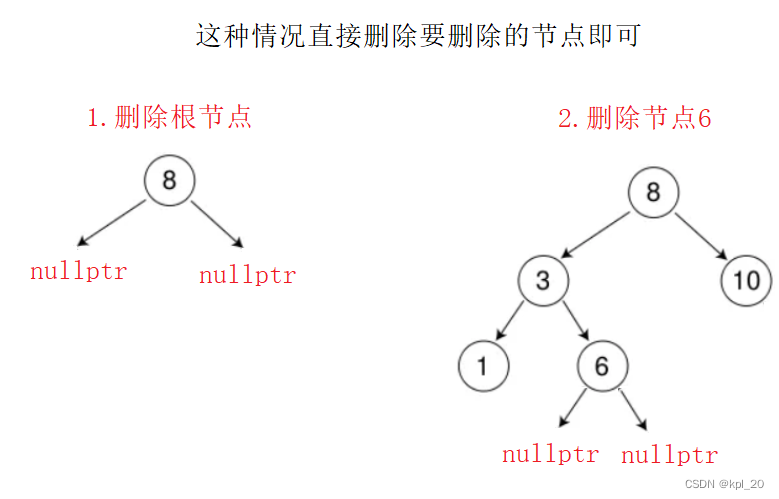
  1. 要删除的节点无孩子节点
    第一种情况
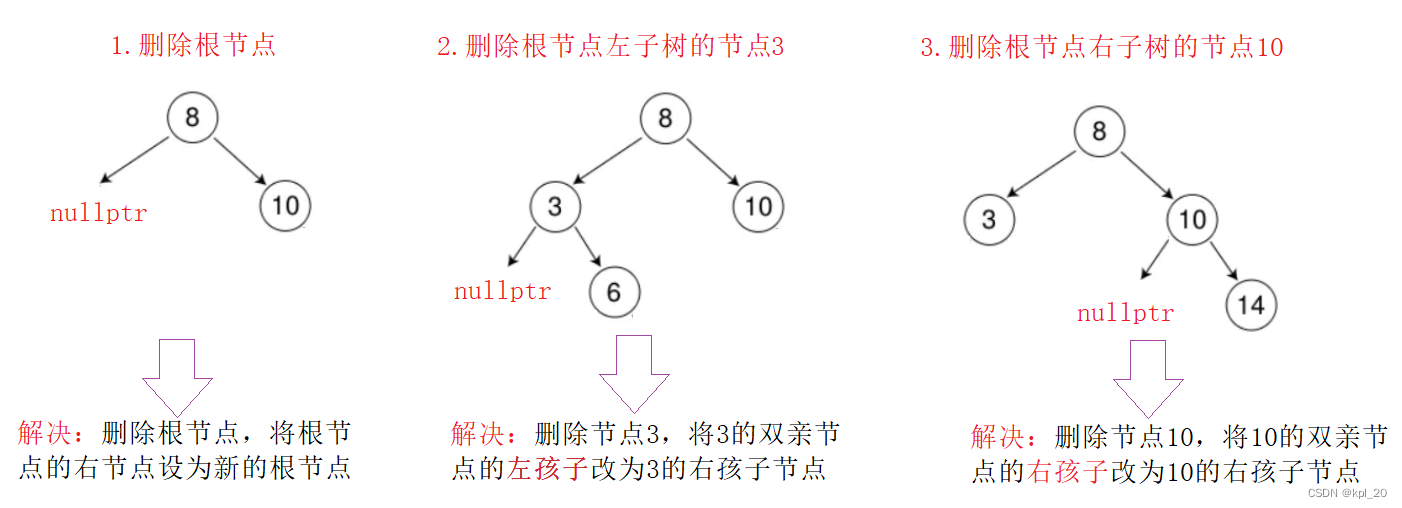
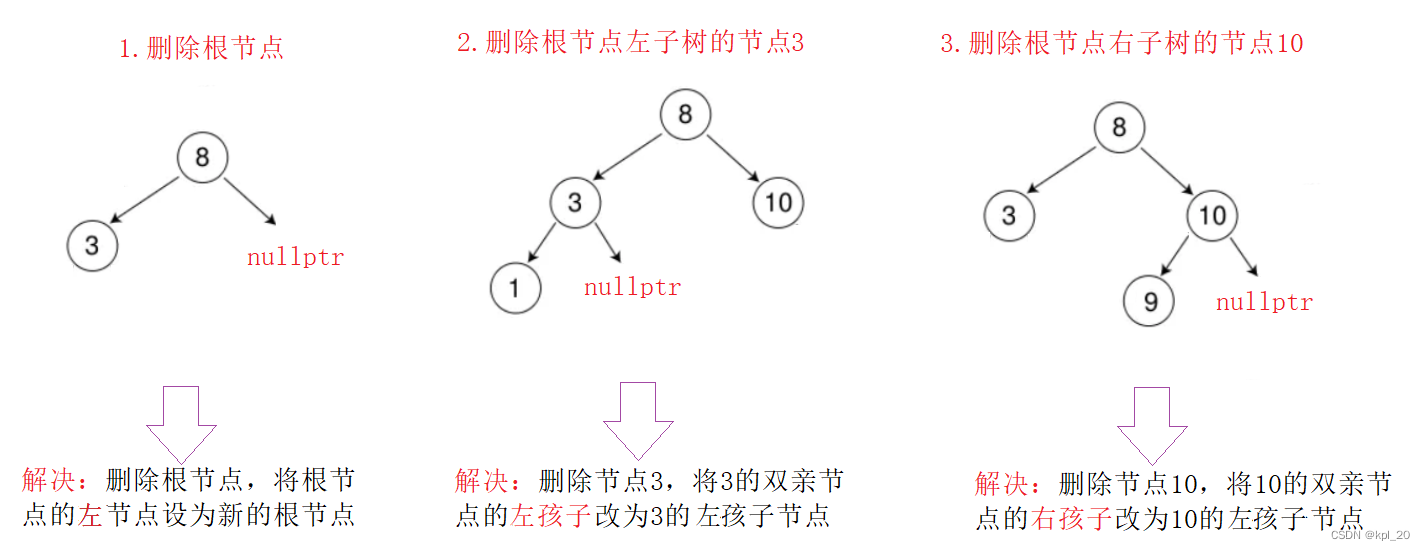
  1. 要删除的节点无左孩子节点
    第二种情况
  1. 要删除的节点无右孩子节点
    第三种情况
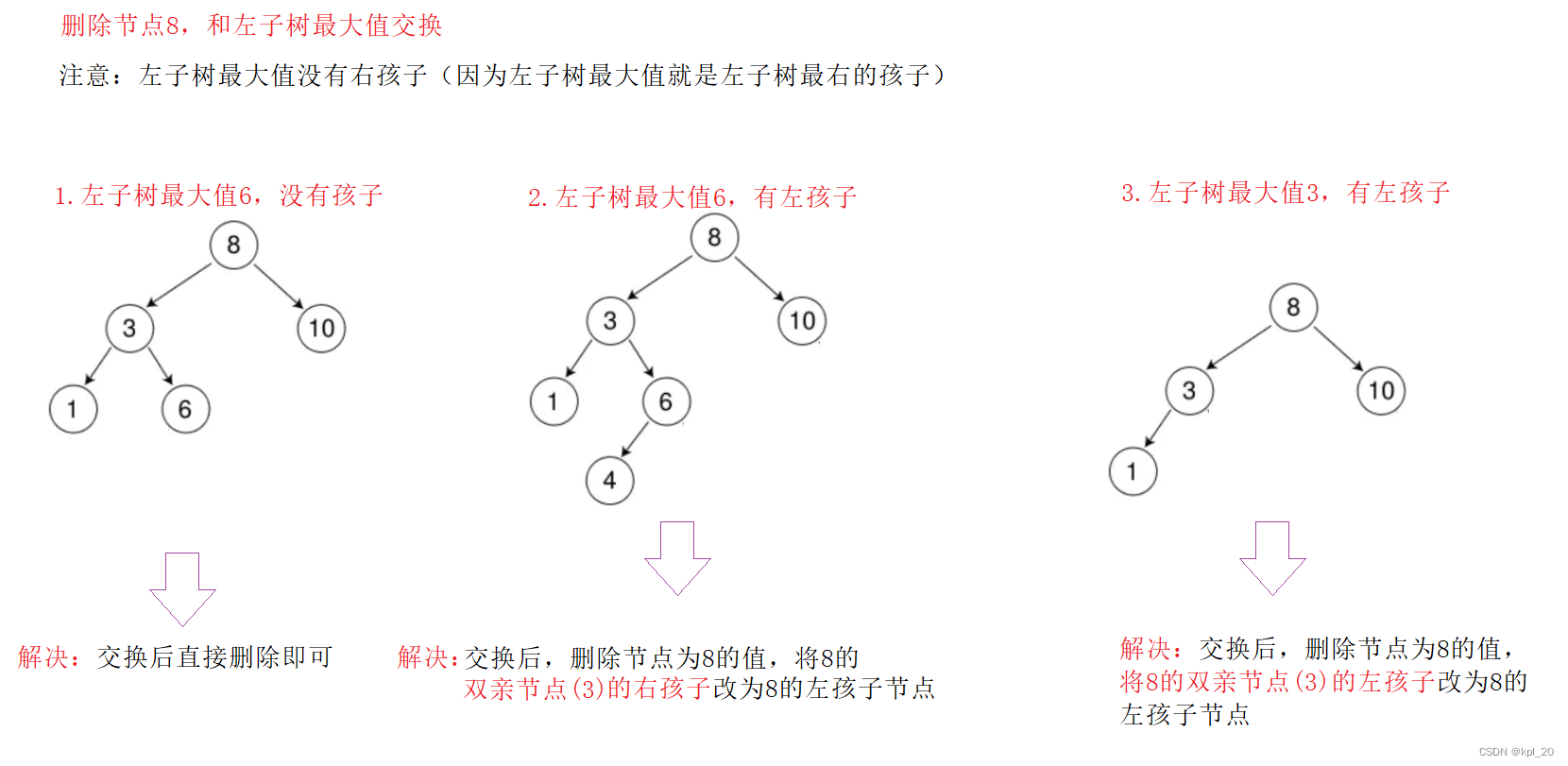
  1. 要删除的节点左右都不为空 （采用的方法 一 替换法）
    替换法：找到删除节点左子树的最大值节点(leftMax)，然后与删除节点交换，再删除现在的leftMax。（也可以找删除节点右子树的最小值节点(rightMin)，原理相同）
    第四种情况

实现代码

  1. 非递归版本
//删除
bool Erase(const K& key)
{Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_key > key){parent = cur;cur = cur->_left;}else if (cur->_key < key){parent = cur;cur = cur->_right;}else  //找到了要删除的值{//分情况//1.左为空if (cur->_left == nullptr){if (cur == _root)_root = cur->_right;else{if (parent->_right == cur){parent->_right = cur->_right;}else{parent->_left = cur->_right;}}}//2.右为空else if (cur->_right == nullptr){if (cur == _root)_root = cur->_left;else{if (parent->_right == cur){parent->_right = cur->_left;}else{parent->_left = cur->_left;}}} //3.左右都不为空else{parent = cur;Node* leftMax = cur->_left;while (leftMax->_right){parent = leftMax;leftMax = leftMax->_right;}swap(cur->_key, leftMax->_key);if (parent->_left == leftMax){parent->_left = leftMax->_left;}else{parent->_right = leftMax->_left;}cur = leftMax;}delete cur;cur = nullptr;return true;}}return false;
}
  1. 递归版本
//删除
bool EraseR(const K& key)
{return _EraseR(_root, key);
}bool _EraseR(Node*& root, const K& key)
{if (root == nullptr)return false;if (root->_key < key)return _EraseR(root->_right, key);else if (root->_key > key)return _EraseR(root->_left, key);else{Node* del = root;if (root->_left == nullptr)root = root->_right;else if (root->_right == nullptr)root = root->_left;else{Node* leftMax = root->_left;while (leftMax->_right){leftMax = leftMax->_right;}swap(root->_key, leftMax->_key);return _EraseR(root->_left, key);}delete del;del = nullptr;return true;}
}

时间复杂度

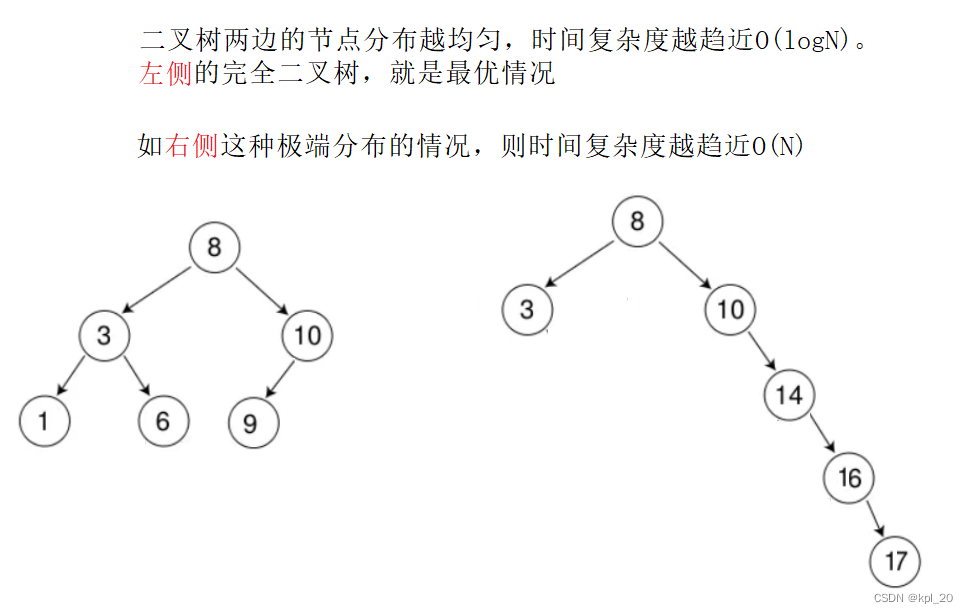
二叉搜索树的操作时间复杂度：在O(logN)和O(N)之间。
画图解释时间复杂度：
时间复杂度

源码（整体）

非递归

//非递归
namespace key
{//二叉树节点//节点使用struct，默认public访问template<class K>struct BSTreeNode{BSTreeNode<K>* _left;BSTreeNode<K>* _right;K _key;BSTreeNode(const K& key):_left(nullptr), _right(nullptr), _key(key){}};template<class K>class BSTree{typedef BSTreeNode<K> Node;public://默认构造BSTree():_root(nullptr){}//拷贝构造BSTree(const BSTree<K>& t){_root = Copy(t._root);}//赋值运算符重载BSTree<K>& operator=(BSTree<K> t){swap(_root, t._root);return *this;}//析构函数~BSTree(){Destroy(_root);}//插入bool Insert(const K& key){if (_root == nullptr){_root = new Node(key);return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_key > key){parent = cur;cur = cur->_left;}else if (cur->_key < key){parent = cur;cur = cur->_right;}else{return false;}}cur = new Node(key);if (parent->_key > key){parent->_left = cur;}else{parent->_right = cur;}return true;}//查找bool Find(const K& key){Node* cur = _root;while (cur){if (cur->_key > key){cur = cur->_left;}else if (cur->_key < key){cur = cur->_right;}else{return true;}}return false;}//删除bool Erase(const K& key){Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_key > key){parent = cur;cur = cur->_left;}else if (cur->_key < key){parent = cur;cur = cur->_right;}else  //找到了要删除的值{//分情况//1.左为空if (cur->_left == nullptr){if (cur == _root)_root = cur->_right;else{if (parent->_right == cur){parent->_right = cur->_right;}else{parent->_left = cur->_right;}}}//2.右为空else if (cur->_right == nullptr){if (cur == _root)_root = cur->_left;else{if (parent->_right == cur){parent->_right = cur->_left;}else{parent->_left = cur->_left;}}} //3.左右都不为空else{parent = cur;Node* leftMax = cur->_left;while (leftMax->_right){parent = leftMax;leftMax = leftMax->_right;}swap(cur->_key, leftMax->_key);if (parent->_left == leftMax){parent->_left = leftMax->_left;}else{parent->_right = leftMax->_left;}cur = leftMax;}delete cur;cur = nullptr;return true;}}return false;}//中序遍历void InOrder(){_InOrder(_root);cout << endl;}private:Node* Copy(Node* root){if (root == nullptr)return nullptr;Node* copyRoot = new Node(root->_key);copyRoot->_left = Copy(root->_left);copyRoot->_right = Copy(root->_tight);return copyRoot;}void Destroy(Node*& root){if (root == nullptr)return;Destroy(root->_left);Destroy(root->_right);delete root;root = nullptr;}void _InOrder(Node* root){if (root == nullptr)return;_InOrder(root->_left);cout << root->_key << " ";_InOrder(root->_right);}private:Node* _root;};
}

递归

//递归
namespace keyR
{//二叉树节点//节点使用struct，默认public访问template<class K>struct BSTreeNode{BSTreeNode<K>* _left;BSTreeNode<K>* _right;K _key;BSTreeNode(const K& key):_left(nullptr), _right(nullptr), _key(key){}};template<class K>class BSTree{typedef BSTreeNode<K> Node;public://默认构造BSTree():_root(nullptr){}//拷贝构造BSTree(const BSTree<K>& t){_root = Copy(t._root);}//赋值运算符重载BSTree<K>& operator=(BSTree<K> t){swap(_root, t._root);return *this;}//析构函数~BSTree(){Destroy(_root);}//插入bool InsertR(const K& key){return _InsertR(_root, key);}//查找bool FindR(const K& key){return _FindR(_root, key);}//删除bool EraseR(const K& key){return _EraseR(_root, key);}//中序遍历void InOrder(){_InOrder(_root);cout << endl;}private://在root添加引用很关键，要不然得是二级指针bool _InsertR(Node*& root, const K& key){if (root == nullptr){root = new Node(key);return true;}if (root->_key > key)return _InsertR(root->_left, key);else if (root->_key < key)return _InsertR(root->_right, key);elsereturn false;}bool _EraseR(Node*& root, const K& key){if (root == nullptr)return false;if (root->_key < key)return _EraseR(root->_right, key);else if (root->_key > key)return _EraseR(root->_left, key);else{Node* del = root;if (root->_left == nullptr)root = root->_right;else if (root->_right == nullptr)root = root->_left;else{Node* leftMax = root->_left;while (leftMax->_right){leftMax = leftMax->_right;}swap(root->_key, leftMax->_key);return _EraseR(root->_left, key);}delete del;del = nullptr;return true;}}bool _FindR(Node* root, const K& key){if (root == nullptr)return false;if (root->_key > key)return _FindR(root->_left, key);else if (root->_key < key)return _FindR(root->_right, key);elsereturn true;}void Destroy(Node*& root){if (root == nullptr)return;Destroy(root->_left);Destroy(root->_right);delete root;root = nullptr;}Node* Copy(Node* root){if (root == nullptr)return nullptr;Node* copyRoot = new Node(root->_key);copyRoot->_left = CopyRoot(root->_left);copyRoot->_right = CopyRoot(root->_right);return copyRoot;}void _InOrder(Node* root){if (root == nullptr)return;_InOrder(root->_left);cout << root->_key << " ";_InOrder(root->_right);}private:Node* _root;};
}

KV模型

直接贴出源码：

namespace key_value
{template<class K, class V>struct BSTreeNode{BSTreeNode<K, V>* _left;BSTreeNode<K, V>* _right;K _key;V _value;BSTreeNode(const K& key, const V& value):_left(nullptr), _right(nullptr), _key(key), _value(value){}};template<class K, class V>class BSTree{typedef BSTreeNode<K, V> Node;public:BSTree():_root(nullptr){}BSTree(const BSTree<K, V>& t){_root = Copy(t._root);}BSTree<K, V>& operator=(BSTree<K, V> t){swap(_root, t._root);return *this;}~BSTree(){Destroy(_root);}void InOrder(){_InOrder(_root);cout << endl;}Node* FindR(const K& key){return _FindR(_root, key);}bool InsertR(const K& key, const V& value){return _InsertR(_root, key, value);}bool EraseR(const K& key){return _EraseR(_root, key);}private:bool _EraseR(Node*& root, const K& key){if (root == nullptr)return false;if (root->_key < key){return _EraseR(root->_right, key);}else if (root->_key > key){return _EraseR(root->_left, key);}else{Node* del = root;if (root->_left == nullptr){//这个root的引用，非常好，root = root->_right;}else if (root->_right == nullptr){root = root->_left;}else{Node* leftMax = root->_left;while (leftMax->_right){leftMax = leftMax->_right;}swap(root->_key, leftMax->_key);//删的值在左边return _EraseR(root->_left, key);}delete del;return true;}}void Destroy(Node*& root){if (root == nullptr)return;Destroy(root->_left);Destroy(root->_right);delete root;root = nullptr;}Node* Copy(Node* root){if (root == nullptr)return nullptr;Node* copyRoot = new Node(root->_key, root->_value);copyRoot->_left = Copy(root->_left);copyRoot->_right = Copy(root->_right);return copyRoot;}void _InOrder(Node* root){if (root == nullptr)return;_InOrder(root->_left);cout << root->_key << ":" << root->_value << endl;_InOrder(root->_right);}Node* _FindR(Node* root, const K& key){if (root == nullptr)return nullptr;if (root->_key > key){return _FindR(root->_left, key);}else if (root->_key < key){return _FindR(root->_right, key);}else{return root;}}bool _InsertR(Node*& root, const K& key, const V& value){if (root == nullptr){root = new Node(key, value);return true;}if (root->_key > key){return _InsertR(root->_left, key, value);}else if (root->_key < key){return _InsertR(root->_right, key, value);}else{return false;}}private:Node* _root;};}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.rhkb.cn/news/111785.html

如若内容造成侵权/违法违规/事实不符，请联系长河编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

安防监控/视频汇聚平台EasyCVR调用rtsp地址返回的IP不正确是什么原因？

安防监控/视频汇聚平台EasyCVR调用rtsp地址返回的IP不正确是什么原因？

安防监控/云存储/磁盘阵列存储/视频汇聚平台EasyCVR可拓展性强、视频能力灵活、部署轻快&#xff0c;可支持的主流标准协议有GB28181、RTSP/Onvif、RTMP等&#xff0c;以及厂家私有协议与SDK接入&#xff0c;包括海康Ehome、海大宇等设备的SDK等&#xff0c;能对外分发RTSP、RT…
阅读更多...
Linux系统下vim常用命令

Linux系统下vim常用命令

一、基础命令&#xff1a; v:可视模式 i:插入模式 esc:命令模式下 :q &#xff1a;退出 :wq &#xff1a;保存并退出 ZZ&#xff1a;保存并退出 :q! &#xff1a;不保存并强制退出二、在Esc下&#xff1a; dd : 删除当前行 yy:复制当前行 p:复制已粘贴的文本 u:撤销上一步 U:…
阅读更多...
【【萌新的STM32-22中断概念的简单补充】】

【【萌新的STM32-22中断概念的简单补充】】

萌新的STM32学习22-中断概念的简单补充 我们需要注意的是这句话 从上面可以看出&#xff0c;STM32F1 供给 IO 口使用的中断线只有 16 个&#xff0c;但是 STM32F1 的 IO 口却远远不止 16 个&#xff0c;所以 STM32 把 GPIO 管脚 GPIOx.0~GPIOx.15(xA,B,C,D,E,F,G)分别对应中断…
阅读更多...
Pillow：Python的图像处理库（安装与使用教程）

Pillow：Python的图像处理库（安装与使用教程）

在Python中&#xff0c;Pillow库是一个非常强大的图像处理库。它提供了广泛的图像处理功能&#xff0c;让我们可以轻松地操作图像&#xff0c;实现图像的转换、裁剪、缩放、旋转等操作。此外&#xff0c;Pillow还支持多种图像格式的读取和保存&#xff0c;包括JPEG、PNG、BMP、…
阅读更多...
【已解决】ZooKeeper配置中出现Error contacting service. It is probably not running

【已解决】ZooKeeper配置中出现Error contacting service. It is probably not running

ZooKeeper配置中出现Error contacting service. It is probably not running 问题 安装zookeeper&#xff0c;启动报错了 Error contacting service. It is probably not running 思路 tail -100f logs/zookeeper-root-server-node1.itcast.cn.out 查看日志报错 zoo.cfg没…
阅读更多...
FPGA VR摄像机-拍摄和拼接立体 360 度视频

FPGA VR摄像机-拍摄和拼接立体 360 度视频

本文介绍的是 FPGA VR 相机的第二个版本&#xff0c;第一个版本是下面这样&#xff1a; 第一版地址&#xff1a; ❝ https://hackaday.io/project/26974-vr-camera-fpga-stereoscopic-3d-360-camera ❞ 本文主要介绍第二版本&#xff0c;第二版本的 VR 摄像机&#xff0c;能够以…
阅读更多...
使用 Privoxy 在 Linux 上配置本地代理服务器详细教程

使用 Privoxy 在 Linux 上配置本地代理服务器详细教程

Privoxy 是一个功能强大的开源网络代理软件&#xff0c;它可以帮助我们在 Linux 系统上搭建本地代理服务器。通过配置和使用 Privoxy&#xff0c;您可以实现更安全、匿名以及自定义过滤规则等高级特性。本文将详细介绍如何在 Linux 环境下利用 Privoxy 配置并运行本地代理服务器…
阅读更多...
递归算法学习——子集

递归算法学习——子集

目录 一&#xff0c;题目解析 二&#xff0c;例子 三&#xff0c;题目接口 四&#xff0c;解题思路以及代码 1.完全深度搜索 2.广度搜索加上深度优先搜索 五&#xff0c;相似题 1.题目 2.题目接口 3.解题代码 一&#xff0c;题目解析 给你一个整数数组 nums &#xff0c…
阅读更多...
拼多多anti-token分析

拼多多anti-token分析

前言&#xff1a;拼多多charles抓包分析发现跟商品相关的请求头里都带了一个anti-token的字段且每次都不一样,那么下面的操作就从分析anti-token开始了 1.jadx反编译直接搜索 选中跟http相关的类对这个方法进行打印堆栈 结合堆栈方法调用的情况找到具体anti-token是由拦截器类f…
阅读更多...
C语言每日一练------Day(5)

C语言每日一练------Day(5)

本专栏为c语言练习专栏&#xff0c;适合刚刚学完c语言的初学者。本专栏每天会不定时更新&#xff0c;通过每天练习&#xff0c;进一步对c语言的重难点知识进行更深入的学习。 今日练习题关键字&#xff1a;错误的集合 密码检查 &#x1f493;博主csdn个人主页&#xff1a;小小u…
阅读更多...
系统架构：软件工程

系统架构：软件工程

文章目录 资源知识点自顶向下与自底向上形式化方法结构化方法敏捷方法净室软件工程面向服务的方法面向对象的方法快速应用开发螺旋模型软件过程和活动开放式源码开发方法功用驱动开发方法统一过程模型RUP基于构件的软件开发UML 资源 信息系统开发方法 知识点 自顶向下与自底…
阅读更多...
QtConcurrent和QFuture的使用

QtConcurrent和QFuture的使用

在Qt中&#xff0c;有时候我们会遇到这样一种情况&#xff0c;需要执行一个很长时间的操作&#xff0c;这时候我们的主界面就会卡住。我们的通常做法就是把这个很长时间的操作扔到线程里去处理&#xff0c;可以使用标准库中的线程也可以使用QThread。 如果我们要在这个很长时间…
阅读更多...
ChatGPT 随机动态可视化图表分析

ChatGPT 随机动态可视化图表分析

动态可视化图表分析实例如下图： 这样的动态可视化图表可以使用ChatGPT OpenAI 来实现。 给ChatGPT发送指令： 你现在是一个数据分析师，请使用HTML，JS，Echarts，来完成一个动态条形图，条形图方向横向，数据可以随机生成，并且随机生成10个不同的商品名称，每个类别分别用…
阅读更多...
Nginx到底是什么，他能干什么？

Nginx到底是什么，他能干什么？

目录 Ngnix是什么&#xff0c;它是用来做什么的呢&#xff1f; 一。Nginx简介 二&#xff0c;为什么要用Nginx呢&#xff1f; 二。Nginx应用 1.HTTP代理和反向代理 2.负载均衡 Ngnix是什么&#xff0c;它是用来做什么的呢&#xff1f; 一。Nginx简介 Nginx是enginex的简写&…
阅读更多...
基于大语言模型知识问答应用落地实践 – 知识库构建（下）

基于大语言模型知识问答应用落地实践 – 知识库构建（下）

上篇介绍了构建知识库的大体流程和一些优化经验细节&#xff0c;但并没有结合一个具体的场景给出更细节的实战经验以及相关的一些 benchmark 等&#xff0c;所以本文将会切入到一个具体场景进行讨论。 目标场景&#xff1a;对于 PubMed 医疗学术数据中的 1w 篇文章进行知识库构…
阅读更多...
Mycat之前世今生

Mycat之前世今生

如果我有一个32核心的服务器&#xff0c;我就可以实现1个亿的数据分片&#xff0c;我有32核心的服务器么&#xff1f;没有&#xff0c;所以我至今无法实现1个亿的数据分片。——MyCAT ‘s Plan 话说“每一个成功的男人背后都有一个女人”&#xff0c;自然MyCAT也逃脱不了这个诅…
阅读更多...
C语言每日一练------Day(6)

C语言每日一练------Day(6)

本专栏为c语言练习专栏&#xff0c;适合刚刚学完c语言的初学者。本专栏每天会不定时更新&#xff0c;通过每天练习&#xff0c;进一步对c语言的重难点知识进行更深入的学习。 今日练习题关键字&#xff1a;整数转换 异或 &#x1f493;博主csdn个人主页&#xff1a;小小unicorn…
阅读更多...
ChatGPT⼊门到精通(2):ChatGPT 能为我们做什么

ChatGPT⼊门到精通(2):ChatGPT 能为我们做什么

⼀、雇佣免费的⼲活⼩弟 有了ChatGPT后&#xff0c;就好⽐你有了好⼏个帮你免费打⼯的「⼩弟」&#xff0c;他们可以帮你做很多 ⼯作。我简单总结⼀些我⽬前使⽤过的⽐较好的基于ChatGPT的服务和应⽤。 1、总结、分析 当我们在阅读⼀些⽂章和新闻的时候&#xff0c;有的⽂章写…
阅读更多...
ARM-M0 + 24bit 高精度ADC，采样率4KSPS，国产新品，传感器首选

ARM-M0 + 24bit 高精度ADC，采样率4KSPS，国产新品，传感器首选

ARM-M0内核MCU 内置24bit ADC &#xff0c;采样率4KSPS flash 64KB&#xff0c;SRAM 32KB 适用于传感器&#xff0c;电子秤&#xff0c;体脂秤等等
阅读更多...
同源策略与解决方法

同源策略与解决方法

同源策略与解决方法 1.浏览器的同源策略 1.1 同源策略 同源策略&#xff08;same origin policy&#xff09;&#xff0c;一种安全策略&#xff0c;用于限制一个源的文档或者它加载的脚本如何能与另一个源的资源进行交互。 浏览器默认两个不同的源之间是可以互相访问资源和…
阅读更多...
最新文章
推荐文章

Copyright @ 2022~2023